Постоянная функция

ИССЛЕДОВАНИЕ ФУНКЦИЙ

РЕФЕРАТ

Студент гр. 524

______________ Т. Ю. Яковлева

Проверил преподаватель

______________ Н. Ф. Баранник

Томск 2014

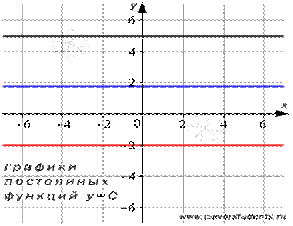
Постоянная функция.

y=C, где C – некоторое действительное число.

Пример: y=5, y=-2 и y=√3.

Свойства постоянной функции:

1. Область определения: все множество действительных чисел.
2. Постоянная функция является четной.
3. Область значений: множество, состоящее из единственного числа С.
4. Постоянная функция невозрастающая и неубывающая.
5. Асимптот нет.
6. Функция проходит через точку (0,C) координатной плоскости.

Корень n -ой степени.

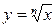, где n – натуральное число, большее единицы.

Корень n -ой степени, n - четное число.

Пример: .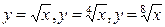

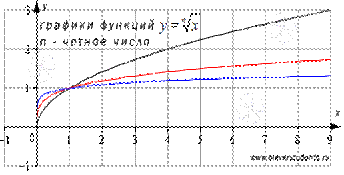
Свойства функции корень n -ой степени при четных n:

1. Область определения: множество всех неотрицательных действительных чисел .
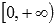2. При x=0 функция 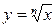принимает значение, равное нулю.
3. Функция не является четной или нечетной.
4. Область значений функции: .
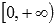5. Функция 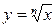при четных показателях корня возрастает на всей области определения.
6. Эта функция имеет выпуклость, направленную вверх, на всей области определения, точек перегиба нет.
7. Асимптот нет.
8. График функции корень n -ой степени при четных n проходит через точки (0,0) и (1,1).

Корень n -ой степени, n - нечетное число.

Пример: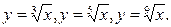

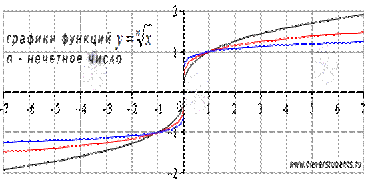
Свойства функции корень n -ой степени при нечетных n:

1. Область определения: множество всех действительных чисел.

2. Функция нечетная.

3. Область значений функции: множество всех действительных чисел.

4. Функция 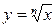при нечетных показателях корня возрастает на всей области определения.

5. Эта функция вогнутая на промежутке 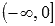и выпуклая на промежутке 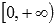, точка с координатами (0,0) – точка перегиба.

6. Асимптот нет.

7. График функции корень n -ой степени при нечетных n проходит через точки (-1,-1), (0,0) и (1,1).