Элементы теории корреляции и регрессионного анализа

Если в результате осуществления некоторого эксперимента наблюдаются две величины 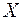и 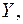то выборочный корреляционный момент 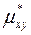величин 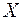и 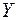определяется формулой

,

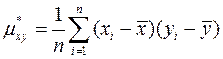где 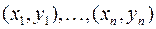– 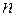пар значений, полученных в 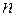независимых повторениях эксперимента,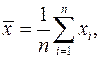

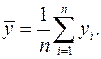
Выборочный коэффициент корреляции 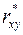равен

,

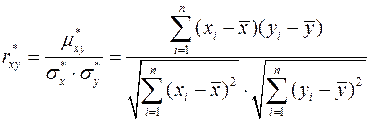где , .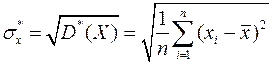

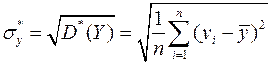Выборочный коэффициент регрессии 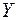на

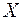
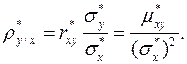
Выборочный коэффициент регрессии 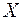на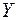

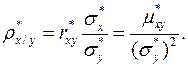
Выборочное уравнение регрессии 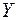на 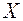имеет вид

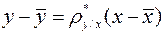или .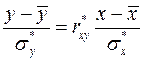

Выборочное уравнение регрессии 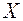на :

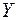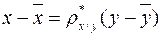или .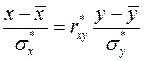

Задачи

15.1. Найти коэффициент корреляции и уравнения регрессии X на Y и Y на X:

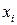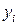15.2. Экспериментально получено 5 точек с координатами: (1; 4,3),(2; 5,3), (3; 3,8), (4; 1,8), (5; 2,3). Найти коэффициент корреляциии уравнения линий регрессии Y на X и X на Y.

15.3. Составить регрессии X на Y и Y на X:

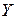	Х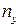
-3	-2	-1
-2
-1

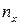15.4. Предел выносливости стали при изгибе Y (в Н/мм²) оценивается на основании другой её характеристики – предела упругости при кручении X (в Н/мм²). Результаты измерений:

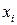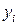По опытным данным для 12 марок стали вычислить коэффициент корреляции между этими характеристиками и найти уравнения линейной регрессии Y на X и X на Y.

15.5. По данным измерений двух переменных:

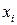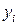Вычислить коэффициент корреляции и найти уравнение линейной регрессии Y на X.

15.6. Растворимость (в 100 частях воды) азотнокислого натрия NaNO3 в зависимости от температуры t представлена в таблице:

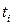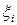	66,7		76,3	80,6	85,7	92,9	99,4	113,6	125,1

Через 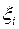обозначено количество NaNO3 (в условных частях). Найти линейную зависимость 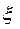от t.

15.7. Для изучения зависимости урожайности Y (в ц/га) от количества X внесённых удобрений (в т/га) проведено 10 наблюдений над контрольными участками посева. Результаты собраны в таблице:

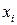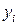а)Построить диаграмму рассеивания;

б)Найти уравнение прямой регрессии Y на X, изобразить её на диаграмме рассеивания;

в)Какую урожайность следует ожидать при внесении 5 и 13 т/га удобрений?

15.8. Для исследования зависимости между длиной ампул X (в мм) и её объёмом Y (в см³) произведена случайная бесповторная выборка 10 ампул.

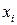	1,0	1,1	0,9	1,0	1,1	1,2	1,3	1,1	1,0	1,0
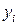	19,5	19,0	18,3	20,0	20,8	23,0	25,2	19,6	21,0	19.5

Статистическими методами изучить зависимость между случайными величинами X и Y; составить уравнение прямой регрессии Y на X, изобразить её на диаграмме рассеивания.

15.9. На 10 предприятиях исследовалась зависимость среднемесячной выработки продукции Y (в тыс. руб.) на одного рабочего от стоимости X (в млн. руб.) основных средств производства:

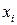	0,8	0,9	0,9	1,0	1,0	1,1	1,0	1,2	1,2	1,3
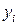	9,9	10,1	10,2	10,2	10,1	10,2	10,4	10,4	10,5	10,5

Составить уравнения прямых регрессии Y на X и X на Y.

15.10. Найти выборочное уравнение регрессии 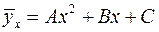по данным, приведённым в следующей корреляционной таблице:

		-	-
	-
	-

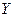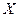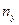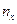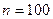15.11. Найти выборочное уравнение прямой линии регрессии 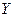на 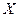по данным, приведённым в следующей таблице:

			-	-	-
	-			-	-
	-	-
	-	-
	-	-	-

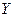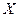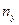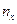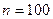Литература

1. Бочаров, П.П. Теория вероятностей. Математическая статистика: учебник для вузовов / П.П. Бочаров, А.В. Печинкин. – М.: Высшая школа, 1999.

2. Бугров, Я.С. Краткий курс теории вероятностей и математической статистики: учебник для вузов / Я.С. Бугров, С. М. Никольский. – М.: Наука, 1987.

3. Вентцель, А.С. Теория вероятностей и математическая статистика: учебник для вузов / Е.С. Вентцель. – М.: Высшая школа, 2002.

4. Гмурман, В.Е. Теория вероятностей и математическая статистика: учеб. пособие для втузов / В.Е. Гмурман. – М.: Высшая школа, 1999.

5. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В.Е. Гмурман. – М.: Высшая школа, 2002.

6. Кремер, Н.К. Теория вероятностей и математическая статистика: учеб. для вузов / Н.Ш. Кремер. – М.: ЮНИТИ-ДАНА, 2004.

7. Кочетков, В.Е. Краткий курс высшей математики: учебник для вузов / В.Е. Кочетков. – М.: РИЦ МГИУ, 2000.

8. Письменный, Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам: учеб.пособие / Д. Т. Письменный. – М.: Айрис-Пресс, 2008.

9. Сборник задач по высшей математике. 2 курс: учеб. пособие для вузов / К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко, Е.Д. Куланин, С.Н. Федин. – М.: Айрис-Пресс, 2007.

10. Чудесенко, В.Ф. Сборник заданий по специальным курсам высшей математики. Типовые расчеты: учеб. пособие / В.Ф Чудесенко. – СПб.: Лань, 2005. – 124 с.

Учебное издание

Батранина Марина Алексеевна

Якушина Светлана Ивановна