Примеры. №1. Найти частные производные функций

№1. Найти частные производные функций:

а) ;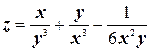

б) ;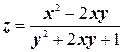

в) .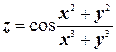

Решение.

а) Частные производные функции двух и более переменных определяются по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если по одной переменной дифференцируем, то остальные считаются постоянными.

Имеем: (напомним, что ):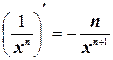

;

.

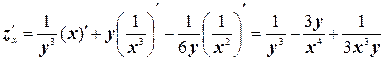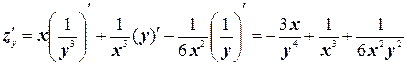б) Воспользуемся правилом дифференцирования дроби:

;

.

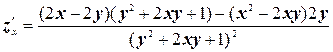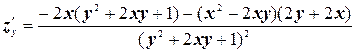в) Здесь имеем дело с производными сложной функции и дроби.

.

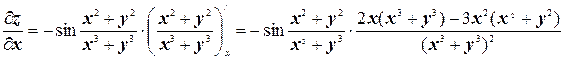Ввиду симметрии выражения 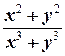относительно х и у можно записать сразу

.

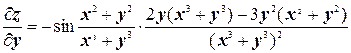№2. Найти полный дифференциал функций:

а) ;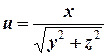

б) .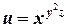

Решение.

а) Так как 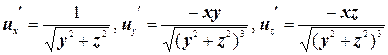, то полный дифференциал имеет вид .

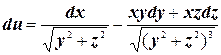б) Вычислим частные производные по х, у, z

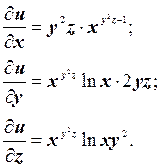
Таким образом, полный дифференциал

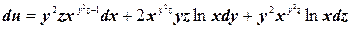
Варианты заданий

№4.1. Найти частные производные, частные дифференциалы данных функций по каждой из независимых переменных (x, y, z, t, …) и полный дифференциал:

а) ;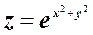

б) ;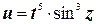

в) ;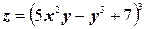

г) ;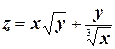

д) ;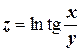

е) ;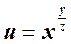

ж) ;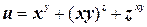

з) ;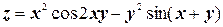

и) ;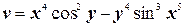

к) .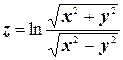

Контрольные вопросы