3.1 Комплексные числа
Для расчёта электрических цепей переменного тока с применением комплексных чисел необходимо знать формы их выражения. Алгебраическая форма имеет вид:
А = а + jb (3.1)
где а – вещественная часть, b– мнимая часть,j = 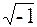 – мнимая единица.
– мнимая единица.
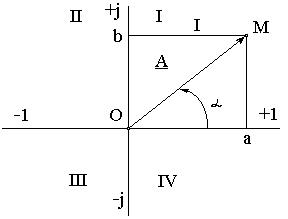 Комплексное число можно показать на комплексной плоскости как вектор, конец которого имеет координаты а и b (рисунок 3.1). По горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые.
Комплексное число можно показать на комплексной плоскости как вектор, конец которого имеет координаты а и b (рисунок 3.1). По горизонтальной оси откладываются вещественные числа, а по вертикальной – мнимые.
Рисунок 3.1
Длина отрезка ОМ в определённом масштабе определяет абсолютное значение или модуль комплексного числа:
A = 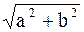
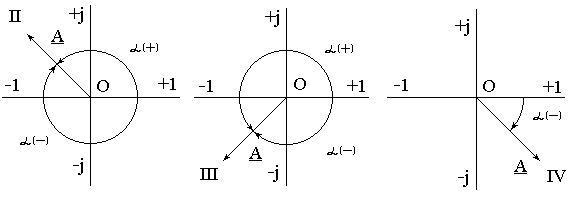
а) б) в)
Рисунок 3.2
Формула для определения угла α зависит от квадранта, в котором находится вектор комплексного числа. Угол α откладывается в положительном направлении против часовой стрелки, а в отрицательном направлении - по часовой стрелке от вещественной положительной оси. Это можно показать на рис. 3.2 (а, б и в).
Поскольку при расчёте угла α учащиеся зачастую допускают ошибки, формулы для его определения можно свести в таблицу 3.1. в которой также указываются знаки вещественной и мнимой частей в зависимости от квадранта, в котором находится заданный комплекс.
Если в формулу (3.1) подставить выражения a = A * Cos aи b = A * Sina, то получаем тригонометрическую форму выражения комплексного числа:
Таблица 3.1
| №№ квадрантов | Знаки вещественной и мнимой частей | Формулы для определения угла | |
| a | b | ||
| I | + | + | arc tg b/a |
| II | – | + | 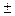 180° + arc tg b/a 180° + arc tg b/a |
| III | – | – | 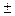 180° + arc tg b/a 180° + arc tg b/a |
| IV | + | – | arc tg b/a |
A = A * Cos α + jA * Sin α = A (Cos α + j Sin α).
В математике доказывается, что Cos α + j Sin α = ejα.
Тогда комплексное число можно выразить в показательной форме:
A = A * ejα.
Таким образом, комплексное число можно представить в виде:
A =a + jb= A (Cos α + j Sin α)= A * ejα. (3.2)
Комплексное число A =a – jb = A (Cos α – j Sin α) = A * ejα называется сопряжённым. Действия с комплексными числами выполняются так же, как действия с алгебраическими выражениями. Наиболее удобными для расчётов в комплексной форме являются микрокалькуляторы: SR-135 "CITIZEN"; SC-503 "CEDAR"; SC-105 "SHARP" и другие, подобные им по содержанию расширенной клавиатуры, имеющие специальный режим работы с комплексными числами, включаемый клавишами <Shift> или <2nd> + <CPLX>.
Действия с комплексными числами на этих калькуляторах выполняются в алгебраической форме. Однако они позволяют переводить комплекс из алгебраической формы в показательную и наоборот.
Например, переведём комплекс А = 3 – j4 в показательную форму, для этого используем тест: <Shift>, <CPLX>, <3>, <а>, <4>, <+/->, <b>, <Shift>, <a> (получаем модуль А=5), <b> (получаем угол α = –53,13°), то есть A = 3 – j4 = 5 * e-j53,13.
Для обратного перевода из показательной формы в алгебраическую применяется тест: <5>, <a>, <53,13>, <+/->, <b>, <Shift>, <a>,– (получаем вещественную часть а = 3), <b>,– (получаем мнимую часть b =–4). При этом клавиша <DRG> должна быть в положении <DEG>, которое индицируется на табло калькулятора.
Расчёты можно выполнять и на отечественных программируемых микрокалькуляторах типа МК-54, МК-56 и др.
Программ для расчёта с помощью комплексных чисел много. Приводим одну из наиболее удобных.
Арифметические операции (сложение – код 0, умножение – код 1, деление –код 2) над парами комплексных чисел Z 1 = a1 + jb1 и Z 2 = а2 + jb2 выполняются в следующем порядке, ввод: a1, b1, a2, b2 – в регистр Х, код операции – в регистр Х, результат:
Z = а + jb: a – Р4 = PX. b – Р5 = PY.
Вводится программа последовательным нажатием клавиш <F><ПРГ> и далее набирается содержание программы по строчкам. После ввода программы нужно нажать клавиши <F> <АВТ> <B/O>
Контрольный пример:
Вычислить Z = ((5 – j3) * (3 + j2)) / ((5 + j3) * (2 – j4)) + (0,5 + 1). Вводим <5>, <С/П>, <->, <3>, <С/П>, <3>, <С/П>, <2>, <С/П> (на индикаторе высвечивается <0>), <1> (код умножения), <С/П>.
Содержание программы
| Х-П 4 | С/П | Х-П 5 | С/П | Х-П 2 | С/П | Х-П 3 | С/П | F Х≠0 | |
| – | F Х≠0 | П-Х 2 | F X2 | П-Х 3 | F X2 | + | |||
| Х-П 8 | П-Х 2 | П-Х 8 | + | Х-П 2 | П-Х 3 | /–/ | П-Х 8 | + | Х-П 3 |
| П-Х 3 | П-Х 5 | Х | Х-П 0 | П-Х 4 | П-Х 3 | Х | Х-П 1 | П-Х 2 | П-Х 5 |
| Х | П-Х 1 | + | Х-П 5 | П-Х 2 | П-Х 4 | Х | П-Х 0 | – | Х-П 4 |
| БП | П-Х 5 | П-Х 3 | + | Х-П 5 | П-Х 4 | П-Х 2 | + | Х-П 4 | |
| БП |
После получения результата вводим <5>, <С/П>, <3>, <С/П>, (на индикаторе высвечивается <0>). <2> (код деления), <С/П>. После получения результата вводим <2>, <С/П>, <–>, <4>, <С/П>, (на индикаторе высвечивается <0>), <2> (код деления), <С/П>. После получения результата вводим: <0,5>, <С/П>, <1>, <С/П>, (на индикаторе высвечивается <0>). <0> (код сложения), <С/П>:
Получаем: Z = PX + j PY = 1,1388235 + j1,4647059.
Каждое новое вычисление нужно начинать с нажатия клавиши <В/О>.
3.2 Характеристики и параметры цепей переменного тока в комплексной форме.
Так как теоретический материал по данной теме рассмотрен в учебниках, напомним только основные формулы.
Ток в комплексной форме:
I = I * ejy
где φ - начальная фаза, I - действующее значение тока.
Напряжение в комплексной форме:
U = U * ejy
Комплексное полное сопротивление:
Z = Z * ejφ = Z *(Cos φ 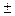 j Sin φ) = R
j Sin φ) = R 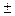 jX.
jX.
где знак "плюс" берётся для индуктивной нагрузки, а знак "минус" - для емкостной.
Комплексная полная проводимость:
Y = Y * ejφ = Y *(Cos φ 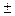 j Sin φ) = G
j Sin φ) = G 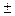 jB.
jB.
где знак "плюс" берётся при ёмкостной нагрузке, а знак "минус" – при индуктивной.
Комплексная полная мощность:
*
S = U * I = S * e 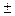 jφ = S *(Cos φ
jφ = S *(Cos φ 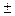 j Sin φ) = P
j Sin φ) = P 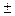 jQ.
jQ.
Где знак «плюс» берётся при индуктивной нагрузке, а знак «минус» – при ёмкостной.
Комплексную мощность приёмников можно определить и по более простой формуле: * *
S = U * I = I * Z * I
а так как произведение сопряжённых комплексов равно квадрату модуля, то есть *
I * I = I2,
мы получим формулу для определения комплексной мощности приёмников:
S = I2 * Z
3.3 Расчёт сложных цепей переменного тока символическим методом
3.3.1 Метод узловых и контурных уравнений
Составляем из заданных электроприёмников цепь с двумя узлами, как это показано на рисунке 3.3. Комплексная схема замещения такой цепи показана на рисунке 3.4.
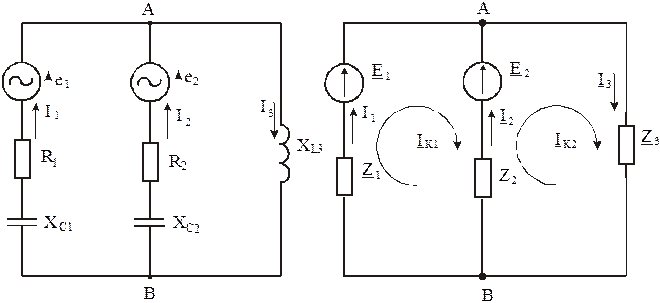 |
Рис. 3.3 Рис. 3.4
Сущность метода состоит в составлении системы уравнений по первому и второму законам Кирхгофа. Расчёт производим в следующем порядке.
По первому закону составляем (n – 1) независимых уравнений, где n – количество узлов в схеме. Выбираем узел А.. По второму закону нам остаётся составить два уравнения, так как число уравнений в системе должно быть равно количеству неизвестных токов, а их три. Направления токов в ветвях выбираются произвольно. Направления обхода контуров принимаем (условно) по часовой стрелке. Таким образом, система уравнений в комплексной форме включает в себя одно уравнение, составленное по первому закону Кирхгофа и два уравнения, составленные по второму закону:
 I 1 + I 2 – I 3 = 0;
I 1 + I 2 – I 3 = 0;
 I 1 Z 1 – I 2 Z 2 = E 1 – E 2;
I 1 Z 1 – I 2 Z 2 = E 1 – E 2;
I 2 Z 2 + I 3 Z 3 = E 2.
Подставляем заданные комплексы известных величин:
 I 1 + I 2 – I 3 = 0 (1);
I 1 + I 2 – I 3 = 0 (1);
 I 1 * (2 – j3) – I 2 * (14 – j12) = 100 – 65 (2);
I 1 * (2 – j3) – I 2 * (14 – j12) = 100 – 65 (2);
I 2 * (14 – j12) + I 3 * j18 = 65 (3).
Данную систему легче решить с помощью простых подстановок: из (2) определяем I 1, из (3) определяем I 3:
 I 1 + I 2 – I 3 = 0;
I 1 + I 2 – I 3 = 0;
 I 1 = (35+ I 2*(14-j12))/(2-j3) = 5,38 + j8,08+ I 2*(4,92+j1,38) (4);
I 1 = (35+ I 2*(14-j12))/(2-j3) = 5,38 + j8,08+ I 2*(4,92+j1,38) (4);
I 3 = (65- I 2*(14-j12))/j18 = –j3.61 – I 2*(–0,667 – j0,778) (5).
Подставляем (4) и (5) в (1) и получим:
5,38 + j8,08 + I 2*(4,92 + j1,38) + I 2 + j3,61 + I 2* (0,667 – j0,778) = 0;
5,38 + j8,08 + j3,61 = I 2 * (–4,92 – j1,38 – 1 + 0,667 + j0,0778);
5,38 +j11,68 = I 2 * (–5,253 – j0,602), отсюда
I 2 =(5.38+j11.68)/(-5.253-j0.602) = –1,26 – j2,08 = 2,438e - j121,21 A;
I 1 = 5,38 + j8,08 + (–1,26 – j2,08) * (4,92 + j1,38) = 2,05 – j3,89 = =4,4 * 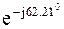 A.
A.
I 3 = –3,61 – (–1,26 – j2,08)*(–0,667 – j0,778) = 0,778 – j5,97 =
=6.02 * 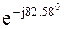 A.
A.
Составляем уравнение баланса мощностей в заданной электрической цепи. Определяем комплексные мощности источников:
S E1 = E 1* 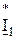 = 100 * (2,05 + j3,89) = 205 + j389 = 440 *
= 100 * (2,05 + j3,89) = 205 + j389 = 440 * 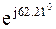 *В*A.;
*В*A.;
S E2 = E 2* 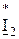 = 65 * (–1,26 + j2,08) = –81,9 + j135 = 158 *
= 65 * (–1,26 + j2,08) = –81,9 + j135 = 158 * 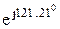 B*A.
B*A.
Определяем комплексные мощности приёмников электрической энергии:
S 1 = I12 * Z 1 = 4,42 * (2 – j3) = 38,7 – j58,1 B*A;
S 2 = I22 * Z 2 = 2,432 * (14 – j12) = 82,7 – j70,8 B*A;
S 3 = I32 * Z 3 = 6,022 * (j18) = j652 B*A.
Уравнение баланса комплексных мощностей!
S Е1 + S E2 = S 1 + S 2 + S 3;
205 + j389 – 81,9 + j135 = 38,7 – j58,1 + 82,7 – j70,8 + j652;

 123,1 + j524 = 121,4 + j523, или
123,1 + j524 = 121,4 + j523, или
538,3 * 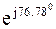 = 536,9 *
= 536,9 * 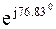 .
.
 Относительная погрешность в балансе полных мощностей составит:
Относительная погрешность в балансе полных мощностей составит:
YS = (538.3-536.9) * 100%/538.3 = 0,28% < 2%.
Угловая погрешность также незначительна.
Для построения векторной диаграммы задаёмся масштабами токов MI = 1 А/см и э.д.с. ME = 10 В/см.
Векторная диаграмма в комплексной плоскости построена на рисунке 3.5.
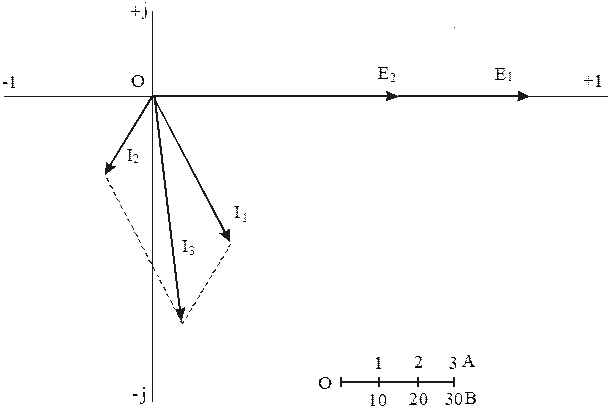
Рисунок 3.5
3.3.2 Метод контурных токов
Намечаем в независимых контурах заданной цепи, как показано на рисунке 3.4, контурные токи I K1 и I K2 – некоторые расчётные комплексные величины, которые одинаковы для всех ветвей выбранных контуров. Направления контурных токов принимаются произвольно. Для определения контурных токов составляем два уравнения по второму закону Кирхгофа:
 I K1 * (Z 1 + Z 2) – I K2 Z 2 = E 1 – E 2;
I K1 * (Z 1 + Z 2) – I K2 Z 2 = E 1 – E 2;
- I K1 * Z 2 + I K2 * (Z 2 + Z 3) = E 2.
Подставляем данные в систему:

 I K1 * (2 – j3 + 14 – j12) – I K2 * (14 – j12) = 100 – 65;
I K1 * (2 – j3 + 14 – j12) – I K2 * (14 – j12) = 100 – 65;
- I K1 * (14 – j12) + I K2 * (14 – j12 + j18) = 65.
 I K1 * (16 – j15) – I K2 * (14 – j12) = 35;
I K1 * (16 – j15) – I K2 * (14 – j12) = 35;
- I K1 * (14 – j12) + I K2 * (14 + j6) = 65.
Решаем систему с помощью определителей. Определитель системы:

 Δ =
Δ = 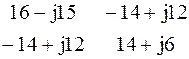 = (16 – j15) * (14 + j6) – (–14 + j12)2 = (314 – j114) – (52 – j336) = 262 + j222;
= (16 – j15) * (14 + j6) – (–14 + j12)2 = (314 – j114) – (52 – j336) = 262 + j222;
Частные определители:

 Δ 1 =
Δ 1 = 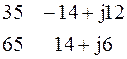 = 35 * (14 + j6) – 65*(–14 + j12) = (490 + j210) –
= 35 * (14 + j6) – 65*(–14 + j12) = (490 + j210) –
– (–910 + j780) = 1400 – j570;

 Δ 2 =
Δ 2 = 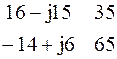 = (16 – j15) * 65 – (–14 + j12) * 35 = (1040 – j975) –
= (16 – j15) * 65 – (–14 + j12) * 35 = (1040 – j975) –
– (–490 + j420) = 1530 – j1395.
Определяем контурные токи:
I K1 = 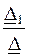 =
= 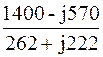 = 2,04 – j3,9 A;
= 2,04 – j3,9 A;
I K2 = 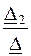 =
= 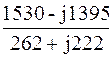 = 0,773 – j5,98 A.
= 0,773 – j5,98 A.
Действительные токи в ветвях цепи определяем как результат наложения контурных токов:
I 1 = I K1 = 2,04 – j3,9 = 4,4 * 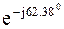 A;
A;
I2 = I K2 – I K1 = (0,773 – j5,98) – (2,04 – j3,9) = -1,27 – j2,08=2,44 * * 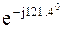 A;
A;
I 3 = I K2 = 0,773 – j5,98 = 6,03 * 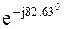 A.
A.
Уравнение баланса мощностей составлено при решении данного примера предыдущим методом.
3.3.3 Метод упрощения схем
Для того чтобы показать, как рассчитывать цепь методом упрощения схем, предположим, что в источнике с э.д.с. E 1 произошло короткое замыкание между зажимами, то есть E 1 = 0. Электрическая схема цепи и комплексная схема замещения представлены на рисунках 3.6 и 3.7.
Определяем эквивалентные сопротивления участков и всей цепи. Сопротивления Z 1 и Z 3 соединены параллельно, поэтому их эквивалентное сопротивление
Z 1 3 = 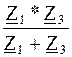 =
= 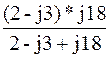 = 2,83 – j3,22 Ом
= 2,83 – j3,22 Ом
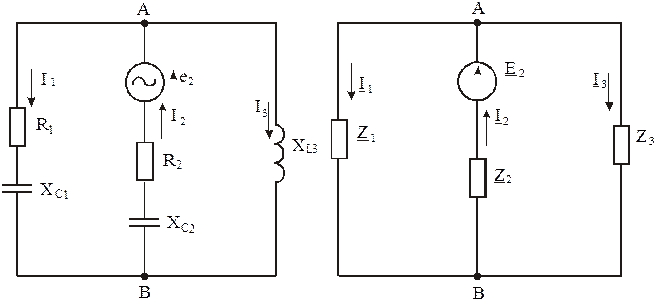
Рис. 3.6 Рис. 3.7
Сопротивления Z 1 3 и Z 2 соединены последовательно, поэтому эквивалентное сопротивление всей цепи
Z Э = Z 1 3 + Z 2 = 2,83 – j3,22 + 14 – j12 = 16,8 – j15,2 Ом.
Определяем ток в активной ветви:
I 2 = 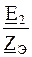 =
= 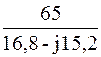 = 2,13 + j1,92 = 2,87 *
= 2,13 + j1,92 = 2,87 * 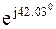 A.
A.
 Напряжение между узлами А и В:
Напряжение между узлами А и В:
U A B = I 2 * Z 1 3 = (2,13 + j1,92) * (2,83 – j3,22) = 12,2 – j1,41 B.
Токи в пассивных ветвях цепи:
I 1 = 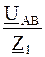 =
= 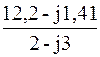 = 2,2 + j2,6 = 3,41 *
= 2,2 + j2,6 = 3,41 * 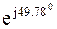 A.
A.
I 3 = 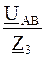 =
= 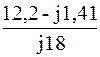 = –0,0783 – j0,678 = 0,682 *
= –0,0783 – j0,678 = 0,682 * 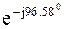 A.
A.
Уравнение баланса мощностей и векторная диаграмма выполняются аналогично примеру 3.3.1.
 2015-03-08
2015-03-08 3377
3377
