Идея симплекс метода состоит в последовательном продвижении по базисам опорных планов задачи, т.е. в последовательном улучшении планов задачи по определенному критерию, до тех пор, пока не будет найдено оптимальное решение.
Рассмотрим процесс подготовки исходных данных и алгоритм решения задачи ЛП табличным симплекс-методом.
Предварительный этап:
1. Привести математическую модель задачи к каноническому виду.
2. Определить начальное допустимое базисное решение задачи.
3. Ввести в исходную симплекс-таблицу параметр оценки 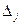 по формуле
по формуле
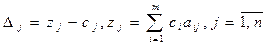
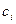 - весовые коэффициенты при базисных переменных.
- весовые коэффициенты при базисных переменных.
Алгоритм:
1. Заполняется исходная симплекс-таблица.
2. Если все 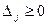 для всех
для всех 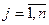 то данный план оптимален.
то данный план оптимален.
3. Если имеются 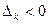 и в столбце
и в столбце 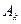 все элементы
все элементы 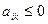 то функция не ограничена сверху на ОДР.
то функция не ограничена сверху на ОДР.
4. Если имеются 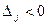 и в столбцах
и в столбцах 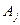 , соответствующих этим отрицательным оценкам, существует хотя бы один элемент
, соответствующих этим отрицательным оценкам, существует хотя бы один элемент 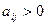 , то возможен переход к новому, лучшему плану, связанному с большим значением целевой функции.
, то возможен переход к новому, лучшему плану, связанному с большим значением целевой функции.
5. Вектор 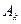 , который необходимо ввести в базис для улучшения плана, определяется по наименьшей отрицательной оценке
, который необходимо ввести в базис для улучшения плана, определяется по наименьшей отрицательной оценке 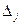 . Столбец, содержащий эту оценку, называется направляющим.
. Столбец, содержащий эту оценку, называется направляющим.
6. Вектор который нужно вывести из базиса, определяется по отношению
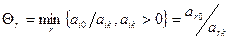 . Из базиса выводится вектор
. Из базиса выводится вектор 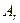 , на котором достигается минимум
, на котором достигается минимум 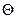 . Строка
. Строка 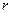 называется направляющей.
называется направляющей.
Элемент 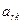 , который стоит на пересечении направляющей строки и направляющего столбца, называется направляющим.
, который стоит на пересечении направляющей строки и направляющего столбца, называется направляющим.
7. Заполняется таблица, соответствующая новому базисному решению.
Все элементы 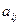 таблицы определяются по рекуррентному соотношению:
таблицы определяются по рекуррентному соотношению:
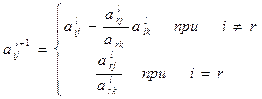
где l- номер итерации.
8. Процесс вычисления заканчивается, когда найдено оптимальное решение (пункт2) или когда функция будет неограниченной на ОДР (пункт 3).
Пример:
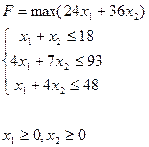
Приведем задачу к каноническому виду:
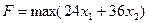
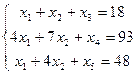
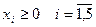
Построим начальную симплекс таблицу:
| Баз.перем. | Решение | А1 |  А2 А2 | А3 | А4 | А5 | 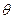 |
| Х3 | 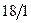 | ||||||
| Х4 | 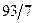 | ||||||
 Х5 Х5 | 4 | 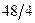 | |||||
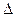 | -24 | -36 |
Строим новую симплекс-таблицу:
| Баз.перем. | Решение |  А1 А1 | А2 | А3 | А4 | А5 | 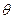 |
| Х3 | 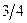 | 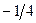 | 6* 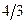 | ||||
 Х4 Х4 | 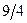 | 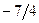 | 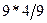 | ||||
| Х2 | 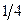 |  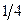 | 12*4 | ||||
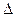 | -15 |
Строим новую симплекс-таблицу:
| Баз.перем. | Решение | А1 | А2 | А3 | А4 |  А5 А5 | 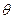 |
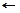 Х3 Х3 | 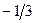 | 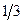 | |||||
| Х1 | 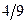 | 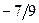 | - | ||||
| Х2 | 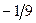 | 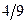 | 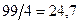 | ||||
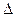 | 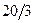 | 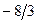 |
Строим новую симплекс-таблицу:
| Баз.перем. | Решение | А1 | А2 | А3 | А4 | А5 |
| Х5 | -1 | |||||
| Х1 | 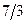 | 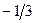 | ||||
| Х2 | 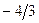 | 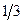 | ||||
 |
Получили оптимальный план:
Хопт= (11,7,0,0,9) Fопт=516
Вопрос для самоподготовки
1. Из каких основных двух моментов состоит симплекс?
2. Как определяется в симплекс методе тот факт, что задача ЛП решения не имеет?
3. В чем состоит идея симплекс метода?
4. Как определить вектор, который выводится из базиса?
5. Как прочитать решение задачи ЛП из последней симплекс таблицы?
ЛЕКЦИЯ 5.
 2015-03-20
2015-03-20 1069
1069
