Колебания и волны. Вопросы для программированного теоретического коллоквиума по физике, 2003 г

Вопросы для программированного теоретического коллоквиума по физике, 2003 г.

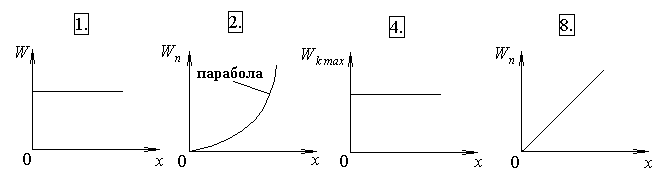
7.1. Ниже приведены графики зависимости полной W и потенциальной W _п энергии материальной точки от смещения х.

Какие графики могут соответствовать незатухающим гармоническим колебаниям материальной точки? Укажите сумму их номеров.

7.2. Материальная точка совершает незатухающие гармонические колебания вдоль оси 0 х. Для нее в произвольный момент времени t считаются следующие величины:

1. V_x – проекция скорости на ось 0 х (в момент времени t: х ¹ 0),

2. W_k – кинетическая энергия,

4. х – смещение (координата),

8. F – модуль результирующей силы, действующей на точку.

Получите выражение для угловой частоты w₀ колебаний точки через приведенные выше величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров.

7.3. Через какие из этих величин можно выразить потенциальную энергию W_n точки в момент времени t. Укажите суму их номеров.

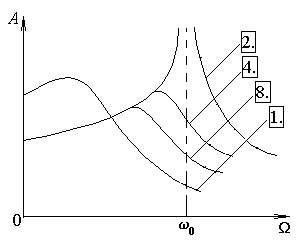7.4. На рисунке приведены графики зависимости амплитуды А вынужденных колебаний от частоты W вынуждающей силы для четырех систем с различными значениями коэффициента затухания колебаний b и одинаковой частотой w₀ собственных незатухающих колебаний.

В каком случае амплитуда F_m вынуждающей силы максимальна? Для какой системы коэффициент затухания b наименьший? Укажите сумму номеров соответствующих графиков.

7.5. На рисунке под номерами 4, 8 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 1, 2 – векторный диаграммы сложения гармонических колебаний одного направления и одинаковой частоты (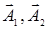 - векторы амплитуд складываемых колебаний, 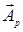- вектор амплитуды результирующего колебания).

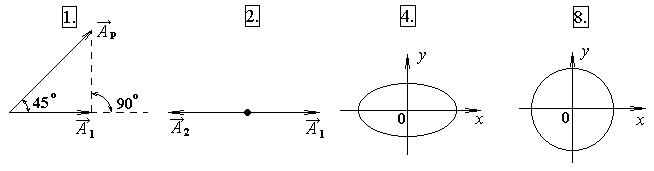
Для каких случаев разность фаз Dj складываемых колебаний равна p/2? Укажите сумму их номеров.

7.6. Для каких случаев амплитуды А ₁ и А ₂ складываемых колебаний одинаковы? Укажите сумму их номеров.

7.7. Период затухающих колебаний в колебательном контуре равен
Т = 2×10^-5 с. При каком логарифмическом декременте затухания æ амплитуда U_m напряжения на конденсаторе за время t = 10^-3 с меньше в е раз (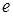 - основание натуральных логарифмов)?

7.8. В упругой среде распространяется плоская монохроматическая волна. Ниже стрелками указаны направления колебаний частиц среды.

В случае вектора скорости 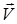волны может лежать в плоскости х 0 у, если волна продольная? Укажите сумму номеров соответствующих диаграмм.

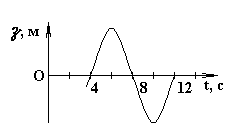
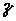7.9. В упругой среде распространяется плоская монохроматическая волна. В начальный момент времени t = 0 все частицы среды находились в покое. На рисунке приведен график зависимости от времени смещения частицы, отстоящей от источника колебаний на расстояние х = 2 м. Чему равны (в СИ) длина волны l?

7.10. Чему равна (в СИ) разность фаз Dj колебаний частиц среды, отстоящих от источника на расстояниях х ₁ = 2 м и х ₂ = 4 м?

7.11. Стоячая волна образовалась наложением бегущей и отраженной волн с длиной волны l = 14 м. На рисунке приведены графики смещения двух частиц среды в зависимости от времени. Чему равно минимальное расстояние D х между этими частицами?

7.12. В среде распространяется плоская электромагнитная волна. Известны следующие параметры волн и характеристики среды:

1. e - диэлектрическая проницаемость среды,

2. m - магнитная проницаемость среды,

4. Е_m – амплитуда напряженности электрического поля волны,

8. w - угловая частота волны.

Получите выражение для длины волны l в среде через приведенные выше величины и константы e₀, m₀, с. Укажите сумму номеров величин, вошедших в расчетную формулу.

7.13. Получите выражение для амплитудного значения S_m векторы Умова-Пойтинга через приведенные выше величины и константы e₀, m₀, с. Какие из обозначенных цифрами величин вошли в расчетную формулу? Укажите сумму их номеров.

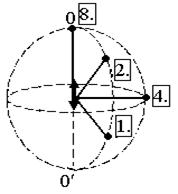7.14. На рисунке изображен электрический диполь, совершающий гармонические колебания вдоль оси 00^’. Цифрами 1, 2, 4, 8 обозначены различные направления в пространстве.

В каком направлении диполь не излучает электромагнитных волн?

Составители: М.Г. Валишев, Е.С. Левин, Ф.А. Сидоренко

ã ГОУ ВПО УГТУ-УПИ, Екатеринбург, 2003.