Общий вид уравнения с разделяющимися переменными имеет вид:
P1(x)Q1(y)dx + P2(x)Q2(y)dy =0.
Дифференциальное уравнение решается методом разделения переменных.
После почленного деления уравнения на Q1(y)P2(x) ¹ 0 получается дифференциальное уравнение с разделенными переменными, т.е. появляется возможность его интегрирования. После интегрирования получаем общее решение дифференциального уравнения:
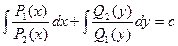 ,
,
где с – произвольная постоянная.
При проведении почленного деления дифференциального уравнения на Q1(y)P2(x) могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q1(y)P2(x) = 0 и установить решения дифференциального уравнения, которые не могут быть получены из общего уравнения. Они называются особыми решениями.
Уравнение y′ = f(ax + by + c), где а, b, с – действительные числа, сводится к уравнению с разделяющимися переменными после замены переменных ax + by + c = u. После дифференцирования a + by¢ = u¢, a + bf(u) = u¢, получим уравнение 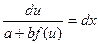 .
.
@ Задача 1. Найти общее решение дифференциального уравнения:
2yxdx – ( 1 + x ² )dy = 0.
Решение: После почленного деления уравнения на y(1 + x ² ) получаем: 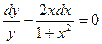 , которое легко интегрируется: ln/y/ – ln( 1 + x ² ) = ln/c/. Общее решение дифференциального уравнения имеет вид: y = с( 1 + x ² ).
, которое легко интегрируется: ln/y/ – ln( 1 + x ² ) = ln/c/. Общее решение дифференциального уравнения имеет вид: y = с( 1 + x ² ).
Уравнение y( 1 + x ² ) = 0 позволяет найти особое решение дифференциального уравнения: y = 0.
@ Задача 2. Найти частное решение дифференциального уравнения:
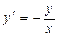 при y (1) = 1.
при y (1) = 1.
Решение: После почленного деления уравнения на y получаем: 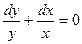 . Остается только интегрировать уравнение: ln/y/ + ln/x/ = ln/c/. Общее решение дифференциального уравнения имеет вид:
. Остается только интегрировать уравнение: ln/y/ + ln/x/ = ln/c/. Общее решение дифференциального уравнения имеет вид: 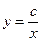 , а частное решение равно
, а частное решение равно 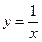 .
.
 2015-04-01
2015-04-01 1018
1018
