При изучении различных разделов техники, физики, экономики и других встречаются величины, которые вполне характеризуются заданием их численных значений. Такие величины называются скалярными (от слова "скаляр" – число). К скалярным величинам относятся, например, длина, площадь, объем, температура. Существуют, однако, и такие величины, для определения которых задание лишь численных значений недостаточно. Необходимо знать также их направление в пространстве. Такие величины называются векторными. К векторным величинам относятся, например, сила, скорость, ускорение и т.д. Векторные величины геометрически изображаются с помощью направленного отрезка – вектора.
1. Векторы, линейные операции над векторами
Вектор – это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление.
Вектор может обозначаться либо двумя большими буквами 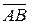 , где А – начало, а В – конец вектора; либо одной маленькой буквой
, где А – начало, а В – конец вектора; либо одной маленькой буквой 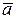 с чертой или стрелкой наверху.
с чертой или стрелкой наверху.
Вектор 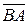 , у которого начало – в точке В, а конец – в точке А, называется противоположным вектору
, у которого начало – в точке В, а конец – в точке А, называется противоположным вектору 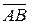 .
.
Длиной или модулем 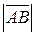 называется число, равное длине отрезка АВ.
называется число, равное длине отрезка АВ.
Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 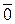 . У нулевого вектора начало и конец совпадают и он имеет произвольное направление (иногда говорят, что, наоборот, нулевой вектор направления не имеет).
. У нулевого вектора начало и конец совпадают и он имеет произвольное направление (иногда говорят, что, наоборот, нулевой вектор направления не имеет).
Вектор, длина которого равна 1, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора 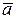 , называется ортом вектора
, называется ортом вектора 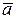 .
.
Выберем в пространстве какую-либо точку О, которую назовем началом координат, и проведем через нее три взаимно перпендикулярные оси. На каждой оси из точки О проведем единичные векторы.
Ось с выбранным началом отсчета и выбранной единицей длины называется координатной осью, а упорядоченная система трех взаимно перпендикулярных осей с общим началом отсчета и общей единицей длины называется прямоугольной декартовой системой координат в пространстве:
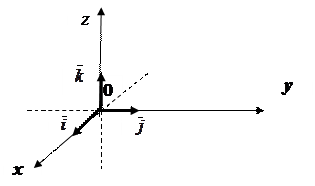
Координатные оси называются: О х – ось абсцисс; О у – ось ординат; О z – ось аппликат.
Единичные векторы, выходящие из начала координат и расположенные на координатных осях, называются координатными ортами.
Проведем в пространстве вектор 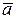 и опустим из начала и конца вектора перпендикуляры на оси координат, получим проекции этого вектора на соответствующие оси.
и опустим из начала и конца вектора перпендикуляры на оси координат, получим проекции этого вектора на соответствующие оси.
Координатами вектора называются его проекции на оси координат.
 |
Координаты вектора записываются, в отличие от координат точки, в фигурных скобках 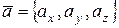
Вектор может быть записан через координатные орты, а именно
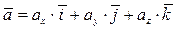
Формула называется разложением вектора 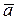 по координатным ортам.
по координатным ортам.
Длина или модуль вектора вычисляется по формуле
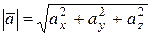
Пусть заданы координаты начальной и конечной точек вектора 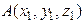 и
и 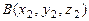 . Тогда вектор
. Тогда вектор 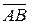 имеет следующие координаты:
имеет следующие координаты:
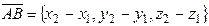
Векторы 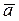 и
и 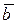 называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают 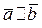 .
.
Коллинеарные векторы могут быть направлены одинаково или противоположно. Нулевой вектор считается коллинеарным любому вектору.
Два вектора 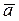 и
и 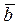 называются равными (
называются равными (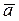 =
= 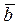 ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
), если они коллинеарны, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку пространства. Отсюда следует, что два вектора 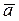 и
и 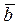 равны тогда и только тогда, когда выполняются равенства их одноименных координат, т.е.
равны тогда и только тогда, когда выполняются равенства их одноименных координат, т.е.
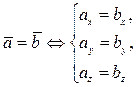
Над векторами можно проводить определенные операции, самыми простыми из которых являются линейные.
К линейным операциям над векторами относятся сложение и вычитание векторов, умножение вектора на число. Сами линейные операции над векторами сводятся к линейным операциям над координатами этих векторов.
Пусть даны два вектора 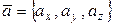 и
и 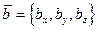 .
.
Суммой векторов 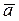 и
и 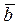 называется вектор, координаты которого равны сумме одноименных координат складываемых векторов, т.е.
называется вектор, координаты которого равны сумме одноименных координат складываемых векторов, т.е.
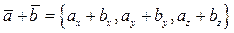 .
.
Произведением числа a на вектор 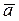 (или вектора на число) называется вектор, координаты которого являются произведением числа на координаты данного вектора, т.е.
(или вектора на число) называется вектор, координаты которого являются произведением числа на координаты данного вектора, т.е.
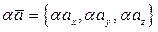 .
.
Нетрудно понять, что вектор a 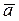 коллинеарен вектору
коллинеарен вектору 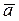 , имеет длину
, имеет длину 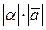 и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора 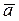 , при положительном a и противоположным направлению вектора
, при положительном a и противоположным направлению вектора 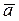 , при отрицательном a.
, при отрицательном a.
Разность двух векторов можно определить аналогично сумме, т.е. как вектор 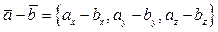 . Однако разность также можно представить как сумму вектора
. Однако разность также можно представить как сумму вектора 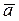 и вектора
и вектора 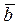 , умноженного на (-1).
, умноженного на (-1).
Выясним условие коллинеарности векторов, заданных своими координатами. Так как 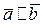 , то можно записать
, то можно записать 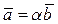 , где a - некоторое число. Таким образом, для координат этих векторов будет выполнено условие:
, где a - некоторое число. Таким образом, для координат этих векторов будет выполнено условие:
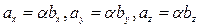
Отсюда 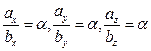 или
или 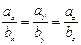 , т.е. справедливо следующее утверждение.
, т.е. справедливо следующее утверждение.
Теорема (необходимое и достаточное условия коллинеарности векторов). Координаты коллинеарных векторов пропорциональны, т.е.
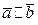
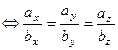 .
.
Кроме линейных операций существуют понятия различных произведений векторов: скалярное, векторное, смешанное, двойное векторное произведения векторов. Рассмотрим только скалярное произведение.
2. Скалярное произведение векторов и его свойства
Скалярным произведением двух векторов 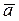 и
и 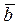 называется число, определяемое по формуле:
называется число, определяемое по формуле:
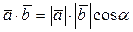 ,
,
где a - угол между векторами.
Скалярное произведение векторов обладает следующими свойствами:
1. 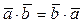 - переместительный закон.
- переместительный закон.
2. 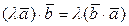 - сочетательный закон.
- сочетательный закон.
3. 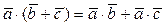 - распределительный закон.
- распределительный закон.
4. Скалярный квадрат вектора равен квадрату его длины: 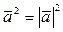 , в частности
, в частности 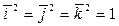 .
.
С помощью понятия скалярного произведения можно получить условие ортогональности векторов.
Теорема (необходимое и достаточное условие ортогональности векторов). Два ненулевых вектора 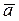 и
и 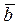 ортогональны в том и только в том случае, когда их скалярное произведение равно нулю, т.е.
ортогональны в том и только в том случае, когда их скалярное произведение равно нулю, т.е.
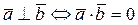 .
.
Из теоремы, в частности следует, что все скалярные произведения разных координатных орт равны нулю, т.е.
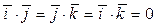 .
.
Если векторы заданы своими координатами, то скалярное произведение определяется как сумма произведений одноименных координат, т.е.
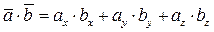
Формула легко получается, если векторы 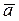 и
и 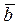 разложить по координатным ортам, т.е. представить в виде
разложить по координатным ортам, т.е. представить в виде 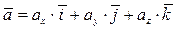 и
и 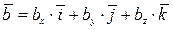 , а затем перемножить по правилу умножения многочленов. Окончательно получаем формулу, используя следующие вышеприведенные равенства:
, а затем перемножить по правилу умножения многочленов. Окончательно получаем формулу, используя следующие вышеприведенные равенства:
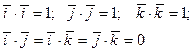
Пусть два вектора заданы своими координатами 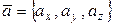 и
и 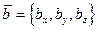 . Тогда угол между этими векторами можно определить по следующей формуле:
. Тогда угол между этими векторами можно определить по следующей формуле:
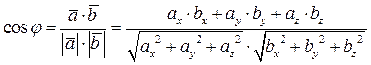 .
.
Отсюдаследует, что условие перпендикулярности ненулевых векторов выглядит следующим образом:
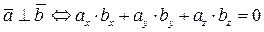 .
.
 2015-04-23
2015-04-23 882
882








