Поверхности второго порядка

Классификация кривых второго порядка

Рассмотрим общее уравнение второго порядка (11.5):

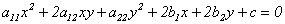
и выясним, какие геометрические образы на плоскости могут задаваться этим уравнением.

1. Если собственные числа матрицы А λ ₁ и λ ₂ одного знака, уравнение (11.5) называется уравнением эллиптического типа. Его можно привести к виду (11.7): 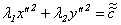, которое, в свою очередь, преобразуется в следующую форму:

а) если 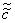имеет тот же знак, что и λ _1,2, при делении на  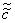получаем

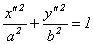- каноническое уравнение эллипса.

б) если 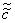= 0, уравнение  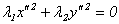имеет единственное решение: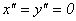, определяющее точку на плоскости.

в) если знак 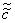 противоположен знаку λ _1,2, уравнение после деления на  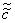примет вид:

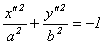. Множество его решений пусто (иногда это пустое множество называют мнимым эллипсом).

2. Если собственные числа матрицы А λ ₁ и λ ₂ разных знаков, уравнение (11.5) называется уравнением гиперболического типа.

а) при 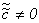 оно сводится к одному из двух видов:

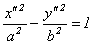или 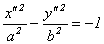, в зависимости от знака 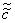. Оба этих уравнения определяют гиперболу.

б) При 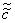= 0 получаем уравнение 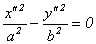, эквивалентное двум линейным уравнениям: 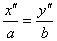и 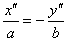, задающим пару пересекающихся прямых.

3. Если одно из собственных чисел равно 0, уравнение (11.5) называется уравнением параболического типа, и его можно привести к одному из следующих видов:

а) к уравнению (11.8): 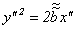, определяющему параболу;

б) к уравнению 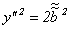, или 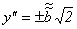, задающему пару параллельных прямых;

в) к уравнению 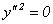, определяющему одну прямую (или пару совпадающих прямых);

г) к уравнению 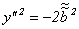, не имеющему решений и, следовательно, не определяющему никакого геометрического образа.

Определение 12.1. Поверхностью второго порядка называется множество точек трехмерного пространства, декартовы координаты которых удовлетворяют уравнению вида:

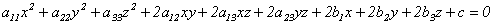- (12.1)

уравнению второй степени от трех неизвестных, называемому общим уравнением поверхности второго порядка.

Если найти собственные числа и нормированные собственные векторы матрицы квадратичной формы 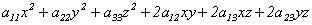и перейти к системе координат, определяемой базисом из ортонормированных собственных векторов, уравнение (12.1) можно привести к одному из следующих видов:

1. Если λ ₁, λ ₂, λ ₃ – одного знака, уравнение (12.1) есть уравнение эллиптического типа и приводится к канонической форме:

а) 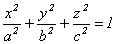- (12.2)

каноническое уравнение эллипсоида.

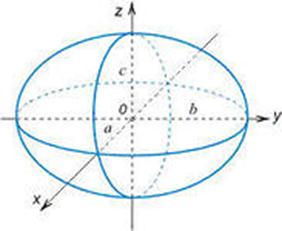
Замечание, Если два собственных числа совпадают, эллипсоид называется эллипсоидом вращения и представляет собой поверхность, полученную в результате вращения эллипса вокруг одной из его осей. Если все собственные числа равны, уравнение (12.2) становится уравнением сферы.

б) 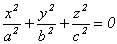- (12.3)

уравнение задает точку в пространстве;

в) 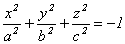- (12.4)

пустое множество.

2. Если собственные числа разных знаков, уравнение (12.1) приводится к каноническому виду:

а) 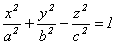- каноническое уравнение однополостного гиперболоида, (12.5)

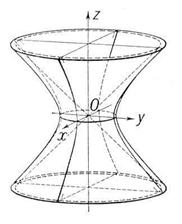
б) 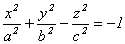- (12.6)

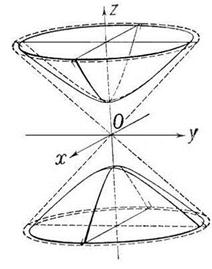
- каноническое уравнение двуполостного гиперболоида,

в) 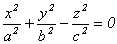- (12.7)

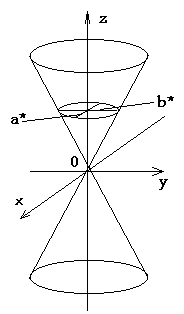
уравнение конуса второго порядка.

3. Одно из собственных чисел равно 0. При этом с помощью преобразований координат можно получить следующие формы уравнения (12.1):

а) 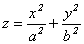- (12.8)

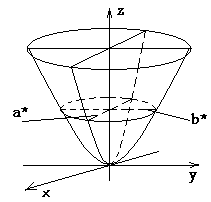
каноническое уравнение эллиптического параболоида,

б) 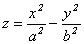- (12.9)

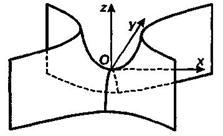
каноническое уравнение гиперболического параболоида и уравнения цилиндрических поверхностей:

в) 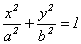 - эллиптический цилиндр, (12.10)

г) 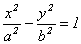 - гиперболический цилиндр. (12.11)

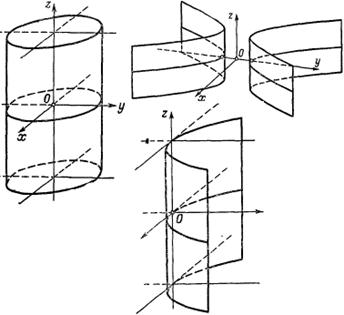
Наконец, уравнение может определять пару плоскостей:

д) 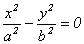. (12.12)

4. Если два собственных числа равны 0, уравнение (12.1) приводится к одному из следующих видов:

а) 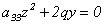 - параболический цилиндр, (12.13)

б) 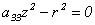 - пара параллельных плоскостей, (12.14)

в) 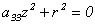 - пустое множество.