Определение 5.6. Случайная величина Х называется непрерывной, если ее функцию распределения 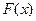 можно представить в виде
можно представить в виде
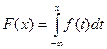 . . | (5.1) |
Функцию 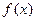 называют плотностью распределения (вероятностей) случайной величины Х.
называют плотностью распределения (вероятностей) случайной величины Х.
Предполагается, что несобственный интеграл в формуле (5.1) сходится.
Свойства плотности распределения 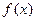 .
.
1. 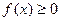 для всех
для всех 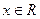 – условие неотрицательности плотности.
– условие неотрицательности плотности.
2. 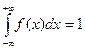 – условие нормировки.
– условие нормировки.
3. 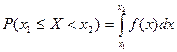 .
.
4. Если 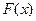 – дифференцируемая функция, то
– дифференцируемая функция, то 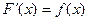 .
.
Рассмотрим наиболее важные распределения непрерывных случайных величин.
1. Равномерное распределение. Говорят, что непрерывная случайная величина 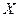 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 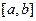 , если ее плотность распределения
, если ее плотность распределения
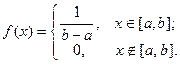
Функция распределения в этом случае определяется выражением:
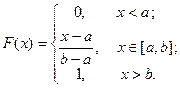
Заметим, что равномерное распределение реализует схему геометрической вероятности при бросании точки на отрезок  .
.
2. Показательное распределение. Говорят, что непрерывная случайная величина 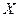 распределена по показательному (экспоненциальному) закону, если она имеет плотность распределения
распределена по показательному (экспоненциальному) закону, если она имеет плотность распределения
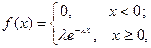


где 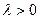 – параметра показательного распределения.
– параметра показательного распределения.
Функция распределения показательного распределения имеет вид
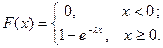
3. Нормальное распределение. Случайная величина 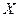 имеет нормальное (гауссовское) распределение с параметрами
имеет нормальное (гауссовское) распределение с параметрами 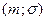 , если ее плотность распределения имеет вид
, если ее плотность распределения имеет вид
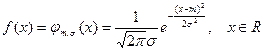 .
.
При 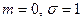 – это так называемое стандартное нормальное распределение, плотностью которого является встречавшаяся ранее функция Гаусса
– это так называемое стандартное нормальное распределение, плотностью которого является встречавшаяся ранее функция Гаусса
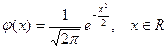 .
.
Функция распределения нормального распределения случайной величины является интегралом, не выражаемым через элементарные функции:
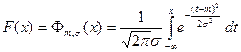 .
.
При произвольных значениях параметров 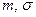 для функции нормального распределения справедлива формула
для функции нормального распределения справедлива формула
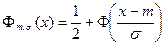 ,
,
где 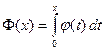 – интеграл Лапласа (таблица 3 приложения). При этом вероятность того, что случайная величина Х примет значение, принадлежащее интервалу
– интеграл Лапласа (таблица 3 приложения). При этом вероятность того, что случайная величина Х примет значение, принадлежащее интервалу 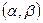 ,
,
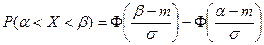 . . | (5.2) |
Пример 5.3. Задана плотность распределения непрерывной случайной Х:
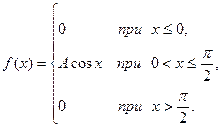
Найти постоянный параметр А, функцию распределения 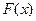 . Вычислить вероятность попадания случайной величины Х в интервал
. Вычислить вероятность попадания случайной величины Х в интервал 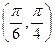 .
.
Решение. 1. Для нахождения постоянного параметра А воспользуемся условием нормировки плотности распределения: 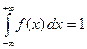 . Тогда для заданной функции получаем:
. Тогда для заданной функции получаем:
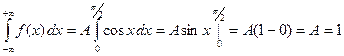 ,
,
отсюда 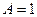 и плотность распределения примет вид:
и плотность распределения примет вид:
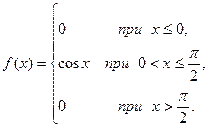
2. Найдем функцию распределения 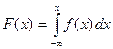 .
.
Если 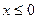 , то
, то 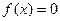 , следовательно,
, следовательно, 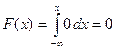 .
.
Если 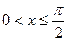 , то
, то 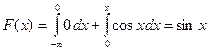 .
.
Если 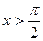 , то
, то 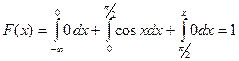 .
.
Таким образом, искомая функция распределения 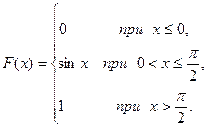
3. 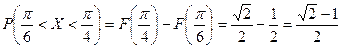 .
.
Пример 5.4. Случайная величина Х распределена по нормальному закону с параметрами 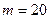 ,
, 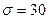 . Найти вероятность попадания случайной величины Х в интервал
. Найти вероятность попадания случайной величины Х в интервал 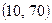 .
.
Решение. Воспользуемся формулой (5.2), тогда
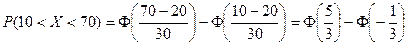 .
.
По таблице 3 приложения находим:
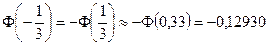 ,
, 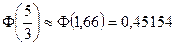 ,
,
откуда окончательно получаем
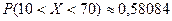 .
.
 2015-06-10
2015-06-10 1879
1879
