МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра высшей математики
УТВЕРЖДАЮ
Проректор по учебной работе
___________ О.Г.Локтионова
«____»___________2014г.
Векторная алгебра.
Индивидуальные задания и методические указания
по выполнению модуля
Курск 2014
УДК 514.12
Составитель А.В.Бойков
Рецензент
Кандидат физико-математических наук, доцент
кафедры высшей математики Дмитриев В.И.
Векторная алгебра. Аналитическая геометрия: индивидуальные задания и методические указания по выполнению модуля / Юго-Зап. гос. ун-т; сост.: А.В.Бойков. Курск, 2014. 30 с. табл. 3. Ил.: 2, Библиогр.: с.30.
Методические указания отражают требования образовательных стандартов 3-го поколения подготовки бакалавров и специалистов по техническим специальностям. Работа содержит теоретические индивидуальные упражнения, практические индивидуальные задания, контрольные вопросы, указания к использованию ЭВМ, рекомендуемую литературу по темам “Векторная алгебра” и “Аналитическая геометрия”.
Предназначены для студентов технических специальностей
Текст печатается в авторской редакции
Подписано в печать _______. Формат 60х84 1/16.
Усл. печ. л.1,75. Уч.-изд. л.1,58. Тираж 100 экз. Заказ. Бесплатно.
Юго-Западный государственный университет.
305040, Курск, ул. 50 лет Октября, 94.
СОДЕРЖАНИЕ
Введение…………………………………………………….4
1. Индивидуальные задания……………………………….5
1.1. Теоретические упражнения……………………...…5
1.2. Практические задания………………………………8
1.2.1. Задание 1………………………………………..8
1.2.2. Задание 2………………………………………..9
1.2.3. Задание 3………………………………………10
1.2.4. Задание 4………………………………………10
1.2.5. Задание 5………………………………………11
1.2.6. Задание 6………………………………………11
1.2.7. Задание 7………………………………………11
1.2.8. Задание 8………………………………………11
1.2.9. Задание 9………………………………………11
1.2.10. Задание 10……………………………………..15
1.2.11. Задание 11……………………………………..23
1.2.12. Задание 12………………………………….….24
2. Использование ЭВМ…………………………………...24
3. Контрольные вопросы…………………………………28
Список рекомендуемой литературы…………………….30
ВВЕДЕНИЕ
Цель преподавания математики в вузе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.
Важным фактором усвоения математики и овладения ее методами является самостоятельная работа студента. В Юго-Западном государственном университете самостоятельная работа студентов организуется на основе положения о бально-рейтинговой системе оценки качества освоения основных образовательных программ и имеет модульную структуру. Опыт нашего и других вузов показывает, что эта система активизирует самостоятельную работу студентов и способствует более глубокому изучению курса математики.
Предлагаемые методические указания являются пособием к одному из модулей этой системы. Методические указания посвящены разделам “Векторная алгебра” и “Аналитическая геометрия” (до тем кривые и поверхности второго порядка) и содержат индивидуальные задания (теоретическое упражнение и практические задания), контрольные вопросы, рекомендуемую литературу, указания к использованию ЭВМ (Маthcad) при выполнении заданий модуля. Указания по выполнению заданий модуля приводятся в пособии [7].
Предусмотрены три уровня сложности заданий модуля. Студенту предлагается выполнить одно теоретическое упражнение и некоторое количество практических заданий, в зависимости от выбранного им (или преподавателем) уровня сложности (или направления подготовки):
первый уровень - №№ 3-5, 8, 9(а,б), 11(а,б);
второй уровень - №№ 1-9, 11(а-е,и-л);
третий уровень - №№ 1-12.
Выбор индивидуального задания к модулю-2 осуществляется по номеру варианта студента n. При этом используются параметр Рк − остаток от деления номера варианта n на число к, и выражение [n / k] − целая часть от деления n на k. Например, если n = 7, то Р2=1, Р3=1, Р4=3, Р5=2, Р6=1, Р7=0, Р8=7, Р9=7 и т.д. Если n = 7 и к = 4, то [n/k] = [7/4] = 1.
1.1. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
Выполнить теоретическое упражнение номер m, где 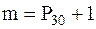 .
.
1. Сформулировать и доказать свойства проекции вектора на ось.
2. Записать и доказать соотношения между координатами вектора
и координатами точек “начала” и “конца” вектора.
3. Сформулировать и доказать необходимое и достаточное условие коллинеарности векторов.
4. Записать и доказать формулы, выражающие координаты точки,
делящей отрезок в заданном отношении, через координаты концов этого отрезка.
5. Записать и доказать формулы для длины и направляющих косинусов вектора, выражающие эти величины через декартовы ко-
ординаты вектора.
6. Доказать свойства скалярного произведения векторов.
7. Записать и доказать формулу, выражающую скалярное произведение векторов через их декартовы координаты.
8. Сформулировать и доказать необходимое и достаточное условие ортогональности векторов.
9. Записать и доказать формулы для косинуса угла между двумя векторами в пространствах V2 и V3.
10. Доказать свойство [ 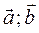 ] = − [
] = − [ 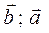 ] векторного произведения
] векторного произведения
векторов.
11. Используя свойства векторного произведения, доказать фор-
мулу, выражающую векторное произведение векторов через
их декартовы координаты.
12. Записать и доказать формулы для вычисления площади параллелограмма и треугольника с помощью векторного произведения векторов.
13. Записать и доказать формулу, выражающую смешанное про-
изведение векторов через их декартовы координаты.
14. Доказать свойства смешанного произведения векторов.
15. Записать и доказать формулы для вычисления объема параллелепипеда и треугольной пирамиды с помощью смешанного
произведения векторов.
16. Сформулировать и доказать необходимое и достаточное условие компланарности векторов пространства V3.
17. Доказать, что любая прямая на плоскости имеет уравнение
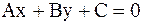 , где
, где 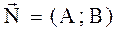 нормальный вектор этой прямой.
нормальный вектор этой прямой.
18. Вывести уравнение прямой на плоскости, проходящей через
точку М0(х0;у0) с угловым коэффициентом k.
19. Доказать, что любая прямая на плоскости имеет параметрические уравнения
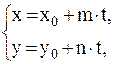
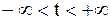 ,
,
где 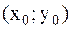 − произвольная точка прямой, а вектор
− произвольная точка прямой, а вектор 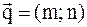 –
–
направляющий вектор этой прямой. Записать каноническое
уравнение прямой.
20. Доказать, что любая прямая в пространстве имеет параметри-
ческие уравнения
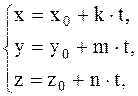
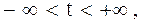
где (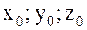 ), − произвольная точка прямой, а вектор
), − произвольная точка прямой, а вектор
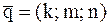 − направляющий вектор этой прямой. Записать
− направляющий вектор этой прямой. Записать
каноническое уравнение прямой.
21. Вывести формулу для косинуса угла между двумя прямыми на плоскости, заданными общими уравнениями. Доказать условия параллельности и перпендикулярности прямых.
22. Вывести формулу для тангенса угла между двумя прямыми на плоскости, заданными уравнениями с угловым коэффициентом. Сформулировать и доказать условия параллельности и перпендикулярности прямых.
23. Вывести формулу для косинуса угла между двумя прямыми на
плоскости, заданными каноническими (параметрическими)
уравнениями. Сформулировать и доказать условия параллель-
ности и перпендикулярности прямых.
24. Записать и доказать формулы для расстояния от точки до пря-
мой на плоскости и от точки до плоскости в пространстве.
25. Записать и доказать формулу для расстояния от точки до пря-
мой в пространстве.
26. Доказать, что любая плоскость в пространстве имеет уравнение 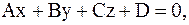 где
где 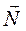 = (A;B;C) нормальный вектор этой плоскости.
= (A;B;C) нормальный вектор этой плоскости.
27. Вывести уравнение плоскости проходящей через три заданные
точки, не лежащие на одной прямой.
28. Вывести формулу для косинуса угла между двумя плоскостя-
ми. Сформулировать и доказать условия параллельности и
перпендикулярности плоскостей.
29. Вывести формулу для косинуса угла между двумя прямыми в
пространстве, заданными каноническими (параметрическими)
уравнениями. Сформулировать и доказать условия параллель-
ности и перпендикулярности прямых.
30. Вывести формулу для синуса угла между прямой и плос-
костью. Сформулировать и доказать условия параллельности
и перпендикулярности прямой и плоскости.
1.2. ПРАКТИЧЕСКИЕ ЗАДАНИЯ

1.2.1. ЗАДАНИЕ 1 
Решить задачу номер m из табл.1.1, где m = Р4 +1.
Таблица 1.1
Индивидуальные условия к заданию 1
| № задачи m | Условие задачи | Угол α | ||||
А О 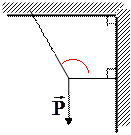 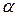 С В С В | К двум тросам подве- шен груз 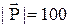 кГ Определить силы (в кГ), возникающие в тросах, если угол АСВ равен α, угол ОВС равен 90˚ кГ Определить силы (в кГ), возникающие в тросах, если угол АСВ равен α, угол ОВС равен 90˚ | 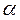 =90˚+2˚·([n/4]+1) =90˚+2˚·([n/4]+1) | ||||
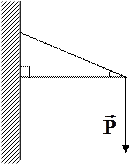 А А 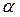 С В С В | Груз весом | 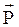 |=100кГ поддерживается двумя стержнями АВ и СВ. Определить силы (в кГ), возникающие в стержнях, если угол АСВ равен 90˚, угол АВС равен α |=100кГ поддерживается двумя стержнями АВ и СВ. Определить силы (в кГ), возникающие в стержнях, если угол АСВ равен 90˚, угол АВС равен α | α = 3°·([n/4] + 1) | ||||
 |
А В
С | К двум тросам АС и ВС, одинаковой длины, подвешен груз весом 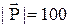 кГ. Определить силы (в кГ), возникающие в тросах, если угол АСВ равен α кГ. Определить силы (в кГ), возникающие в тросах, если угол АСВ равен α | α = 6˚·([n/4] + 1) |
Продолжение табл. 1.1
 С В С В  А А | Груз весом 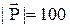 кГ поддерживается двумя стержнями АС и ВС. Определить силы (в кГ), возникающие в стержнях, если угол ВАС равен α, и угол АВС равен 120˚ кГ поддерживается двумя стержнями АС и ВС. Определить силы (в кГ), возникающие в стержнях, если угол ВАС равен α, и угол АВС равен 120˚ | α = 2˚·([n/4] + 1) | |


 1.2.2. ЗАДАНИЕ 2
1.2.2. ЗАДАНИЕ 2
Решить задачу номер m из табл.1.2, где m = Р5 + 1
Таблица 1.2
Индивидуальные условия к заданию 2
| № задачи m | Условие задачи |
Точка О − точка пересечения медиан треугольника АВС. Найти координаты точки В, если 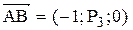 , , 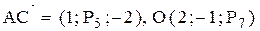 | |
Точка О − точка пересечения медиан треугольника АВС. Найти координаты точки О, если  А(Р3;−1;−2), С(−3;Р5;1), А(Р3;−1;−2), С(−3;Р5;1), 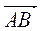 = (4;0;Р7) = (4;0;Р7) |
Продолжение табл. 1.2
В параллелограмме АВСD точка К − середина стороны СD. Найти координаты точки А, если 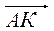 = (1;−5;Р3), = (1;−5;Р3), 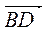 = (−2;Р7;−3), В(Р5;0;7) = (−2;Р7;−3), В(Р5;0;7) | |
| В параллелограмме АВСD точка О − точка пересечения диагоналей. Найти координаты точки К, − середины стороны АD, если В(Р3; Р5; Р7), С(−2;1;−3), О(4;0;−1) | |
В трапеции АВСD стороны АВ и СD - основания, Точка N(Р7;Р3;P5) − середина стороны ВС. Найти координаты точки А, если 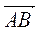 = (8;12;−4), = (8;12;−4), 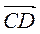 = (−2;−3;1), = (−2;−3;1), 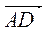 = (5;0;7) = (5;0;7) |
1.2.3. ЗАДАНИЕ 3
Даны три силы: 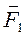 = P2·
= P2· 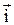 + 2·
+ 2· 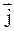 − 7·
− 7· 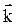 ,
, 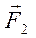 = 3·
= 3· 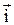 + P3·
+ P3· 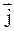 + 4·
+ 4· 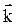 и
и 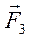 = −2·
= −2· 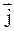 + Р5·
+ Р5· 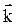 . Найти равнодействующую
. Найти равнодействующую 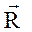 сил
сил 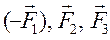 и работу, которую она производит, когда точка её приложения, двигаясь прямолинейно, перемещается из положения М0 (0;1; P7 ) в положение М (Р6; 0; 1).
и работу, которую она производит, когда точка её приложения, двигаясь прямолинейно, перемещается из положения М0 (0;1; P7 ) в положение М (Р6; 0; 1).
1.2.4. ЗАДАНИЕ 4
Сила 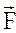 = (P3 ; P5; −2) приложена к точке С (Р4 ; −1; P7). Определить величину (модуль) и направление (направляющие косинусы) момента этой силы относительно начала координат.
= (P3 ; P5; −2) приложена к точке С (Р4 ; −1; P7). Определить величину (модуль) и направление (направляющие косинусы) момента этой силы относительно начала координат.
1.2.5. ЗАДАНИЕ 5
Найти ненулевой вектор ортогональный векторам
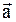 = (1 − Р4; P5 + 1; −3) и
= (1 − Р4; P5 + 1; −3) и 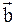 = (P3 – 1; 1; 4 – P7). Сделайте проверку.
= (P3 – 1; 1; 4 – P7). Сделайте проверку.
1.2.6. ЗАДАНИЕ 6
Даны точки: А(−1;−P3; 2), B(P5; 2; 0) и C(P5·(P3 +2); P32 + 3×Р3 +4; Р8 − 2·(Р3+1)). Образуют ли эти точки треугольник?
Если да, то чему равна его площадь?
Если нет, то запишите формулу для нахождения площади треугольника средствами векторной алгебры.
1.2.7. ЗАДАНИЕ 7
Даны точки: A(1; −P2; -1), B(1−P3 ; 0; 1), C(−1; 1; P5−2), D(P2 ; P4 ; P8). Образуют ли эти точки пирамиду?
Если да, то чему равен объём пирамиды?
Если нет, то запишите формулу для нахождения объёма пирамиды средствами векторной алгебры.
1.2.8. ЗАДАНИЕ 8
Даны точки А(−1–Р7 ; P5 −2) и В(Р5 – 2; P5 + 4). Найти:
а) точку С(х1 ; y1) − середину отрезка АВ;
б) точку D(x2 ; y2), которая делит отрезок АВ в отношении
(Р9 + 1): (9 – P9).
1.2.9. ЗАДАНИЕ 9
На плоскости даны точки А(х1; y1), B(x2; y2), C(x3; y3).
Координаты точек взять в табл. 1.3.
Сделайте чертёж треугольника АВС и найдите:
а) длину и уравнение стороны ВС (записать общее уравнение, каноническое, параметрические и с угловым коэффициентом);
б) косинус угла А и угол А (в градусах);
в) уравнение прямой, проходящей через точку А параллельно стороне ВС;
г) высоту, проведенную к стороне ВС, и её уравнение;
д) уравнение медианы, проведенной к стороне ВС;
е) уравнение биссектрисы угла А.
Таблица 1.3
Координаты точек А, В, С к заданию 9
| n | x1 | y1 | x2 | y2 | x3 | y3 |
| −1 | −1 | −7 | −1 | |||
| −1 | −1 | −1 | ||||
| −7 | −2 | −2 | ||||
| −1 | −1 | −5 | −1 | |||
| −5 | −2 | −5 | ||||
| −1 | −1 | −2 | −2 | |||
| −6 | −4 | |||||
| −5 | −6 | |||||
| −2 | −2 | |||||
| −3 | −11 | −3 | ||||
| −7 | −7 | |||||
| −4 | −3 | −3 | ||||
| −1 | −7 | −1 | ||||
| −1 | −3 | |||||
| −9 | −11 | |||||
| −5 | −14 | |||||
| −3 | −1 | −9 | ||||
| −5 | −3 | |||||
| −9 | −9 | −5 | −5 | |||
| −7 | −3 | −7 | ||||
| −6 | −2 | −2 | ||||
| −2 | −4 | |||||
| −1 | −1 | −8 | −1 | |||
| −7 | −7 | −4 |
Продолжение табл. 1.3
| −6 | −14 | −6 | −8 | |||
| −7 | −2 | −2 | ||||
| −5 | −1 | −1 | −1 | |||
| −5 | −4 | |||||
| −3 | −1 | −3 | ||||
| −1 | −6 | |||||
| −9 | ||||||
| −7 | −3 | −7 | ||||
| −9 | −3 | −1 | ||||
| −3 | −8 | −8 | −3 | |||
| −7 | −7 | |||||
| −4 | −4 | −3 | ||||
| −1 | −7 | −1 | ||||
| −8 | −1 | −1 | −1 | |||
| −4 | −7 | −7 | ||||
| −3 | −1 | −1 | ||||
| −7 | −1 | −1 | −1 | |||
| −5 | −3 | |||||
| −9 | −1 | −1 | ||||
| −7 | −3 | −7 | ||||
| −2 | −2 | −6 | ||||
| −5 | −6 | |||||
| −4 | −6 | |||||
| −3 | −3 | −3 | ||||
| −2 | −5 | |||||
| −6 | −8 | −6 | −14 | |||
| −5 | −2 | |||||
| −1 | −2 | −1 | ||||
| −5 | −5 | −2 | ||||
| −3 | −6 | −1 | −3 | |||
| −11 | −11 | −8 | ||||
| −9 | ||||||
| −11 | −9 | |||||
| −3 | −2 | −2 | ||||
| −3 | −3 | −11 | ||||
| −7 | −7 | |||||
| −1 | −3 | −3 | ||||
| −3 | −7 | −7 | ||||
| −4 | −6 | −6 | −1 |
Продолжение табл. 1.3
| −1 | −3 | |||||
| −1 | −7 | −1 | −1 | |||
| −2 | −6 | −2 | ||||
| −2 | −10 | −18 | ||||
| −3 | −5 | |||||
| −3 | −3 | −4 | ||||
| −7 | −5 | −5 | ||||
| −5 | −6 | |||||
| −4 | −6 | |||||
| −8 | −6 | −1 | −8 | |||
| −3 | −3 | −6 | −1 | |||
| −11 | −9 | |||||
| −14 | −6 | −8 | −6 | |||
| −1 | −3 | −3 | ||||
| −6 | −6 | −8 | ||||
| −9 | −3 | −1 | ||||
| −9 | ||||||
| −7 | −7 | −3 | ||||
| −1 | −3 | −3 | −6 | |||
| −7 | −1 | |||||
| −3 | −7 | −7 | ||||
| −7 | −1 | −1 | ||||
| −5 | −2 | |||||
| −3 | −5 | −3 | −11 | |||
| −3 | −3 | −11 | ||||
| −5 | −1 | −1 | −1 | |||
| −4 | −4 | |||||
| −5 | −5 | −2 | ||||
| −8 | −1 | −1 | −1 | |||
| −5 | −1 | |||||
| −7 | −4 | −7 | ||||
| −2 | −7 | −2 | ||||
| −13 | −1 | −1 | ||||
| −3 | −4 | −3 | ||||
| −2 | ||||||
| 100 100 | −1 | −3 |
1.2.10. ЗАДАНИЕ 10
Решить задачу номер n.
1. На прямой 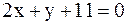 найти точку, равноудалённую от двух данных точек A(1;1), B(3,0).
найти точку, равноудалённую от двух данных точек A(1;1), B(3,0).
2. Найти координаты точки, симметричной точке (2,−4) относительно прямой 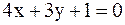 .
.
3. Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон 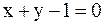 и
и 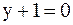 , если известно, что диагонали параллелограмма пересекаются в точке P(−1;0).
, если известно, что диагонали параллелограмма пересекаются в точке P(−1;0).
4. Составить уравнение прямой, проходящей через точку A(2;6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв.ед.
5. Составить уравнение прямой, проходящей через точку A(−1,2) так, что середина её отрезка, заключённого между параллельными прямыми 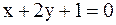 и
и 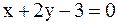 лежит на прямой
лежит на прямой 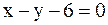 .
.
6. Даны уравнения двух сторон треугольника 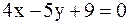 и
и 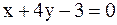 . Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке (3;1).
. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке (3;1).
7. Вычислить координаты вершин ромба, если известны уравнения двух его сторон 2x − y + 4 = 0 и 2x − y + 10 = 0 и уравнение одной из его диагоналей x + y + 2 = 0.
8. Составить уравнения сторон треугольника, если точки A(−5;5), B(3;1) - две его вершины, а D(2;5) − точка пересечения его высот.
9. Дано уравнение одной из сторон квадрата 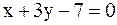 и точка пересечения его диагоналей P(0;−1). Найти уравнения трех остальных сторон этого квадрата.
и точка пересечения его диагоналей P(0;−1). Найти уравнения трех остальных сторон этого квадрата.
10. Даны уравнения одной из сторон ромба x −3y + 10 = 0 и одной из его диагоналей x + 4y − 4 =0. Диагонали ромба пересекаются в точке P(0;1). Найти уравнения трех остальных сторон ромба.
11. Уравнения двух сторон параллелограмма x + 2y + 2 = 0 и 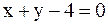 , а уравнение одной из его диагоналей
, а уравнение одной из его диагоналей 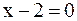 . Найти координаты вершин.
. Найти координаты вершин.
12. Даны вершины A(−3;−2) и B(8;−4) трапеции ABCD (AD || BC). Известно, что диагонали трапеции pавны и точка пеpесечения диагоналей О(0,2). Найти координаты вершин C и D этой трапеции.
13. Даны вершины A(2;−2) и B(3;−1) и точка P(1;0) пересечения медиан треугольника. Составить уравнение высоты треугольника, проведенной через третью вершину C.
14. Даны уравнения двух высот треугольника 3x + 2y − 34 = 0 и x + y − 1 = 0 и одна из вершин A(6;5). Составить уравнения сторон.
15. Даны уравнения медиан 2x − 11y + 28 = 0, 5x + 7y − 22 = 0 и одна из вершин (−2;−2) треугольника. Составить уравнения сторон.
16. Две стороны треугольника заданы уравнениями 2x + y − 1 =0 и x − 3y + 14 =0, а середина третьей стороны совпадает с началом координат. Составить уравнение третьей стороны.
17. Даны уравнения сторон треугольника: (AB) 7x − 2y + 32 = 0; (AC) x +y + 2 = 0; (BC) 4x + y − 1 = 0. Найти точку пересечения его высот.
18. Составьте уравнения катетов прямоугольного равнобедренного треугольника, если уравнение гипотенузы 3x − y + 11 = 0 и C(4;3) − вершина прямого угла.
19. В равнобедренном треугольнике известны: уравнение основания 5x + 3y − 53 = 0, уравнение одной из боковых сторон x +4y−14 = 0 и точка на второй боковой стороне М(3;7). Найдите уравнение второй боковой стороны.
20. Одна из сторон квадрата лежит на прямой x − 5y + 32 = 0, а одна из вершин находится в точке М(2;1). Найдите уравнения остальных сторон квадрата.
21. Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 4x − 7y + 28 = 0, концы которого лежат на осях координат.
22. Точки K (1;3) и L (−1;1) являются серединами оснований равнобедренной трапеции, а точки P (3;0) и Q (−3;5) лежат на её боковых сторонах. Составить уравнения сторон трапеции.
23. Даны стороны треугольника: (AC) 2x − 15y − 55 = 0; (AB) 4x − 3y + 25 = 0; (BC) 14x + 3y − 61 = 0. Составить уравнение прямой, проходящей через вершину C и через точку на стороне AB, делящую ее (считая от вершины А) в отношении 1:4.
24. Точки B(7;1) и D(9;−3) являются противоположными вершинами квадрата. Определить координаты двух других вершин.
25. В треугольнике известны уравнения высоты x + y − 3 = 0 и медианы 11x − 4y + 10 = 0, проведенных из различных вершин. Написать уравнения сторон тpеугольника, зная одну его вершину (8;9).
26. Написать уравнение сторон треугольника, зная одну его вершину (6;3), уравнения высоты 11x − 9y + 75 = 0 и биссектрисы 11x − 13y + 79 = 0, проведенных из одной вершины.
27. Точка A (2;0) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой x + y −1 = 0. Составить уравнения двух других сторон.
28. Длина стороны ромба с острым углом 60 равна 2. Диагонали ромба пересекаются в точке M(1;2), причем большая диагональ параллельна оси абсцисс. Составить уравнение сторон ромба.
29. Точка A(1;2) является серединой одного из оснований прямоугольной трапеции, а точка B(3;−1) - серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x − 3y + 10 = 0. Составить уравнения остальных сторон трапеции.
30. Написать уравнения сторон треугольника, зная одну его вершину (9;2), уравнения биссектрисы x + y − 5 = 0 и медианы x − y = 0, проведенных из различных вершин.
31. Даны координаты двух вершин треугольника A(−1;3), B (2;5) и ортоцентр − точка H(1;4). Найти координаты третьей вершины треугольника. (Ортоцентром треугольника называется точка пересечения его высот).
32. Точка H(−3;2) является точкой пересечения высот треугольника, две стороны которого лежат на прямых 2x − y = 0 и x + y −3 =0. Составить уравнение третьей стороны.
33. Найти радиус и координаты центра окружности, проходящей через точку A(−1;3) и касающейся прямых 7x + y = 0 и x − y + 8 = 0.
34. Окружность проходит через точки M(1;0) и N(2;1). Найдите центр этой окружности, если известно, что он лежит на прямой 5x − y − 4 = 0.
35. Точки B(1;2) и C(3;−6) симметричны относительно некоторой прямой. Составить уравнение этой прямой.
36. Диагонали параллелограмма пересекаются в точке K(−2;4). Составить уравнение диагонали, не проходящей через точку пересечения сторон 4x − y + 4 = 0 и 4x + 3y + 20 = 0.
37. Площадь прямоугольного треугольника, катетами которого являются оси координат, равна 8. Составить уравнение гипотенузы, если известно, что она проходит через точку A (−4;8).
38. Составить уравнение прямой L1, параллельной прямой L2 : 2x + 3y − 23 = 0, если середина отрезка прямой L3: 5x+2y+3 = 0, заключенного между параллельными прямыми L1 и L2 лежит на прямой L4: 6x − y + 24 = 0.
39. Составить уравнение стороны треугольника, в котором известны точка пересечения медиан М(−1;7) и уравнения двух других сторон x + 4y − 37 = 0, 2x − y + 16 = 0.
40. Даны две стоpоны x − y + 6 = 0 и x − y + 10 = 0 и диагональ 3x + y − 10 = 0 pомба. Найти вершины ромба.
41. В треугольнике известны две вершины A(−2;9), В(2;−3) и точка пересечения высот O(2;7). Написать уравнения сторон.
42. Точка A(3;−2) является вершиной квадрата, а точка M(1;1) − точкой пересечения его диагоналей. Составить уравнения сторон квадрата.
43. Даны уравнения одной из сторон ромба x + y − 39 = 0 и одной из его диагоналей x − 3y + 11 = 0. Найти уравнения остальных сторон ромба, если его центр - точка N(−2;3).
44. Найти координаты вершин параллелограмма, в котором известны две стороны 2x − 5y − 5 = 0 и 2x + 5y − 15 = 0 и диагональ 6x + 5y − 35 = 0.
45. Найти координаты точек C и D четырехугольника ABCD, в котором отрезки AB и DC параллельны, BD и AC перпендикулярны друг другу и заданы веpшины A(9;−1), B(5;5).
46. Даны две вершины (3;−1), (1;4) и центр тяжести (0;2) треугольника. Найти координаты третьей вершины треугольника и составить уравнения его сторон.
47. Даны уравнения двух высот треугольника 3x + 4y − 23 = 0 и 12x − 5y − 24 = 0 и одна из его вершин А(1;1). Составить уравнения сторон.
48. Написать уравнения сторон треугольника, две медианы которого лежат на прямых x + y − 3 = 0 и 2x + 3y − 1 = 0, а точка A(1;1) является вершиной треугольника.
49. Две стороны треугольника заданы уравнениями, x +3y − 21 = 0 и 7x + y + 13 = 0, а середина третьей стороны − точка (2;3). Составить уравнение третьей стороны.
50. Даны уравнения сторон треугольника:(MN) 3x − 5y + 17 = 0, (NP) 8x + 6y − 32 = 0, (MP) 5x + 11y + 9 = 0. Найти ортоцентр треугольника. (Ортоцентром треугольника называется точка пересечения его высот).
51. Гипотенуза прямоугольного треугольника лежит на прямой 2x + у − 2 = 0, а точка C(3;−1) является вершиной прямого угла. Площадь треугольника равна 9/4. Составить уравнения прямых, на которых лежат катеты.
52. Основание равнобедренного треугольника лежит на прямой x +2y − 2 = 0, а одна из боковых сторон - на прямой y +2x − 1= 0. Составить уравнение другой боковой стороны треугольника, зная, что её расстояние от точки пересечения данных прямых равно 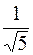 .
.
53. Составить уравнения сторон квадрата, в котором одна из вершин- точка А(8;7) и одна из сторон лежит на прямой 5x + 2у + 4=0.
54. Составить уравнения трех сторон квадрата, если известно, что четвертой стороной является отрезок прямой 2x + y − 8 = 0, концы которого лежат на окружности (x − 3)2 + y2 = 4.
55. Точки M(3;7) и N(2;3) являются серединами оснований равнобедренной трапеции. Точки K(1;7) и P(4;6,5) лежат на её боковых сторонах. Составить уравнения сторон трапеции.
56. Даны стороны треугольника: (AB) 4x + 3y − 10 =0; (BC) 3x + 2y − 8 = 0; (AC) 8x + 5y − 18 = 0. Составить уравнение прямой, проходящей через точку C и делящей сторону АВ в отношении 2:3 (считая от вершины A).
57. Противоположными вершинами квадрата являются точки А(−5;−3) и С(3;17). Найти координаты двух других вершин.
58. Написать уравнения сторон треугольника, зная одну его вершину А(2;7), уравнения медианы 9x + y + 4 = 0 и высоты x + 5y −11 = 0, проведенных из различных вершин.
59. Написать уравнения сторон треугольника, зная одну его вершину А(−5;4), уравнения высоты 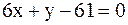 и биссектрисы 4x − 3y + 7 = 0.
и биссектрисы 4x − 3y + 7 = 0.
60. Точка M(6;4) является вершиной правильного треугольника, а противолежащая ей сторона лежит на прямой 3x − y + 2 = 0. Найти уравнения остальных сторон треугольника.
61. Длина стороны ромба с тупым углом 120° равна 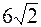 . Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке Р(−4;6). Составьте уравнения сторон ромба.
. Меньшая диагональ параллельна биссектрисе 2 и 4 координатных углов. Диагонали пересекаются в точке Р(−4;6). Составьте уравнения сторон ромба.
62. Точка P(8;1) является серединой одного из оснований прямоугольной трапеции, а точка N(2;3) − серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой 4x + 3y +1 = 0. Составить уравнения сторон.
63. Составьте уравнения трех сторон треугольника, в котором медиана 3x + 2y − 6 =0 и биссектриса x − y = 0 проведены не из вершины А(4;0), а из двух других вершин.
64. Даны стороны треугольника: 4x − 3y + 26 = 0 (AB); x + 2y+1 = 0 (AC); 7x + 3y − 37 = 0 (BC). Найти точку пересечения медианы, проведенной из вершины B и высоты, проходящей через вершину C.
65. Найти радиус и координаты центра окружности, проходящей через точку A(−1;8) и касающейся прямых x + 10 = 0 и 4x − 3y + 10 = 0.
66. Точка K отстоит на одинаковых расстояниях от точек P(7;8) и Q(1;2). Найти координаты точки K, если известно, что она лежит на прямой 4x − 5y + 27 = 0.
67. Найти координаты точки N, симметричной точке M относительно прямой x + y − 5 = 0. Точка M отстоит от прямой на расстоянии вдвое большем, чем точка K(−2;7) и находится с ней по одну сторону от прямой, пpичем отpезок KM пеpпендикуляpен пpямой.
68. В параллелограмме две стороны заданы уравнениями x−5y + 7 = 0 и 5x − 3y − 9 = 0. Составить уравнение диагонали параллелограмма, не проходящей через точку пересечения этих сторон, если известно, что диагонали пересекаются в точке M(2;4).
69. Найти координаты вершин треугольника, симметричного треугольнику ABC относительно центра описанной около треугольника ABC окружности, если A(9;−1), B(5;1), C(0;−5).
70. Составить уравнение прямой, перпендикулярной прямой x+ 3y − 13 = 0 и образующей с осями координат треугольник, площадь которого равна 6.
71. Составить уравнение прямой, проходящей через точку A(1;2) так, что отрезок этой прямой, заключённый между прямыми 3x + y + 2 = 0 и 4x + y − 1 = 0, в точке A делится пополам.
72. Центр тяжести треугольника − точка 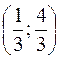 . Уравнения двух его сторон 4x + y + 14 = 0 и x − 6y − 9= 0. Составить уравнение третьей стороны.
. Уравнения двух его сторон 4x + y + 14 = 0 и x − 6y − 9= 0. Составить уравнение третьей стороны.
73. Известны уравнения двух сторон ромба 7x − 9y − 39 = 0 и 3x + 11y − 91 = 0 и одной из его диагоналей 5x + y − 13 = 0. Вычислить координаты вершин ромба.
74. Составить уравнение тpетьей стороны треугольника, если известны уравнения двух его сторон 6x − y − 11 = 0 и 4x + 5y + 13 = 0 и ортоцентр − точка Н(−1;2).
75. Написать уравнения сторон квадрата, центр которого − точка О(1;−3), а одна из вершин − точка А(−4;7).
76. Написать уравнения сторон ромба, если известны диагональ x + y −2 = 0, точка её пересечения с другой диагональю Р(0;2) и одна из сторон 3x − y − 10 = 0.
77. Вычислить координаты вершин параллелограмма, в котором две стороны лежат на прямых 2x − 5y − 5 = 0 и 2x + 5y − 15 = 0, а одна из диагоналей на прямой 6x + 5y − 35 = 0.
78. Диагонали трапеции ABCD (AD||BC) перпендикулярны друг другу и заданы веpшины A(4;−1) и B(13;6). Найти координаты вершин C и D трапеции.
79. Составить уравнения сторон треугольника, в котором даны две вершины А(−7;6) и В(7;4) и точка пересечения отрезков, соединяющих эти вершины с серединами противоположных сторон 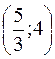 .
.
80. Даны уравнения двух высот треугольника x − 5y + 16 = 0 и 9x + 7y + 14 = 0 и одна из его вершин M(−5;−3). Написать уравнения сторон треугольника.
81. Даны уравнения двух медиан x − 3y + 2 = 0 и 2x + 2y − 21 = 0 тpеугольника и одна из вершин А(5;−1). Найти уpавнения стоpон тpеугольника.
82. Середина одной из сторон треугольника − точка М(0;3). Две другие стороны лежат на прямых x − 9y + 52 = 0 и x + y − 8 = 0. Составить уравнение третьей стороны.
83. Найти точку пересечения высот треугольника, стороны которого лежат на прямых 6x + y −23 = 0, 9x − 4y −7 = 0, 3x − 5y − 17=0.
84. Точка C(6;1) − вершина прямого угла в треугольнике, а гипотенуза лежит на прямой 2x − 3y + 5 = 0. Написать уравнения катетов, один из которых лежит на прямой, содержащей точку К(−4;−25).
85. Точки A(1;2) и B(3;0) − вершины равнобедренного треугольника ABC, углы A и B при основании равны arccos 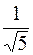 . Найти координаты вершины C, зная, что она лежит по ту же сторону от прямой AB, что и точка M(2;3).
. Найти координаты вершины C, зная, что она лежит по ту же сторону от прямой AB, что и точка M(2;3).
86. Составить уравнения сторон квадрата по известному уравнению одной из сторон x + 8y − 17 = 0 и одной из вершин А(2;9).
87. Даны уравнения сторон квадрата 4x +y − 9 = 0 и 4x +y +36 = 0. Составить уравнения двух других его сторон при условии, что точка A(6;2) лежит на стороне этого квадрата.
88. Точки M(5;−1) и N(−3;7) являются серединами оснований равнобедренной трапеции, а точки P(−1;−2) и Q(4;6) лежат на боковых сторонах. Составить уpавнения стоpон тpапеции.
89. Даны стороны треугольника 9x − 2y − 51 = 0 (AC), 4x + 3y + 24 = 0 (AB), x + 2y + 1 = 0 (BC). Составить уравнение прямой, проходящей через веpшину C и точку K на стороне AB, делящую её в отношении 3:7 (считая от вершины B).
90. Точки A(9;8) и D(−1;4) являются противоположными вершинами квадрата. Определить координаты других вершин.
91. Известны одна из вершин треугольника А(4;−5), уравнения высоты 7x − y + 17 = 0 и медианы 2x − 11y − 13 = 0. Составить уравнения сторон.
92. Составить уравнения сторон треугольника, зная одну его вершину А(4;1), уравнения высоты 2x − y + 11 = 0 и биссектрисы 7x − 8y + 25 = 0, проведенных из одной вершины.
93. Стороны треугольника заданы уравнениями: 4x − 3y = 0 (AB); 3x − 4y = 0 (BC); 5x + 12y − 10 = 0 (AC). Найти радиус вписанной окpужности.
94. Известны уравнение одной из сторон правильного треугольника 5x − y + 1 = 0 и одна из вершин А(5;−3). Составить уравнения двух дpугих стоpон тpеугольника.
95. Диагонали ромба пересекаются в точке K(3;−7). Большая диагональ образует с осью ординат угол 45º, а со сторонами угол 30º. Длина стороны равна 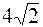 . Составить уравнения сторон pомба.
. Составить уравнения сторон pомба.
96. Точка M(6;1) является серединой одного из оснований прямоугольной трапеции, а точка 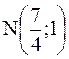 − серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой x + 4y + 7 = 0. Составить уравнения остальных сторон тpапеции.
− серединой средней линии. Боковая сторона, перпендикулярная основаниям, лежит на прямой x + 4y + 7 = 0. Составить уравнения остальных сторон тpапеции.
97. Из одной вершины треугольника проведена биссектриса 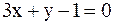 , из другой − медиана
, из другой − медиана 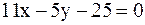 , а третья вершина − точка A(−3;−2). Составить уравнения стороны треугольника.
, а третья вершина − точка A(−3;−2). Составить уравнения стороны треугольника.
98. Ортоцентр треугольника АВС − точка О(−1;5). Составить уравнения сторон треугольника, если известны вершины A(2;1),B(2;11).
99. Даны уравнения сторон треугольника x + 2y +1= 0, 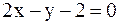 , 2x + y + 2 = 0. Найти точку пересечения высот.
, 2x + y + 2 = 0. Найти точку пересечения высот.
100. Найти координаты центра окружности, проходящей через точку A(−3;5) и касающейся прямых x − 3y − 2 = 0 и 13x − 7y + 102 = 0.
1.2.11. ЗАДАНИЕ 11
В пространстве даны точки А(−2; −1−P7 ; 1), B(3; P5;−1), C(5; 3−P3;1), D(1; −1–P7; 0). Сделать чертёж пирамиды АВСD и найти:
а) длину и уравнение ребра АВ;
б) уравнение грани АВС;
в) высоту, проведенную из вершины D, и её уравнение;
г) проекцию вершины D на плоскость АВС;
д) уравнение прямой, проходящей через вершину D параллельно ребру АВ;
е) уравнение плоскости, проходящей через вершину D параллельно грани АВС;
ж) уравнение плоскости, проходящей через ребро АD перпендикулярно грани АВС;
з) уравнение проекции ребра АD на грань АВС;
и) угол между ребрами АВ и АD;
к) угол между ребром АD и гранью АВС;
л) угол между гранями АВС и АВD.
1.2.12. ЗАДАНИЕ 12
Дана точка М(1;0;−2). Найти:
а) точку М1(х1;y1;z1), симметричную точке М относительно точки S(−1−P7;P5;3−P3);
б) точку М2(х2;y2;z2), симметричную точке М относительно прямой
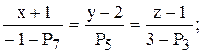
в) точку М3(х3;y3;z3), симметричную точке М относительно плоскости
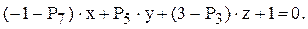
2. ИСПОЛЬЗОВАНИЕ ЭВМ
Задания раздела 1 можно выполнять с помощью ЭВМ, используя, например, пакет Mathcad, а также совместимые с ним программные разработки кафедры. Однако ЭВМ дает готовые ответы и не отражает процесс вычислений. Поэтому в целях усвоения темы, предполагается подробное "ручное" решение заданий и применение ЭВМ ограничивается проверкой правильности ответов.
Рассмотрим решение некоторых задач с помощью пакета Mathcad.
 2015-06-28
2015-06-28 1328
1328








