Контрольная работа №2

(только для студентов заочной формы, со сроком обучения 5 лет)

Вариант 1

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями и .

4. Найти несобственный интеграл .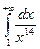

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) 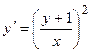; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .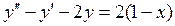

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .

9. Производительность предприятия за первый квартал выросла на 25 %, за второй тоже на 25%, а за третий упала на 20 процентов. Как должна измениться производительность за четвертый квартал, чтобы за год она увеличилась в 1,5 раза?

10. Исследовать на сходимость числовые ряды: а) ; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 2

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями ; ; x = 2

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

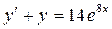6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .

9. Сколько творога жирностью 15,5% получится из 1 тонны молока жирностью 5 %, если жирность сыворотки 0,5 %?

10. Исследовать на сходимость числовые ряды: а) ; б) .

11. Найти радиус, интервал и область сходимости ряда: .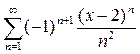

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 3

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .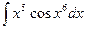

2. Найти определённые интегралы: а) 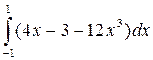; б) .

3. Найти площадь фигуры, ограниченной линиями и

4. Найти несобственный интеграл .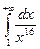

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) 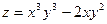; б) .

8. Исследовать на экстремум .

9. За год количество акций у Иванова удвоилось, а цена каждой акции возросла на 17 процентов. На сколько процентов увеличилась их общая стоимость?

10. Исследовать на сходимость числовые ряды: а) 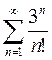; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 4

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями ; и осью ординат.

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .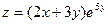

8. Исследовать на экстремум .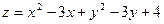

9. В банк положен вклад под 10 % годовых. Через год положили 20 % первоначальной суммы. Какая сумма (в процентах от первоначальной) будет на счете через 3 года?

10. Исследовать на сходимость числовые ряды: а) ; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 5

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиям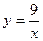и и .

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .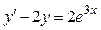

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .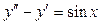

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .

9. Магазин купил товар на 40 % дороже цены, проставленной на упаковке, а продал на 50 процентов дороже этой цены. Каков процент полученной прибыли?

10. Исследовать на сходимость числовые ряды: а) 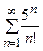; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 6

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями и .

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .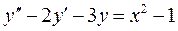

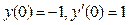7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .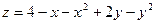

9. В банк было положено 20 000 рублей. Через год взяли 10 000 рублей. Еще через год на счете было 16 800 руб. Сколько процентов в год начисляет банк?

10. Исследовать на сходимость числовые ряды: а) ; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 7

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями ; ;

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) 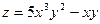; б) .

8. Исследовать на экстремум .

9. Стипендия увеличивалась дважды, причем во второй раз процент надбавки был в 1,8 раза больше, чем в первый. Кроме того, в связи с инфляцией, стипендия была проиндексирована на 20 %, после чего её абсолютный размер вырос до 342 % по сравнению с исходной величиной. Найти процент первой надбавки.

10. Исследовать на сходимость числовые ряды: а) ; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 8

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиям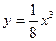и ; и ;

4. Найти несобственный интеграл .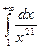

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .

9. Магазин купил товар на 35 % дешевле, чем проставленная на упаковке цена, а продал на 25 % дешевле. Каков процент полученной прибыли? (Результат округлите до десятых).

10. Исследовать на сходимость числовые ряды: а) ; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 9

1. Найти неопределённый интеграл и проверить результат дифференцированием

а) ; б) ; в) .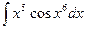

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями и .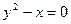

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) ; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .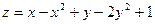

9. Фермер получил кредит в банке под определенный процент годовых. Через год фермер внес в счет погашения кредита от суммы, которую он должен был банку к этому времени, а еще через год он полностью погасил кредит, внеся в банк сумму, на 21 % превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?

10. Исследовать на сходимость числовые ряды: а) 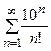; б) .

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл , взяв три члена разложения функции .

Вариант 10

1. Найти неопределённый интеграл и проверить результат дифференцированием

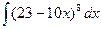а) ; б) ; в) .

2. Найти определённые интегралы: а) ; б) .

3. Найти площадь фигуры, ограниченной линиями и .

4. Найти несобственный интеграл .

5. Указать типы дифференциальных уравнений 1-ого порядка и найти их общее решение: а) 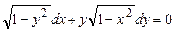; б) .

6. Найти решение дифференциального уравнения, удовлетворяющее указанным начальным условиям: ; .

7. Найти частные производные 1 и 2 порядка для функций а) ; б) .

8. Исследовать на экстремум .

9. Прирост продукции завода в первый год составил 10 %. Каков должен быть прирост продукции во второй год, чтобы за 2 года ежегодный прирост составил 20 %?

10. Исследовать на сходимость числовые ряды: а ) ; б) .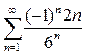

11. Найти радиус, интервал и область сходимости ряда: .

12. Приближённо вычислить интеграл 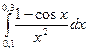, взяв три члена разложения функции .

Демонстрационный вариант контрольной работы №2

Задание №1. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.

а) , б) , в)

Задание №2. Найти определённые интегралы:

а) , б) .

Задание №3. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

.

Задание №4. Найти несобственный интеграл .

Задание № 5. Указать тип дифференциального уравнения первого порядка и найти его общее решение: а) ; б) .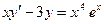

Задание №6.. Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее заданным начальным условиям:

; , .

Задание №7. Найти частные производные первого и второго порядка функций:

а) б) .

Задание №8. Исследовать на экстремум функцию .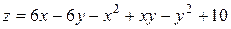

Задание №9. Число 21,6 трижды увеличивали на одно и тоже число процентов, а затем трижды уменьшали на то же самое число процентов. В результате получилось число 6,4. На сколько процентов увеличили, а затем уменьшили число?

Задание №10. Исследовать на сходимость числовые ряды:

а) ; б) .

Задание № 11. Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала сходимости.

Задание №12. Вычислить приближённо определённый интеграл, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Результат должен быть получен с точностью до 0,001.

Решение демонстрационного варианта контрольной работы № 2

Решение задачи 1

а)

.

б) I способ: подведение под знак дифференциала

.

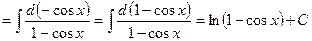II способ: метод подстановки

=

Проверим результат дифференцированием: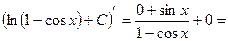

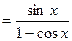. Получили подынтегральную функцию, что и требовалось доказать (ч.т.д.).

в) = 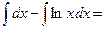для вычисления интеграла воспользуемся методом интегрирования по частям

Проверим результат дифференцированием:

. Получили подынтегральную функцию, ч.т.д.

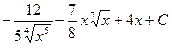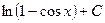Ответ: а) , б) , в) .

Решение задачи 2

а)

Решение.

.

б)

Решение.

.

Ответ: а) , б) .

Решение задачи 3

Сделаем чертёж фигуры:

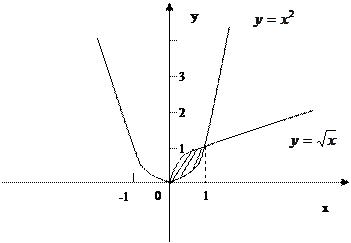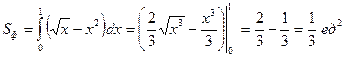
Ответ: 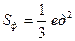; см. рис..

Решение задачи 4

Решение. По определению несобственного интеграла находим:

.

Ответ: .

Решение задачи 5

а) - это уравнение с разделяющимися переменными.

Разделим переменные, т.е. получим уравнение .

Интегрируем обе части полученного уравнения

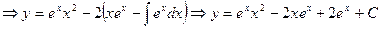- общее решение.

б) - это линейное дифференциальное уравнение 1 – ого порядка.

Первый способ: метод подстановки. Пусть , тогда . Подставив в исходное уравнение, получим . Группируем таким образом, чтобы в скобках была только одна функция или 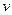, т.е. (можно ). Далее выбираем функцию 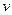так, чтобы выражение в скобках обращалось в нуль, т.е.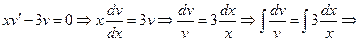

.

Подставим найденное в уравнение , получим .

Общее решение уравнение .

Второй способ. Метод вариации произвольной постоянной. Предварительно решаем линейное уравнение .

Затем решение исходного уравнения ищем в виде , т.е. заменяем константу неизвестной функцией. Подставляем это решение в уравнение, получим

.

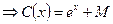Искомое общее решение уравнение .

Ответ: .

Решение задачи 6

; , .

- это неоднородное дифференциальное уравнение 2 – ого порядка с постоянными коэффициентами .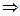

Рассмотрим однородное уравнение . Соответствующее характеристическое уравнение имеет вид ,

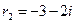. Следовательно, - общее решение однородного уравнения.

Частное решение неоднородного уравнения будем искать в виде .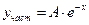

Имеем .

Подставим эти значения в неоднородное уравнение

Итак, - общее решение.

Найдём частное решение:

.

Итак, найдём частное решение .

Ответ: ; .

Решение задачи 7

Ответ: ; ; ; ; ;

.

Решение задачи 8

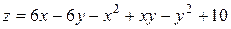
Найдем частные производные функции:

,

.

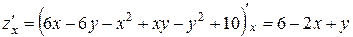Найдем критические точки функции из системы Û

Û Û . Решаем полученную систему по формулам Крамера: , , 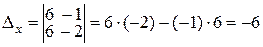. Далее, , . Следовательно, (2;-2) – единственная критическая точка.

Далее находим частные производные второго порядка: ,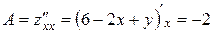

,

.

Имеем . Значит, в точке (2;-2) имеется экстремум; кроме того, А <0, поэтому (2;-2) – точка максимума.

Находим максимум функции

.

Решение задачи 9

Для решения этой задачи используем формулу сложных процентов:

В результате получаем следующее выражение:

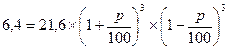
или

отсюда ,

извлекая корень третьей степени из левой и правой частей, получим:

или .

Извлекая квадратный корень из обеих частей, получим: , отсюда .

Ответ: на 57,7 %

Решение задачи 10

а)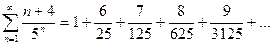

Это положительный числовой ряд, можно применить один из пяти достаточных признаков сходимости.

Проверяем сходимость ряда по признаку Даламбера. Т.к. общий член ряда , то, заменяя в выражении n – го члена n на n+1, находим

. Затем ищем предел отношения последующего члена к предыдущему при

.

Итак, , следовательно, ряд сходится.

б)

Это знакочередующийся ряд. Воспользуемся признаком Лейбница. Для этого нам надо показать, что

1) члены ряда по модулю убывают, т.е.

2)

Проверим эти условия:

1)

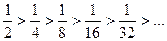, т.е. первое условие выполняется.

2) 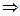выполняется второе условие.

Итак, условия 1, 2 выполняются, следовательно, ряд сходится.

Выясним, сходится он абсолютно или условно, для этого исследуем ряд, составленный из модулей : - бесконечно убывающая геометрическая прогрессия 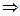ряд сходится 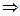исходный ряд сходится абсолютно.

Ответ: а) ряд сходится; б) ряд сходится абсолютно.

Решение задачи 11

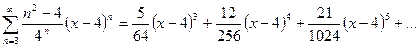
Решение: Это степенной ряд в точке х=4, где .

Радиус сходимости находим по формуле .

Интервал сходимости данного ряда определяется неравенством или .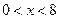

Исследуем концы интервала сходимости. При получаем числовой ряд

- знакочередующийся числовой ряд.

Очевидно, ряд расходится, т.к. 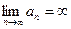, т.е. не выполняется необходимый признак сходимости 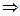х=0 не принадлежит области сходимости.

При получаем числовой ряд . Этот ряд тоже расходится, т.к. 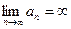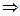х=8 не принадлежит области сходимости.

Ответ: радиус сходимости равен 4; интервал сходимости .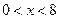

Решение задачи 12

Вычислить с точностью до 0,001

Разложим подынтегральную функцию в степенной ряд

=

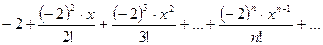
Подставим в интеграл вышеприведённое разложение подынтегральной функции и, почленно интегрируя в указанных пределах, получаем:

.

Уже третий член меньше 0,001. Поэтому для вычисления приближённого значения интеграла с требуемой точностью достаточно ограничиться первыми двумя членами ряда:

.

Ответ: -0,19.