ГЛАВА 1
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ОБУЧЕНИЯ ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ. ПОНЯТИЕ ТЕОРЕМЫ. ОСНОВНЫЕ ВИДЫ ТЕОРЕМ И ИХ СТРУКТУРА
Структуру отдельных мыслей и способы их сочетаний называют формами мышления. С точки зрения формальной логики мышление характеризуется тремя основными формами: понятиями, суждениями, умозаключениями.
Примеры понятий:
1. Треугольник — это фигура, состоящая из трех отрезков, попарно соединяющих три точки, не лежащие на одной прямой.
2. Арифметическим квадратным корнем из числа Q называется неотрицательное число, квадрат которого равен Q.
Примеры суждений:
1. Каждая прямая разделяет плоскость на две полуплоскости; любые две точки одной и той же полуплоскости лежат по одну сторону от этой прямой, а любые две точки разных полуплоскостей лежат по разные стороны от нее.
2. Через любые две точки проходит прямая, и притом только одна.
Примеры умозаключений:
1. Если a>b, b>c то а>с.
2. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
|
|
|
Следует заметить, что на вопрос «Чем являются те или иные утверждения: теоремами, аксиомами или определениями?» нельзя ответить однозначно вне контекста какого-нибудь курса математики. Так, например, утверждение «Через точку вне прямой можно провести единственную прямую, параллельную данной прямой» в одном курсе геометрии может быть аксиомой, в другом — теоремой. Возможен, например, вариант, когда в каком-либо курсе геометрии за аксиому принято утверждение, называемое в нашем школьном курсе геометрии теоремой Пифагора.
Перейдем к рассмотрению понятия теоремы, ее структуры и видов теорем.
Математическое предложение, истинность которого устанавливается посредством доказательства, называют теоремой.
Название «теорема» происходит от греческого слова θε?ρημα — представление, зрелище (так как в древности часто теоремы доказывались публично, на площадях, и они носили характер спора, диспута).
В школьном курсе математики для словесной формулировки теоремы используются три формы суждения:
1) Категорическая.
Пример 1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Пример 2. Постоянный множитель можно вынести за знак производной: (cf(x))' = cf'(x).
2) Условная.
Пример 1. Если в треугольнике два угла равны, то треугольник равнобедренный.
Пример 2. Если F'(x)=0 на некотором промежутке, то на этом промежутке F(x) = C, где С — постоянная.
3) Разделительная.
Пример 1. Плоскость и не лежащая на ней прямая либо не пересекаются, либо пересекаются в одной точке.
Пример 2. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.
|
|
|
Теоремы категорической и разделительной форм можно переформулировать, используя словосочетание «если... то...», т. е. обратить ее формулировку в условную. Пусть, например, дана теорема: «В ромбе диагонали взаимно перпендикулярны». В условной форме формулировка этой теоремы будет выглядеть так: «Если четырехугольник является ромбом, то его диагонали взаимно перпендикулярны».
Заметим, что разбор структуры теоремы более доступен для учащихся в том случае, когда она сформулирована в условной форме.
Условная форма теоремы может быть эффективно использована и для того, чтобы дать ответ на вопрос: «О свойстве или о признаке идет речь в теореме?» На этот вопрос легко ответить, если теорему сформулировать в условной форме. Если окажется, что рассматриваемое понятие находится в условии теоремы, то теорема выражает свойство этого понятия, если же понятие находится в заключении теоремы, то она выражает признак. Покажем это на примерах.
1. Теорема Пифагора: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Переформулировав теорему из категоричной формы в условную, будем иметь: «Если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов катетов». Поскольку понятие «прямоугольный треугольник» находится в условии теоремы, то она выражает собой свойство этого понятия.
2. Теорема: «В равнобедренном треугольнике углы при основании равны».
Сформулируем теорему в условной форме. Будем иметь: «Если треугольник равнобедренный, то углы при основании равны». Поскольку понятие «равнобедренный треугольник» находится в условии, то эта теорема выражает свойство объекта.
3. Теорема: «Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны».
Понятие «параллельные прямые» находится в заключении теоремы, а значит, это теорема-признак.
4. Теорема: «Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны».
Это теорема-признак, ибо понятие «подобные треугольники» находится в заключении теоремы.
Рассмотрим в связи с этим еще один пример.
Теорема: «Если трапеция равнобокая, то:
1) углы при одном и том же основании равны;
2) высоты, проведенные из концов одного основания на другое основание, равны;
3) перпендикуляр, опущенный из точки пересечения продолжения боковых сторон на основания, делит основания трапеции пополам».
Сформулируем предложения, обратные данным свойствам:
1°) если в трапеции углы при одном и том же основании равны, то она является равнобокой;
2°) если в трапеции высоты равны, то она является равнобокой;
3°) если в трапеции перпендикуляр, опущенный из точки пересечения продолжений боковых сторон на основания, делит их пополам, то она является равнобокой.
Если сопоставить умозаключения 1—3 и 1°—3°, то можно заметить, что по свойствам понятия можно судить о его признаках. Для этого поступают следующим образом. Чтобы из свойства понятия получить признак этого понятия, надо построить предложение, обратное свойству, и проверить его истинность. Если полученное предложение ложно, то оно не может являться признаком. Так, в нашем примере умозаключения 1° и 3° являются признаками равнобедренной трапеции, а умозаключение 2° признаком не является.
В школьном курсе математики формулируются и доказываются теоремы, имеющие различный вид: в одних теоремах из одного условия вытекает одно заключение, в других — из одного условия вытекает несколько заключений, в третьих — из нескольких условий вытекает одно заключение и т. д.
|
|
|
Но в любом случае теорема состоит из трех частей:
1) разъяснительная часть, где описывается множество 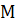 объектов, о которых идет речь в этой теореме;
объектов, о которых идет речь в этой теореме;
2) условие теоремы, т. е. некоторый предикат 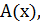 заданный на множестве
заданный на множестве 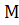 ;
;
3) заключение теоремы — некоторый предикат 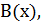 заданный на том же множестве
заданный на том же множестве 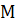 .
.
В символах математической логики теорема может быть записана следующим образом: 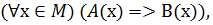 где
где
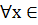 M — разъяснительная часть теоремы;
M — разъяснительная часть теоремы;
А(х) — условие теоремы; В(х) — заключение теоремы.
Часто в литературе используется такая терминология:
- тезис — доказываемое утверждение;
- аргументы (основания доказательства) — используемые в доказательстве уже известные утверждения, из которых обязательно следует истинность доказываемого тезиса;
- демонстрация — последовательность расположения аргументов и выводов, образующих цепь умозаключений.
При доказательстве тезис должен удовлетворять следующим требованиям: быть ясным и точно определенным; оставаться тождественным, т. е. одним и тем же, на протяжении всего доказательства; не должен содержать в себе логического противоречия; не должен находиться в логическом противоречии с суждениями по данному вопросу, высказанными ранее; определять собой ход доказательства так, чтобы то, что в результате будет доказано, было бы именно тем, что требовалось доказать.
Требования к аргументам доказательства таковы: они должны быть истинными предложениями данной теории; быть достаточным основанием для доказываемого предложения; быть предложением, истинность которого доказана самостоятельно, независимо от доказываемого предложения; из совокупности суждений, составляющих аргументы, обязательно должна следовать истинность тезисов.
Разберем структуру на примере теоремы из курса геометрии 8 класса: «Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы».
Данную теорему после выбора обозначений можно записать в такой форме: (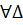 ABC,
ABC, 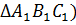 (
( А=∠
А=∠ 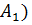 => (
=> (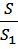 =
= 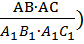 .
.
|
|
|
Разъяснительная часть теоремы выделяется из условия и заключения теоремы путем установления природы объектов и их множеств, на которых рассматриваются условие и заключение, и в данном случае она состоит в том, что рассматриваются любые пары треугольников.
 А=∠
А=∠ 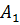 — условие теоремы;
— условие теоремы; 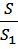 =
= 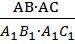 — заключение теоремы.
— заключение теоремы.
Абсолютное большинство теорем (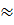 60%) в школьном курсе геометрии в символах математической логики может быть записано следующим образом: (
60%) в школьном курсе геометрии в символах математической логики может быть записано следующим образом: (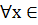 M) (А(х)
M) (А(х) 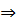 В(х)).
В(х)).
Предикаты А(х) и В(х) входящие в теорему, могут иметь сложную структуру, и отсюда возникают теоремы различной логической конструкции. Приведем пример: «В ромбе диагонали перпендикулярны друг другу и делят углы при вершинах ромба пополам». Эта теорема символически может быть записана так: (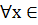 M) (А(х)
M) (А(х) 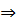
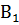 (х)
(х) 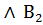 (х)). где М — множество четырехугольников;
(х)). где М — множество четырехугольников; 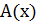 — предикат «четырехугольник
— предикат «четырехугольник 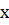 является ромбом»;
является ромбом»; 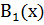 — предикат «в четырехугольнике
— предикат «в четырехугольнике 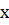 диагонали перпендикулярны»;
диагонали перпендикулярны»; 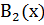 — предикат «в четырехугольнике
— предикат «в четырехугольнике 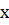 диагонали делят углы при вершинах пополам».
диагонали делят углы при вершинах пополам».
Помимо теорем вида 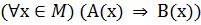 в математике встречаются и теоремы другого вида.
в математике встречаются и теоремы другого вида.
Пример 1. 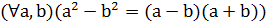 .
.
Знак 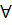 показывает, что это соотношение является тождеством. Эта теорема имеет следующую форму:
показывает, что это соотношение является тождеством. Эта теорема имеет следующую форму: 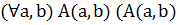 — некоторый предикат, записанный в виде равенства).
— некоторый предикат, записанный в виде равенства).
Пример 2. Теорема существования может быть записана в такой форме: (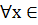 M) (
M) (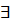 y) (А(х, у)).
y) (А(х, у)).
Примерами теорем существования могут служить следующие теоремы из школьного курса геометрии 7—11 классов:
а) через любую точку проходит прямая, перпендикулярная к данной прямой, и притом только одна;
б) около любого треугольника можно описать окружность, и притом только одну;
в) через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Можно еще указать такие формализованные структуры теорем:
1) (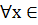 M) (
M) (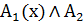 (x)
(x) 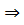 В(х));
В(х));
2) (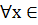 M) (А(х)
M) (А(х) 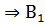 (х)
(х) 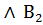 (х));
(х));
3) (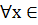 M) (А(х)
M) (А(х) 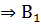 (х)
(х) 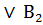 (х));
(х));
4) (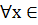 M) (
M) (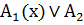 (x)
(x) 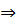 В(х));
В(х));
5) (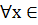 M) (A(x)
M) (A(x) 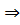 (C(x) ⇒ D(x));
(C(x) ⇒ D(x));
6) (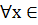 M) ((C(x)
M) ((C(x) 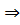 D(x))
D(x)) 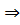 B(x));
B(x));
7) (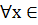 M) (
M) (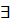 y A(x, y)
y A(x, y) 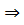 B(x, у));
B(x, у));
8) (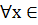 M) (
M) ( y A(x, y)
y A(x, y) 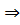 B(x, у)) — теорема существования и единственности.
B(x, у)) — теорема существования и единственности.
С любой теоремой обычно связаны еще три теоремы. Приведем все четыре вида теорем:
1) (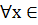 M) (А(х)
M) (А(х) 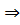 В(х)) — прямая теорема;
В(х)) — прямая теорема;
2) (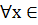 M) (В(х)
M) (В(х) 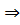 А(х)) — обратная теорема;
А(х)) — обратная теорема;
3) (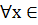 M) (
M) (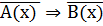 ) — противоположная теорема;
) — противоположная теорема;
4) (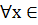 M) (
M) (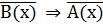 ) — теорема, обратная противоположной (контрапозитивная).
) — теорема, обратная противоположной (контрапозитивная).
Рассмотрим все эти виды теорем на примерах.
Пример 1.
1) Если четырехугольник — параллелограмм, то диагонали его, пересекаясь, делятся пополам. (Истинно.)
2) Если в четырехугольнике диагонали, пересекаясь, делятся пополам, то этот четырехугольник — параллелограмм. (Истинно.)
3) Если четырехугольник не параллелограмм, то его диагонали, пересекаясь, не делятся пополам. (Истинно.)
4) Если в четырехугольнике диагонали, пересекаясь, не делятся пополам, то такой четырехугольник не параллелограмм. (Истинно.)
Пример 2.
1) Если углы вертикальные, то они равны. (Истинно.)
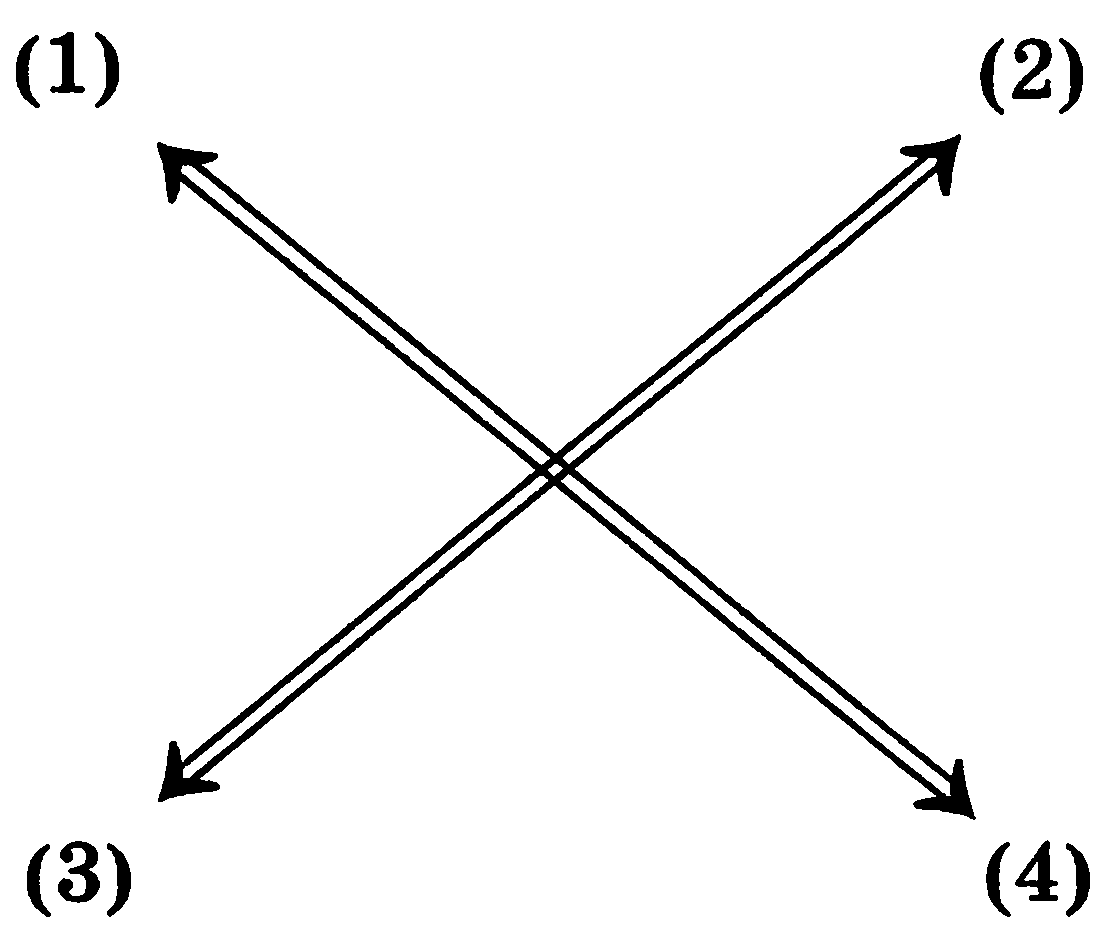
Рис. 1
2) Если углы равны, то они вертикальные. (Ложно.)
3) Если углы не вертикальные, то они не равны. (Ложно.)
4) Если углы не равны, то они не вертикальные. (Истинно.)
Между прямой, обратной, противоположной и контрапози- тивной теоремами существует тесная связь, которую символически можно выразить так, как показано на рисунке 1.
Прямая и обратная противоположной теоремы эквивалентны, т. е. они одновременно истинны или ложны.
Обратная и противоположная теоремы эквивалентны, т. е. они одновременно истинны или ложны.
Такая связь между теоремами показывает нецелесообразность изучения всех четырех теорем; достаточно установить истинность или ложность какой-либо одной логически неравносильной пары теорем, так как истинность или ложность одной пары влечет за собой истинность или ложность другой пары теорем. В связи с этим в любом курсе математики встречаются лишь прямая и обратная теоремы.
Обращаем внимание на тот факт, что если прямая и обратная теоремы верны, то можно записать их в виде одной, употребляя словосочетание «тогда и только тогда» или «в том и только в том случае».
Приведем примеры.
Прямая теорема: «Если внутренние накрест лежащие углы равны, то прямые параллельны». (Теорема верна.)
Обратная теорема: «Если прямые параллельны, то внутренние накрест лежащие углы равны». (Теорема верна.)
Эти две теоремы можно сформулировать в одной из следующих форм:
а) Две прямые параллельны тогда и только тогда, когда накрест лежащие углы равны.
б) Накрест лежащие углы равны тогда и только тогда, когда прямые параллельны.
в) Две прямые параллельны в том и только в том случае, если накрест лежащие углы равны.
г) Накрест лежащие углы равны в том и только в том случае, если прямые параллельны.
В качестве примера может служить теорема Пифагора, которая в некоторых курсах геометрии формулируется так: «Сумма квадратов двух сторон треугольника равна квадрату третьей стороны тогда и только тогда, когда треугольник прямоугольный». В этой формулировке содержится, по существу, две теоремы:
а) Если треугольник прямоугольный, то сумма квадратов двух его катетов равна квадрату гипотенузы.
б) Если в треугольнике сумма квадратов двух сторон равна квадрату третьей стороны, то треугольник прямоугольный.
Заметим, что если условие прямой теоремы сложное (состоит из нескольких частных условий), то можно сформулировать для данной теоремы несколько обратных. В общем виде это выглядит так. Если прямая теорема имеет, например, вид: «Если А, В и С, то D», то обратными ей являются такие теоремы:
— если D, то А, В и С;
— если А и D, то В и С;
— если В и D, то А и С;
— если D, В и С, то А;
— если A, D и С, то В и т. д.
Приведем пример, рассмотрев такую прямую теорему:
«Если треугольник ABC равнобедренный и BD — его медиана, то она является и высотой».
Обратными этой теореме будут, например, такие теоремы:
— если треугольник ABC равнобедренный и BD его высота, то она является и медианой;
— если в треугольнике ABC отрезок BD является высотой и медианой, то этот треугольник равнобедренный.
 2015-05-20
2015-05-20 18019
18019







