Обработка результатов измерений

ОЗУ и ПЗУ

Запоминающие устройства классифицируются на:

- СОЗУ – сверхоперативная память, служит для обмена информацией микропроцессора с внешними запоминающими устройствами и хранения промежуточных данных и команд. Быстродействие соизмеримо с быстродействием микропроцессора. Выполняется на полупроводниковых приборах, причём основой является ТТЛШ- или ЭСЛ-технология.

- ОЗУ. Быстродействие на порядок ниже, чем у СОЗУ, но объём достигает сотен килобайт. Технология изготовления – как у СОЗУ.

- ПЗУ – может быть как внутренним по отношению к микропроцессорной системе, так и внешним. Внутренние ПЗУ строится по полупроводниковой технологии и делятся на программируемые (ПЗУ) и перепрограммируемые(ППЗУ). В программируемые ПЗУ информацию можно записать только 1 раз. Формирование кода хранимой информации осуществляется пережиганием перемычек диодных матриц. Это производится подачей высокого напряжения на соответствующие ячейки (~30В). ППЗУ имеют возможность получать информацию несколько сот раз. Ограничение количества циклов перепрограммирования связано с изменением структуры p-n переходов при воздействии ультрафиолетового излучения (во время стирания ранее записанной информации). Быстродействие внутреннего ПЗУ соизмеримо с быстродействием ОЗУ. Внешнее ПЗУ может выполняться как по полупроводниковой технологии, так и на магнитных дисках, лентах и перфолентах. Внешнее ПЗУ в зависимости от типа исполнения имеют различное быстродействие и обладают различным объёмом памяти.

В основе принципа действия ПЗУ – накопителя на магнитном диске положена доменная структура строения ферромагнитного материала. В качестве носителя информации используются магнитомягкие ферромагнитные материалы с очень малой остаточной магнитной индукцией. Под воздействием внешнего магнитного поля магнитной головки происходит переориентация домена, находящегося в зоне действия магнитного поля. Его ориентация сохраняется бесконечно долго при отсутствии внешнего магнитного воздействия. При считывании информации на считывающей головке индуцируется ЭДС, которая пропорциональна углу между проводником головки и направлением магнитной индукции домена.

Для получения оценки измеряемой величины, максимально близкой к истинному значению, необходимо по экспериментальным данным найти оценку математи­ческого ожидания отдельных результатов наблюдений, оценить систематическую погрешность и исключить ее из оценки математического ожидания.

Точность оценки математического ожидания ряда наблюде­ний зависит от количества выполненных измерений и от диспер­сии случайной составляющей погрешности. Поэтому по экспери­ментальным данным оценивается не только математи­ческое ожидание, но и дисперсия.

Оценкой математического ожидания случайной величины по результатам отдельных наблюдений х ₁, x₂,..., х_п этой величины является среднее арифметическое:

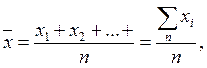(4.2.1)

где п — число наблюдений величины х.

Дисперсия суммы (разности) случайных величин определя­ется выражением

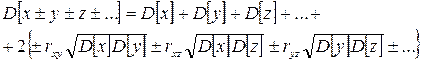
где r_xy, r_xz, r_xy,... — коэффициенты корреляции соответствующих пар ху, xz, yz... случайных величин, входящих в рассматривае­мую сумму (разность) этих величин.

При ограниченном числе измерений, результатявляется случайной величиной, основные характеристики которой (математическое ожидание и дисперсия) полу­чают на основании

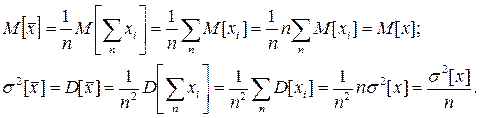(4.2.2)

Оценку дисперсии случайной величины х по результатам отдельных наблюдений х₁, х₂,..., х_п этой величины находят по формуле

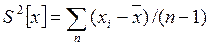(4.2.3)

Оценка среднего квадратического отклонения случайной ве­личины х равна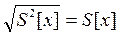

При неограниченно большом числе наблюдений оценки S² [х] и S [х] стремятся, соответственно, к s² [х] и s [х] При ограничен­ном п эти оценки являются случайными величинами.

Оценка случайной составляющей погрешности результатов измерений осуществлялась в соответствии с приведенными выше правилами.

Для обнаружения систематической погрешно­сти, природа которой неизвестна, необходима постановка специ­ального эксперимента для измерения искомой величины того же размера с использованием более точных методов и средств изме­рений. Сравнение результатов измерения х₁ и х₂, полученных в первом и во втором (более точном) эксперименте, позволяет оце­нить систематическую погрешность первого эксперимента. Если результат измерения х₁ содержит только постоянную системати­ческую погрешность, то она может быть оценена по однократ­ным результатам измерения х₁ и x₂ как 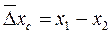. Погреш­ность этой оценки определяется погрешностью результата изме­рения х₂.

Результат измерения х₁ кроме систематической погреш­ности содержит и случайную составляющую погрешности, поэтому 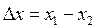— случайная величина, математическим ожиданием которой является систематическая погрешность

.

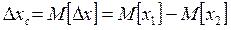Погрешность этой оценки определяется погрешностью оценок математических ожиданий результатов измерения в экспериментах.

Если причины возникновения систематической погрешности известны, то в первую очередь необходимо постараться исклю­чить или уменьшить влияние этих причин. При невозможности устранения источников погрешности необходимо на основании теоретического анализа или путем постановки специальных экс­периментов получить количественные оценки систематических погрешностей. Например, путем предварительной поверки ис­пользуемых средств измерений выявляется систематическая погрешность этих средств при разных значениях измеряемой величины. Анализируя влияние внешних факторов, можно соста­вить таблицы или графики зависимости систематической погреш­ности от внешних факторов. В этом случае для введения поправки на систематическую погрешность необходимо в процессе измере­ния контролировать значение соответствующего влияющего внешнего фактора. Существуют и другие приемы, позволяющие путем постановки специальных экспериментов либо учесть, либо исключить систематическую погрешность, не производя ее количественной оценки /Б.Я. Авдеев и др. Основы метрологиии и электрические измерения.: Л. «Энергоатомиздат», 1987. – 480 с/.

Прямые измерения. Предположим, что при многократном измерении интересующей нас величины получены п отдельных результатов наблюдений. Исключив систематическую погреш­ность из каждого наблюдения, получаем исправленный ряд зна­чений х₁, x ₂,..., х_п, математическим ожиданием которого является истинное значение измеряемой величины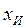. За действительное значение измеряемой величины принимаем среднее арифметиче­ское, определяемое по формуле (4.2.1), в которой x_i — исправ­ленное значение ряда наблюдений.

Для контроля правильности подсчета 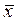использовано свой­ство - алгебраическая сумма остаточ­ных погрешностей равна нулю, т. е. 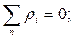где r_i = x_i — х - остаточные погрешности - отклонения между отдельными значениями наблюдений и средним арифметическим

Когда дисперсия s² полученного ряда наблюдений известна из предыдущих экспериментов или из технической документации на применяемые средства измерений, тогда дисперсия среднего ариф­метического на основании выражения (4.2.2) 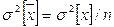, где s² [х] — дисперсия исправленного ряда наблюдений; s² [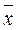] - дис­персия действительного значения (среднего арифметического) измеряемой величины этого ряда.

Если дисперсия ряда неизвестна, то на основании соотноше­ния (4.2.3) ее оценивают по формуле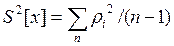

где r_i – остаточные погрешности исправленного ряда наблюдений. В этом случае за оценку дисперсии действительного значения измеряемой величины принимают

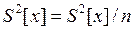. (4.2.4)

Для нахождения доверительного интервала погрешности измерения необходимо найти закон распределения для величины

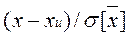(4.2.5)

при известной дисперсии или для величины

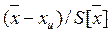(4.2.6)

при неизвестной дисперсии.

Так как в выражение (4.2.5) входит только одна случайная величина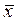, то вид закона распределения величины, определяемой этим выражением, определяется видом закона распределения величины х. При нормальном законе распределения отдельных результатов 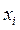закон распределения 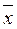тоже нормальный. Таким образом, при нормальном законе распределения случайная величина z, определяемая выражением (4.2.5), имеет нормальный закон распределения с математическим ожиданием равным нулю и дисперсией равной единице.

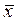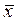Выражение (4.2.6) содержит две случайные величины и S [], поэтому закон распределения величины, определяемой этим выражением, отличается от закона распределения величи­ны, определяемой выражением (4.2.5). При нормальном законе распределения случай­ная величина t, определяемая выражением (4.2.6), имеет закон распределения Стьюдента. Для таких функций z_pи t_p(f) существуют таблицы, по которым можно найти значения, определя­ющие с доверительной вероятностью P границы доверительного интервала. Число f - число степеней свободы и в данном случае .

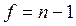Чем больше число измерений в ряду наблюдений, тем ближе оценка S [х] совпадает с действительным средним отклонением s [х]. Следовательно, с увеличением числа на­блюдений закон распределения Стьюдента приближается к нор­мальному закону. Практически при .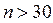

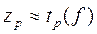Зная z _р или t_p (f), на основании выражений (4.2.5) и (4.2.6) с учетом (4.2.2) и (4.2.4), результат измерения с доверительной вероятностью Р можно записать в виде

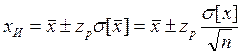(4.2.7)

при известной дисперсии или в виде

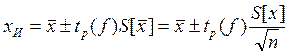(4.2.8)

при неизвестной дисперсии.

Если закон распределения отдельных результатов измерения x_i отличается от нормального, то найти закон распределения случайных величин, определяемых выражениями (4.2.5) и (4.2.6) затруднительно. В этом случае пользуются следую­щей рекомендацией: закон распределения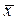с увеличением числа наблюдений стремится к нормальному закону. Практически при n > 5 можно считать, что закон распределения х близок к нор­мальному закону и при известном s[х] для приближенной оцен­ки доверительного интервала можно пользоваться выражением (4.2.7). Если дисперсия s ²[х] неизвестна, то необходимо уве­личить число наблюдений n, так чтобы оценка S [х] была близ­ка к s [х]. Практически это условие выполняется при n > 30. В этом случае для приближенной оценки доверительного интер­вала можно также пользоваться выражением (4.2.7).

Если ряд наблюдений х₁, х₂,..., х_п содержит результат x_k, существенно отличающийся от остальных, то необходимо прове­рить, не является ли он промахом. При нормальном законе рас­пределения отдельных результатов измерения x_i обнаружение промаха сводится к проверке неравенства

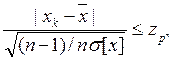(14-15)

при известной дисперсии или

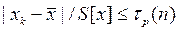(14-16)

при неизвестной дисперсии.

В этих выражениях Р — вероятность, с которой обнаружива­ется промах; 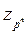— граница доверительного интервала нормально распределенной величины z при доверительной вероятности Рⁿ; t_p(n) — граница доверительного интервала случайной величины t, имеющей специальное распределение (таблицы этого распределения, по которым можно определитьV(n), имеются в литературе по теории вероятностей и математической статистике), зависящее от n, при доверительной вероятности Р. Если неравенства (14-15) и (14-16) не_; выполняются, то x_k следует считать промахом. Его необхо­димо исключить из ряда наблюдений, и для оценки результата измерения необходимо заново пересчитать 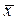и.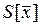

На практике часто встречается однократное измерение, когда измеряемая величина оценивается по результату одного наблю­дения. Этот случай можно рассматривать как частный случай многократных измерений (при n=1). Тогда выражения (14-13) и 14-14 примут вид:

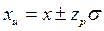; (14-17)

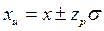. (14-18)

Здесь за действительное значение х измеряемой величины следует принять результат однократного измерения, из которого исключена систематическая погрешность. Нужно иметь в виду, что по однократному измерению нельзя определить s (или S). Поэтому для того чтобы можно было записать результат измере­ния в виде (14-17), среднее квадратическое отклонение s нужно знать на основании предварительных измерений или из техниче­ской документации на применяемое средство измерений. Если вместо σ известна его оценка S, найденная по некоторому числу предварительных измерений, то для определения t_p(f) в выраже­нии (14-18) число степеней свободы f нужно взять равным этому числу предварительных измерений минус единица.

Сравнение выражений (14-13), (14-14) и (14-17), (14-18) показывает, что увеличение числа наблюдений позволяет полу­чить более точную оценку истинного значения измеряемой вели­чины. Однако следует иметь в виду, что число наблюдений п не может быть сколь угодно большим, так как в течение длительного времени, необходимого для получения большого числа результа­тов наблюдений, нельзя гарантировать неизменность не только условий проведения эксперимента, но и размера самой измеряе­мой величины. Практически п следует ограничивать таким значе­нием, при котором случайная составляющая погрешности резуль­тата измерения будет существенно меньше не исключенных остат­ков систематических погрешностей отдельных результатов наблюдений.

Косвенные измерения. Допустим, что измеряемая величина у является функцией аргументов а, b, с,..., измеряемых прямыми измерениями, т.е. у = F(а, b, с,...). Проведя обработку ряда наблюдений для каждого аргумента методом, изложенным для прямых измерений, можно найти действительные значения аргументов

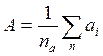
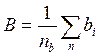
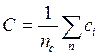
и оценки дисперсий A, B, C,...

; ; ….,

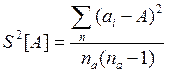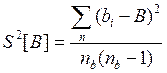где n _а, n_b, п_c,... — число измерений соответствующего аргумента.

Дальнейшую обработку результатов наблюдений можно про­водить по-разному. Наиболее распространенным является метод линеаризации, основанный на разложении функциональной зави­симости Y = F (A, B, C,...) в ряд Тейлора с ограничением ряда членами, содержащими только первые производные:

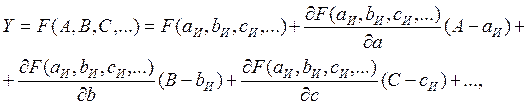(14-19)

где а_и, b_И, с_и,... — истинные значения аргументов.

Запишем выражение (14-19) в более компактной форме:

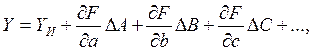(14-20)

где Y _и — истинное значение косвенно измеряемой величины; DA, DB, DC,... — погрешности результата измерения соответствующего аргумента;, 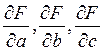… - значения частных производных от функции по соответствующему аргументу в точке, где аргументы имеют истинное значение. В правой части выражения (14-20) случайными величинами являются DA, DB, DC,... Если результаты измерения аргументов независимы друг от друга (что чаще всего и бывает на практике), то эти случайные величины являются независимыми.

Применяя к выражению (14-20) сформулированные выше правила, найдем математическое ожидание и дисперсию случай­ной величины Y, полученной при подстановке в функциональную зависимость значений аргументов A, B, C,...:

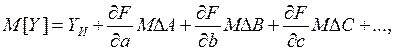(14-21)

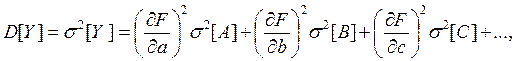(14-22)

где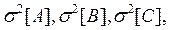...— дисперсии значений A, В, С,... аргументов.

Если при определении действительных значений аргументов A, В, С,... систематические погрешности были исключены, то М [DA] = М [DB] = М [DC] =... = 0. В этом случае М [Y] = Y_и и, следовательно, значение Y=F (А, В, С,...) можно принять за оценку действительного значения косвенно измеряемой величины. Что касается дисперсии полученного результата Y, то вычислить ее непосредственно по выражению (14-22) нельзя, так как для рас­чета значений частных производных требуется знание истинных значений аргументов. Вместо истинных значений аргументов известны их оценки A, В, С,.... Поэтому вместо значений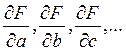

Нужно использовать их оценки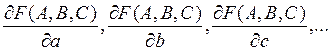вычисляя производные в точке, где аргументы принимают значения A, B, C, …

Если дисперсии аргументов известны, то оценка дисперсии результата измерения s² [Y] для косвенно измеряемой величины вычисляется по формуле

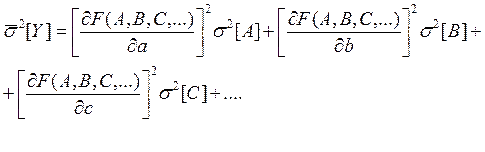(14-23)

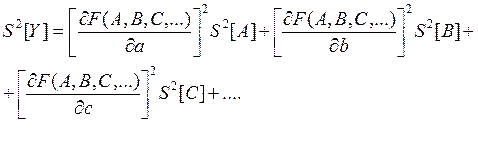
Для того чтобы найти доверительный интервал погрешности результата косвенного измерения, нужно определить закон рас­пределения величины 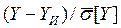или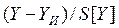

Закон распределения этих величин может быть весьма слож­ным даже при нормальном законе распределения случайных по­грешностей аргументов.

Если систематические погрешности при измерении аргумен­тов не исключаются, то результат измерения 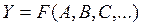косвенно измеряемой величины тоже

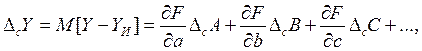(14-24)

содержит систематическую погрешность, равную математическому ожиданию погрешности 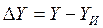На основании (14-21) эту погрешность можно представить в виде

где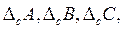...— систематическая погрешность результата измерения соответствующего аргумента. Заменяя значения част­ных производных, входящих в выражение (14-24), на значения этих производных в точке, где аргументы принимают значения A, В, С,..., получим выражение для оценки систематической погреш­ности результата косвенного измерения в виде

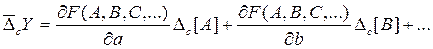(14-25)

При этом необходимо иметь в виду следующее. Очевидно, что оценить систематическую погрешность результата косвенного измерения по выражению (14-25) невозможно, не зная оценок систематических погрешностей измерения аргументов. Но если они известны, то их необходимо сразу исключить из результатов измерения аргументов и оценивать результат косвенного измере­ния по значениям аргументов, не содержащих систематических погрешностей. Поэтому выражением (14-25) следует пользовать­ся в том случае, когда систематические погрешности измерения аргументов не могли быть выявлены и оценены в процессе экспе­римента, а были оценены лишь после него. Это выражение может использоваться также при подготовке к эксперименту. Например, если предполагается, что погрешность результата косвенного измерения определяется только погрешностью средств измерений аргументов, причем у этих средств преобладающей является систематическая погрешность (случайной погрешностью можно пренебречь), то, пользуясь выражением (14-25), можно выбрать средства измерений с такими допустимыми предельными значе­ниями систематических погрешностей, чтобы погрешность ре­зультата измерения косвенно измеряемой величины не превысила заданного значения.

При однократных измерениях аргументов процедура опреде­ления результата косвенно измеряемой величины сохраняется такой же, как и при многократных измерениях, с учетом заме­чаний, сделанных при рассмотрении однократных прямых изме­рений.

Совместные измерения. Целью совместных измерений являет­ся установление функциональной зависимости между величина­ми, например зависимости сопротивления от температуры. Отыс­кивая зависимость между величинами а и b, необходимо устанавливать и измерять различные размеры величины а и одновре­менно измерять величину b. Таким образом, можно получить координаты исследуемой зависимости 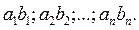Так как результаты измерения этих величин содержат погрешности, то полученные координаты не будут принадлежать истинной ис­следуемой зависимости. Исключив систематическую погрешность из каждого результата измерения, можно уточнить эти координа­ты, но и уточненные координаты все-таки будут отклоняться (рассеиваться) относительно истинной зависимости из-за слу­чайных погрешностей.

Степень рассеивания характеризуется дисперсией. Правиль­ной зависимостью, построенной по полученным координатным точкам, следует считать такую зависимость, при которой диспер­сия координатных точек относительно этой зависимости будет минимальной. Для оценки дисперсии нужно вычислить сумму квадратов отклонений координатных точек от истинной зависи­мости. Минимальной дисперсии будет соответствовать минималь­ное значение суммы квадратов этих отклонений. Поэтому метод, с помощью которого отыскивается истинная зависимость, назы­вается методом наименьших квадратов.

Рассмотрим применение этого метода на примере линейной зависимости между а и b. Предположим, нам известно, что зави­симость между а и b должна описываться уравнением

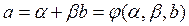(14-26)

Результаты эксперимента после исключения систематических погрешностей дают нам координаты исследуемой зависимости а₁, 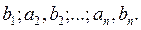Необходимо решить, как провести прямую линию, наилучшим образом согласующуюся с полученными ко­ординатами. Иными словами, зная координаты, полученные экс­периментально, и вид функции, нужно определить коэффици­енты 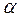и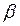

в уравнении (14-26).

В соответствии с уравнением (14-26), если b принимает зна­чение 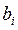то значение а должно быть равно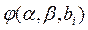, а экспери­мент дает значение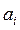. Следовательно, экспериментальная точка отклоняется от истинной точки на значение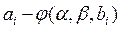. Сум­му квадратов отклонений экспериментальных точек от истинной зависимости можно найти по выражению

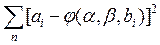(14-27)

где п — число экспериментальных точек.

Найдем значения коэффициенто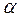и 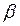в, обращающие выра­жение (14-

27) в минимум. Для этого продифференцируем это выражение по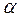и 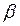и приравняем производные нулю:

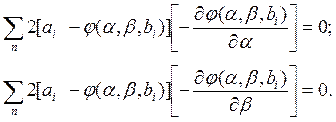(14-28)

Систему уравнений (14-28) с учетом (14-26) приведем к виду

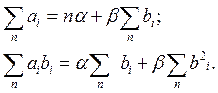(14-29)

Решая эту систему уравнений, получим выражение для коэффициента b:

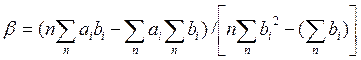(14-30)

а, зная β, находим выражение для a:

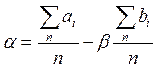(14-31)

Полученные значения a и b в общем случае отличаются от истинных значений коэффициентов уравнения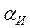и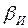

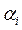
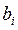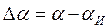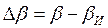и являются случайными величинами, так как координаты, искаженные случайными погрешностями, тоже являются случайными величи­нами. Погрешностями определения коэффициентов являются и Дисперсии этих погрешностей равны дисперсиям соответствующих коэффициентов, т. е. 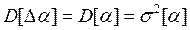и 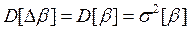Найдем эти дисперсии.

Сначала рассмотрим влияние погрешностей измерения а _i и b_i на рассеивание экспериментальных точек относительно исследуе­мой зависимости. Предположим, что мы хотим измерить величину а при b = b_i. Если измерения выполняются без погрешностей, то, установив значение b_i, получим значение величины а, соответ­ствующее координатной точке 1 (рис. 14-1), лежащей на исследуемой зависимости. Теперь допустим, что величина а изме­ряется без погрешности, а величина b с погрешностью. Тогда при установке значения b_i истинное значение величины b может ока­заться равным b_и за счет погрешности Db. Значение величины а при этом будет соответствовать координатной точке 2, лежащей на исследуемой зависимости. Однако, полагая, что мы установили значение b_i, вместо 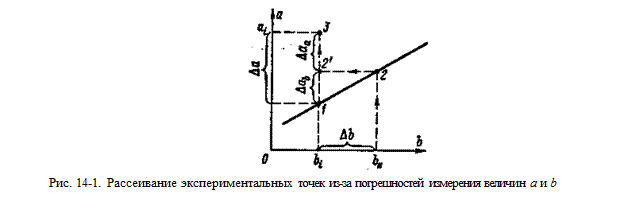координатной точки 2 мы будем рассматри­вать координатную точку 2', которая смещена с исследуемой зависимости на, 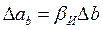где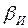— истинный коэффициент наклона иссле­дуемой зависимости. Если же и вели­чина а измеряется с погрешностью, то координатная точка 2' сместится на ве­личину этой погрешности D а _a и окажет­ся в точке 3. Именно эту точку мы и рассматриваем как точку с координатами а_i, b_i. Точка 3 смещена с исследуемой зависи­мости на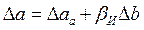. Очевидно, что экспериментальная точка 3 не изменит своего положения, если при изменении погреш­ностей D а_а и D b значение Dа будет оставаться неизменным. При этом значения коэффициентов b и a, рассчитанных по выраже­ниям (14-30) и (14-31), будут одни и те же, так как они определя­ются только положением экспериментальных точек. Поэтому мы можем считать, что измерение величины b осуществляется без погрешности, а рассеивание экспериментальных точек относи­тельно исследуемой зависимости обусловлено только погреш­ностью измерения величины а, причем эта погрешность 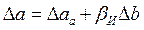. Погрешности D а_а и D b являются независимыми случайными величинами. Применяя правила нахождения диспер­сий, устанавливаем, что дисперсия, характеризующая рассеива­ние экспериментальных точек,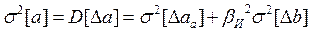

Считаем, что эта дисперсия одинакова при измерении любых значений а_i.

Перейдем теперь к непосредственной оценке дисперсий ко­эффициентов b и a. Считая, что величина b измеряется без по­грешности, мы имеем право рассматривать любые значения b_i, входящие в выражения для расчета коэффициентов, как неслу­чайные числа.

Выражение (14-30) путем алгебраических преобразований можно привести к виду

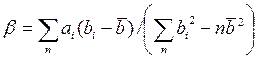
где 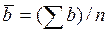- среднее арифметическое значение координат величины b.

Так как все а_i — независимые случайные величины с диспер­сией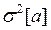, то дисперсию коэффициента b согласно ( 14-4) и (14-5) можно найти по выражению

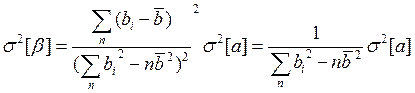(14-32)

Для нахождения дисперсии коэффициента, а удобнее вместо выражения (14-31) использовать выражение, которое можно получить, исключая из системы уравнений (14-29) коэффициент b и решая эту систему относительно коэффициента a:

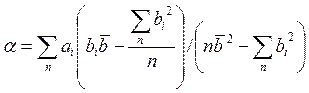
Отсюда находим дисперсию коэффициента α:

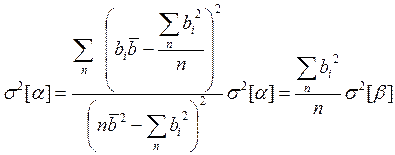(14-33)

Для расчета дисперсий по выражениям (14-32) и (14-33) необходимо знать дисперсию рассеивания экспериментальных точек 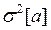. Точное значение этой дисперсии найти нельзя даже при известных дисперсиях погрешностей измерения величин а и b, так как еще необходимо знать истинный коэффициент наклона b_и. Поэтому вместо дисперси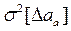й и 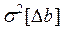получают их оценки 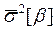и, и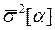спользуя вместо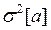одну из следующих ее оценок:

1) при известных дисперсиях погрешностей измерения

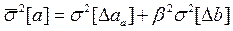
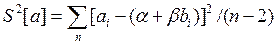
2) при известных оценках дисперсий погрешностей измерения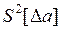 и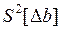

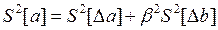
3) при отсутствии предварительной информации о дисперси­ях погрешностей или их оценках

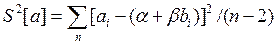
Последнее выражение является аналогом выражения (14-9). В числителе этих выражений стоят суммы квадратов отклонений отдельных результатов измерения от оценок их истинных значе­ний, в знаменателе — число степеней свободы. В математической статистике доказано, что при обработке совместных измерений число степеней свободы определяется числом координатных то­чек п минус число неизвестных коэффициентов т в исследуемой функциональной зависимости. В рассматриваемом случае т = 2 (коэффициенты a иb), поэтому число степеней свободы равно п — 2.

Совокупные измерения. Если число проведенных различных совокупных измерений равно числу измеряемых величин, то по результатам измерений можно составить систему уравнений, в которой число уравнений равно числу измеряемых величин. Решая систему уравнений, каждую измеряемую величину можно косвенно выразить через результаты совокупных измерений. Дальнейшую обработку можно проводить по правилам обработ­ки результатов наблюдений при косвенных измерениях. Если число различных совокупных измерений больше числа измеря­емых величин, то обработку результатов измерения проводят с помощью метода наименьших квадратов.