Суммирование погрешностей

В практике измерений часто встает задача определения ре­зультирующей (суммарной) погрешности по известным значени­ям составляющих этой погрешности.

При рассмотрении составляющих погрешности как случай­ных величин, результирующую погрешность следует определять по правилу суммирования случайных величин. Это правило осно­вано на известных из теории вероятностей положениях:

1) математическое ожидание (систематическая погрешность) результирующей погрешности определяется алгебраической суммой математических ожиданий (систематических погрешностей) составляющих (14-1);

2) дисперсия результирующей погрешности определяется согласно (14-4) выражением

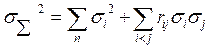(14-34)

где 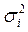— дисперсия i-и составляющей погрешности; п — число суммируемых составляющих погрешностей; r_ij— коэффициент корреляции между i- и j-и составляющими, знак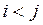под суммой означает, что суммирование распространяется на все возможные попарные сочетания составляющих погрешностей, для которых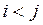

Нахождение результирующей систематической погрешности по известным систематическим погрешностям суммируемых со­ставляющих не вызывает трудностей. Использование же выраже­ния (14-34) для расчета 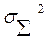затруднительно, так как точное значе­ние коэффициента корреляции между составляющими обычно неизвестно. В этом случае при расчетах полагают r равным нулю, если случайные составляющие можно считать независимыми, или равным единице со знаком плюс или минус, если заметна корре­ляция между суммируемыми случайными составляющими по­грешностей. Рассмотрим подробнее суммирование случайных по­грешностей.

Суммирование случайных погрешностей при нормальных за­конах их распределения. Будем считать, что результирующая погрешность измерения состоит из п случайных составляющих, имеющих нормальный закон распределения; ±s_im — границы доверительного интервала i-й случайной составляющей.

Зная доверительную вероятность и доверительный интервал для каждой составляющей погрешности, можно найти среднее квадратическое отклонение каждой из них по формуле

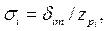(14-35)

где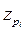— коэффициент, взятый из таблиц для нормального рас­пределения и соответствующий доверительной вероятности P_i. Если доверительная вероятность для всех составляющих оди­накова и равна Р, то, используя выражения (14-34) и (14-35), получаем:

а) для коррелированных составляющих (r _ij равен + 1 или - 1)

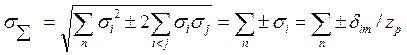(14-36)

где знак «±» означает, что для составляющих с положительной корреляцией s_i и s_im нужно брать со знаком «+», а для составля­ющих с отрицательной корреляцией — со знаком «—»;

б) для независимых составляющих (r_ij = 0)

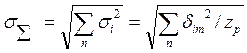(14-37)

При суммировании составляющих, имеющих нормальный за­кон распределения, результирующая погрешность будет иметь тоже нормальный закон распределения. Поэтому границы дове­рительного интервала результирующей погрешности с довери­тельной вероятностью Р

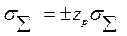(14-38)

С учетом (14-36) и (14-37) выражение (14-38) принима­ет вид

а) для коррелированных составляющих

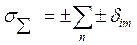(14-39)

б) для независимых составляющих

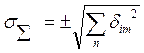(14-40)

Если в выражении (14-39) все составляющие имеют положи­тельную корреляцию, то

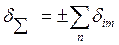(14-41)

Суммирование погрешностей по выражению (14-41) назы­вается арифметическим суммированием, а по выражению (14-40) — геометрическим суммированием.

Действительные значения коэффициентов корреляции по аб­солютному значению могут находиться в пределах от нуля до единицы, поэтому арифметическое суммирование обычно дает завышенное значение суммарной погрешности.

Если для суммируемых составляющих погрешностей извест­ны их предельные значения, то предельное значение результиру­ющей погрешности находят путем арифметического суммирова­ния предельных значений составляющих.

Суммирование случайных погрешностей при их законах рас­пределения, отличных от нормального. Трудность нахождения суммарной погрешности в этом случае заключается в том, что закон ее распределения зависит от конкретных видов и характе­ристик законов распределения суммируемых составляющих. На­пример, при сложении двух независимых случайных погрешно­стей, имеющих равномерные законы распределения с одинаковыми дисперсиями, результирующая погрешность будет распределяться по треугольному закону. Если же эти равномерные законы имеют разные дисперсии, то результирующая погреш­ность будет распределяться по трапецеидальному закону. Поэто­му для установления доверительного интервала результирующей погрешности необходимо в каждом конкретном случае искать методами теории вероятностей закон распределения результиру­ющей погрешности.

Зная закон распределения результирующей погрешности, можно найти доверительный интервал этой погрешности по выра­жению, аналогичному (14-38):

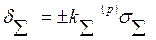
где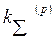— коэффициент, зависящий от закона распределения ре­зультирующей погрешности и доверительной вероятности Р.

Возможны приближенные способы определения доверитель­ного интервала суммарной погрешности без установления закона распределения результирующей погрешности.

Первый способ базируется на центральной предельной теоре­ме: если число суммируемых независимых составляющих доста­точно велико (практически при 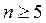среди этих составляющих не должно быть существенно преоблада­ющих над остальными.), то закон распределения результирующей погрешности близок к нормальному и в качестве коэффициента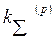можно принимать z_p.

Второй способ основан на исследовании (Петров В. П., Рясный Ю. В. Оценка суммарной погрешности средств измерений//Измерительная техника.— 1977.— № 2.), показавшем, что при суммировании независимых составляющих, имеющих законы распределения, изложенные в ГОСТ 8.011—72, можно пользоваться приближенными значениями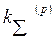: при доверительной вероятности Р = 0,90 коэффициент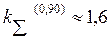, а при доверительной вероятности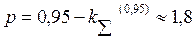. При этом погрешность в определении 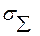не превышает ±10%.