Исходные данные:
Для схем, изображенных на рис. 5.1, требуется рассчитать мгновенные значения величины (или всех токов и напряжений), указанной в таблице 6.1, после выполнения коммутации. Выбор схемы, параметров ее элементов и вида коммутации осуществляются с помощью табл. 5. 1, в соответствии с вариантом задания. Расчет выполнить классическим и операторным методами.
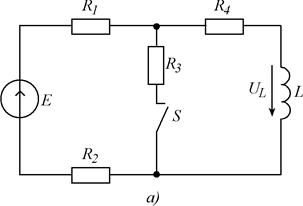
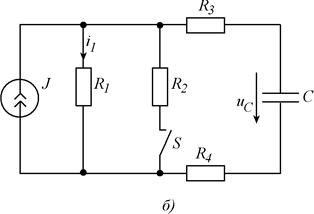
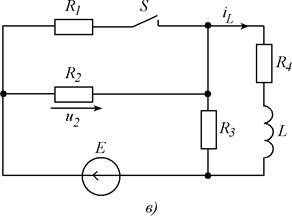
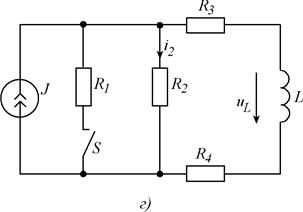
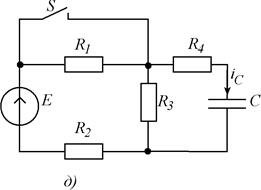
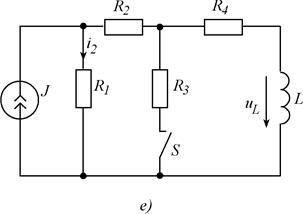
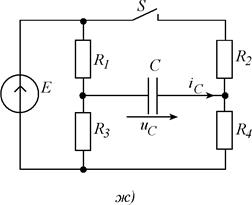
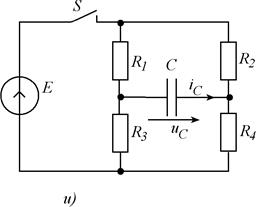
Рис. 5.1. Схемы заданий.

 ;
; 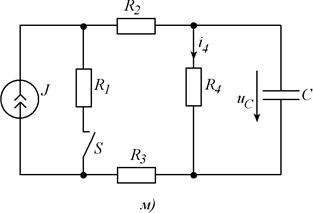
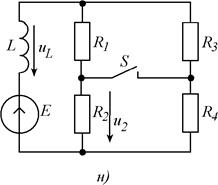
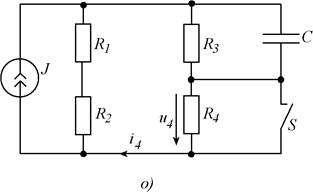
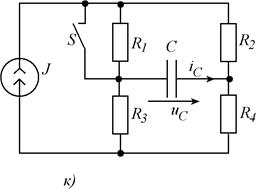
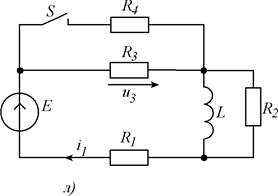
Рис. 5.1 (продолжение). Схемы заданий к заданию.
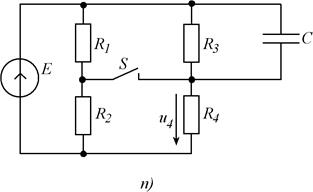
Рис. 5.1(продолжение). Схемы заданий к заданию.
Таблица 5.1
Параметры элементов схемы
| Вари ант | Схема | Е,В | J,A | L, мГн | С. мкФ | R 1 Ом | R 2 Ом | R 3 Ом | R 4 Ом | Найти | Ключ S |
| а | - | - | uL | ||||||||
| б | - | - | uС | Р | |||||||
| в | - | - | iL | ||||||||
| г | - | - | I2 | р | |||||||
| д | - | - | iС | ||||||||
| е | - | - | uL | Р | |||||||
| ж | - | - | uС | ||||||||
| 3 | - | - | uL | р | |||||||
| и | - | - | iС | ||||||||
| и | - | - | uС | р | |||||||
| л | - | ~ | U3 | ||||||||
| м | - | - | I4 | р | |||||||
| н | - | - | uL | ||||||||
| о | - | - | I1 | р | |||||||
| п | - | - | U4 | ||||||||
| р | - | - | I4 | р | |||||||
| а | - | - | I1 | р | |||||||
| б | - | - | I1 | ||||||||
| в | - | - | U2 | р | |||||||
| г | - | - | uL | ||||||||
| д | - | - | I3 | р | |||||||
| е | - | - | uL | ||||||||
| ж | - | - | iС | р | |||||||
| 3 | - | - | iL | ||||||||
| и | - | - | uС | р | |||||||
| к | - | - | iС | ||||||||
| л | - | - | I1 | р | |||||||
| м | - | - | uС | ||||||||
| н | - | - | U2 | р | |||||||
| о | - | - | U4 |
Примечание: Р — ключ S размыкается; 3 — ключ S замыкается.
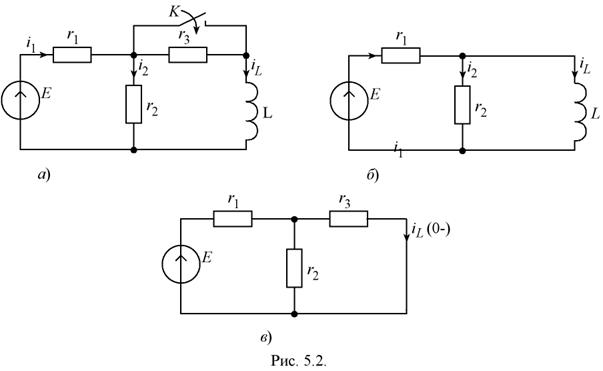
В электрической цепи, схема которой приведена на рис. 5.2, а, замыкается ключ К Требуется определить ток в индуктивности L и построить его зависимость от времени t, если параметры элементов цепи имеют следующие значения: Е = 30 В; r 1 = r 2 = r 2 = 10 Ом; L = 0,1 Гн.
1. Классический метод. Рассматривая схему цепи, приведенную на рис. 5.2 а, можно сделать следующие выводы:
1) в схеме имеется один реактивный элемент L, поэтому дифференциальное уравнение цепи будет иметь первый порядок;
2) при коммутации цепи сопротивление r 3 замыкается ключом К, поэтому в дальнейшем переходном процессе не участвует;
3) переходный процесс связан с изменением энергии, запасенной в индуктивности L, при изменении структуры цепи, обусловленной замыканием сопротивления r 3.
Составим систему уравнений цепи по законам Кирхгофа, для схемы, полученной после коммутации (рис. 5.2, б):
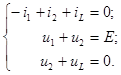
После подстановки напряжений эти уравнения приводятся к виду:
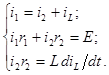
Выполнив взаимные подстановки, получим дифференциальное уравнение для тока в индуктивности
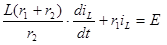
После подстановки в это уравнение значений параметров элементов, получим:
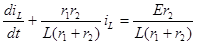 или
или 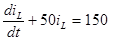
Решение этого неоднородного дифференциального уравнения состоит из двух частей:
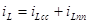
где принужденная составляющая тока определяется в установившемся режиме после коммутации и равна (рис. 5.2 б):
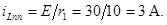
Для определения свободной составляющей тока 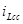 положим правую часть дифференциального уравнения равной нулю, тогда получим:
положим правую часть дифференциального уравнения равной нулю, тогда получим:
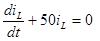 .
.
Решение этого уравнения имеет вид:
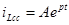
Характеристическое уравнение, соответствующее дифференциальному уравнению для свободной составляющей тока, имеет вид: р + 50 = 0, откуда находим р = -50 с-1. Модуль этой величины характеризует скорость уменьшения свободной составляющей тока и называется коэффициентом затухания. Величина, обратная коэффициенту затухания, имеет размерность времени и называется постоянной времени цепи
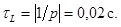
Таким образом, полный ток в индуктивности можно записать в виде:
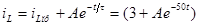
При определении постоянной интегрирования А воспользуемся первым законом коммутации, согласно которому 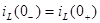 Для вычисления тока
Для вычисления тока 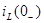 построим схему, изображенную на рис. 5.3 в. На этой схеме индуктивность L заменена перемычкой, поэтому ток в ней рассчитаем по методу эквивалентного источника, преобразуя ветви с источником напряжения Е и сопротивлениями
построим схему, изображенную на рис. 5.3 в. На этой схеме индуктивность L заменена перемычкой, поэтому ток в ней рассчитаем по методу эквивалентного источника, преобразуя ветви с источником напряжения Е и сопротивлениями 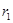 ,
, 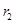 , к эквивалентному источнику с параметрами:
, к эквивалентному источнику с параметрами:
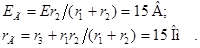
Ток в индуктивности до коммутации (т. е. при t = 0-) определяется по формуле:
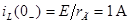
Подставив найденное значение тока  в уравнение для полного тока в индуктивности, получим:
в уравнение для полного тока в индуктивности, получим:
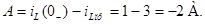
Окончательное решение для тока в индуктивности представим в виде:
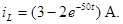
График тока в индуктивности приведен на рис. 5.3. При 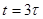 значение тока
значение тока 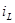 отличается от принужденного всего на 5%. Поэтому принято считать, что переходный процесс практически заканчивается через интервал времени
отличается от принужденного всего на 5%. Поэтому принято считать, что переходный процесс практически заканчивается через интервал времени 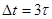 . Из графика видно, что ток в индуктивности монотонно изменяется от начального значения 4(0) до конечного значения, равного iLпр = 3 А.
. Из графика видно, что ток в индуктивности монотонно изменяется от начального значения 4(0) до конечного значения, равного iLпр = 3 А.
Располагая током в индуктивности, найдем напряжения и токи в других ветвях.
Напряжение на индуктивности определим по формуле:
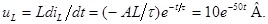
График напряжения на индуктивности приведен на рис. 5.3. Из этого графика видно, что напряжение на индуктивности в результате коммутации скачком изменяется от начального значения 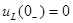 до значения
до значения 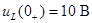 . После этого оно монотонно убывает до значения
. После этого оно монотонно убывает до значения 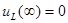 .
.
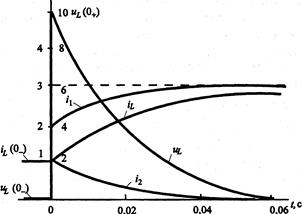
Рис. 5.3. Графики напряжения и токов в цепи.
Токи в сопртивлениях определяем по формулам:
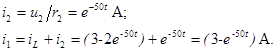
Графики токов в сопротивлениях  и
и  также представлены на рис. 5.3.
также представлены на рис. 5.3.
2 .Операторный метод. В основу операторного метода расчета переходных процессов положено интегральное преобразование Лапласа:
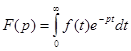 ,
,
где 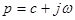 ‑ комплексная переменная, обычно называемая оператором,
‑ комплексная переменная, обычно называемая оператором, 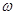 ‑ угловая частота, с – некоторая вещественная постоянная. Применительно электрическим цепям оператор p можно рассматривать как комплексную частоту
‑ угловая частота, с – некоторая вещественная постоянная. Применительно электрическим цепям оператор p можно рассматривать как комплексную частоту 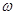 , в которой c >0 характеризует затухание гармонических колебаний, представленных вращающимся вектором
, в которой c >0 характеризует затухание гармонических колебаний, представленных вращающимся вектором 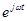 .
.
Алгоритм расчета цепей операторным методом состоит из трех основных этапов:
- составления операторной схемы замещения цепи;
- расчета операторной схемы замещения;
- определения оригинала реакции цепи по его операторному изображению.
Для составления операторной схемы замещения, произвести замену элементов оригинальной схемы их операторными эквивалентами, используя таблицу соответствия (табл. 5.2).
Табл. 5.2
| Элемент цепи | Оригинальная схема | Операторная схема |
| Источник напряжения | 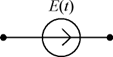 | 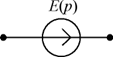 |
| Источник тока | 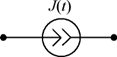 | 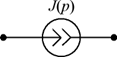 |
| Сопротивление |  |  |
| Индуктивность | 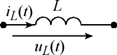 | 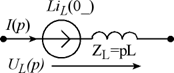 |
| Емкость | 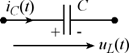 | 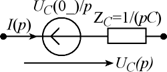 |
Построим операторную схему замещения которая соответствует оригинальной схеме после замыкания ключа К (см. рис. 5.2.)
На основании законов Кирхгофа составим уравнения для полученной схемы.
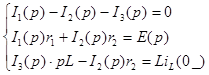
Решая системы уравнений определяем операторные токи и операторные напряжения. Располагая операторными значениями токов и напряжений, определяем их оригинальные (мгновенные) значения.
Задание 6. РАCЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ ВТОРОГО ПОРЯДКА
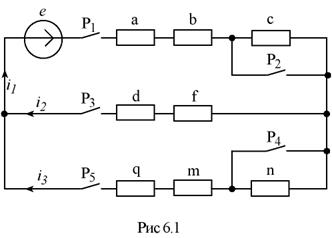 |
Исходные данные:
В цепи изображенной на рис. 6.1, происходит коммутация в момент времени t=0 ЭДС источника Е = const. Величина ЭДС задается преподавателем. Параметры схемы и характер переключения ключей для каждого варианта заданы в табл. 6.1. Прочерки в столбцах a, b, c, d. f, q, m, n означает отсутствие элемента. Прочерк в столбцах Р1 - Р5 соответствует замкнутому положению ключа. Буква «З» означает операцию замыкания, буква «Р» - операцию размыкания соответствующего ключа.
В таблице элемент, сопротивление которого задано в Ом, является резистором R.
Требуется:
1. Найти законы изменения токов i 1, i 2, i 3 и напряжений на емкости (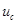 ) и индуктивности (
) и индуктивности (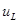 ). Задачу решить классическим и операторным методами.
). Задачу решить классическим и операторным методами.
2. Построить временные диаграммы токов i 1, i 2, i 3 и напряжений 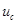 и
и 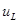 .
.
3. Составить математическую модель переходного процесса по методу переменных состояния и подготовить систему дифференциальных уравнений. Полученные уравнения решить с помощью прикладных программ на компьютере (MathCАD, MathLab и др).
4. Сравнить результаты расчета полученные различными методами.
Рассмотрим различные способы расчета переходных процессов.
I. Классический метод.
1. При расчете переходного процесса классическим методом составляют систему интегро-дифференциальных уравнений цепи, используя для этого законы Кирхгофа и уравнения связи, являющиеся уравнениями отдельных элементов:
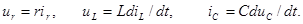
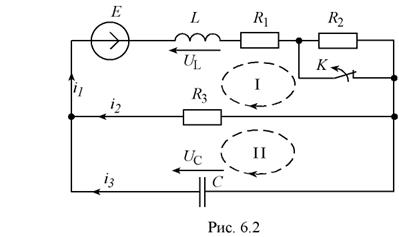
Для примера рассмотрим вариант №30, схема которого составлена с учетом таблицы 6.1 и изображена на рис. 6.2 (E=104 В, R1=20 Ом, R2=100 Ом, R1=500 Ом, L=0,02 Гн, С=0,5 мкФ).
I.1. В начале выбираем условно - положительные направления токов в ветвях и направления обхода контуров. На основании законов Кирхгофа составим систему уравнений.
| Таблица 6.1 | |||||||||||||
| Вариант | Условия | ||||||||||||
| Элементы схемы | Положение ключей | ||||||||||||
| a | b | c | D | f | q | m | N | P1 | P2 | P3 | P4 | P5 | |
| 0,5 Гн | 600 Ом | ‑ | 103 Ом | ‑ | 10 мкФ | ‑ | ‑ | з | ‑ | ‑ | ‑ | ‑ | |
| 0,3 Гн | 120 Ом | - | 500 Омч | ‑ | 8мкФ | _- | - | - | - | з | - | - | |
| 0.1 Гн | 350 Ом | - | 600 Ом | ‑ | 6мкФ | - | - | - | - | - | - | з | |
| 0,08 Гн | 40 Ом | 160 Ом | 200 Ом | ‑ | 4мкФ | - | - | - | з | - | - | - | |
| 0,03 Гн | 500 Ом | - | 0,8мкФ | ‑ | 800 Ом | - | 700 Ом | - | - | - | з | - | |
| 0,03 Гн | - | 100 Ом | 500 Ом | ‑ | 0,5мкФ | - | - | - | р | - | - | - | |
| 0,09 Гн | 300 Ом | - | 5 мкФ | - | 300 Ом | - | 600 Ом | - | - | - | р | - | |
| 9 мкФ | 500 Ом | - | 700 Ом | - | 0,4 Гн | - | - | з | - | - | - | - | |
| 0,6мкФ | - | - | 600 Ом | - | 0,01 Гн | 450 Ом | - | з | - | - | - | - | |
| 300 Ом | - | - | 2 мкФ 0,7мкФ | - | 0,06 Гн | 70 Ом | - | з | - | - | - | - | |
| 700 Ом | - | - | 0,7мкФ | - | 0,02 Гн | 400 Ом 80 | - | - | - | з | - | - | |
| 400 Ом | - | - | 0,9мкФ | 0,04 Гн | 80 Ом | - | - | - | - | - | з | ||
| 600 Ом | - | 300 Ом | 0,6мкФ | - | 0,01 Гн | 300 Ом | - | - | з | - | - | - | |
| 500 Ом | - | - | 1 мкФ | - | 0,05 Гн | 140 Ом | 360 Ом | - | - | - | з | - | |
| 250 Ом | - | 250 Ом | 8 мкФ | - | 0,3 Гн | 100 Ом | - | - | р | - | - | - | |
| 103 Ом | - | - | 10мкФ | - | 0,5Гн | 200 Ом | 500 Ом | - | - | - | р | - | |
| 0,09 Гн | - | - | 900 Ом | - | 5 мкФ | 350 Ом | - | з | - | - | - | - | |
| 0,09 Гн | - | - | 200 Ом | - | 4 мкФ | 30 Ом | - | - | - | з | - | - | |
| 0,03 Гн | - | - | 800 Ом | - | 0,8мкФ | 650 Ом | - | - | - | - | - | з | |
| 0,02 Гн | - | 800 Ом - | 700 Ом | - | 0,7мкФ | 550 Ом | - | - | з | - | - | - | |
| 0,07 Гн | - | - | 3 мкФ | 80 Ом | 400 Ом | - | 600 Ом | - | - | - | з | - | |
| 0,2Гн | - | - | 7 мкФ | 400 Ом | 200 Ом | - | 600 Ом | - | - | - | р | - | |
| 500 Ом | - | - | 0,02 Гн | - | 100 Ом 750 Ом | 0,5мкФ | - | з | - | - | - | - | |
| 700 Ом | - | - | 0,4 Гн | - | 750 Ом | 9 мкФ | - | - | - | з | - | - | |
| 300 Ом | - | 250 Ом - | 0,06 Гн | - | 50 Ом | 2 мкФ | - | - | з | - | - | - | |
| 400 Ом | - | 400 Ом | 0,2 Гн | - | 500 Ом | 7 мкФ | - | - | р | - | - | - | |
| 400 Ом | - | - | 0,9мкФ | 100 Ом | 0,04Гн | - | 400 Ом | - | - | - | з | - | |
| 2 мкФ | - | 2 мкФ | 500 Ом | - | 0,05Гн | 120 Ом | - | - | з | - | - | - | |
| 6 мкФ | - | 3 мкФ | 600 Ом | - | 0,1Гн | 400 Ом | - | - | з | - | - | - | |
| 0,02Гн | 20 Ом | 100 Ом | 500 Ом | - | 0,5мкФ | - | - | - | р | - | - | - |
 |
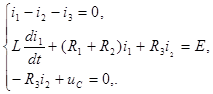 (6.1)
(6.1) и уравнение связи 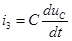
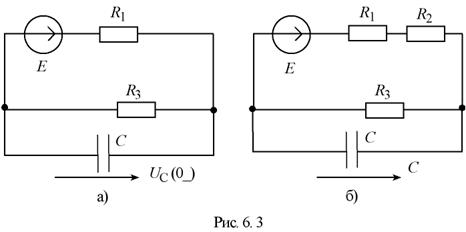
1.2. Определение независимых и зависимых начальных значений, напряжений и токов в схеме в момент времени 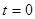 (Рис. 6.3,а):
(Рис. 6.3,а):
I.2.1 Независимые начальные условия определяются количеством реактивных накопителей энергии в схеме. Состояние каждого накопителя может быть охарактеризовано либо текущим через него током, либо падением напряжения на нем. Независимыми переменными являются: для емкости – напряжение на ней, для индуктивности – ток через нее.
Согласно первому закону коммутации ток через индуктивность непосредственно до коммутации 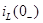 равен току через ту же индуктивность после коммутации
равен току через ту же индуктивность после коммутации 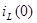 . Ток через индуктивность L (рис. 6.3, а) до коммутации имел значение:
. Ток через индуктивность L (рис. 6.3, а) до коммутации имел значение:
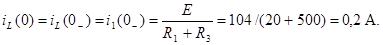 (6.2)
(6.2)
Ток в емкости до коммутации отсутствовал, поэтому 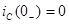 .
.
Напряжение на индуктивности также отсутствовало, поэтому 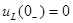 .
.
Согласно второму закону коммутации, напряжение на емкости до коммутации равно напряжению непосредственно после коммутации. Напряжение до коммутации было равно падению напряжения на резисторе R3, включенным параллельно ей:
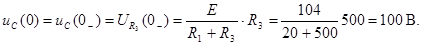 (6.3)
(6.3)
I.2.2. Зависимые начальные условия. Значения остальных токов и напряжений при 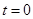 в послекоммутационной схеме (рис 6.2), определяемые по независимым начальным значениям из законов Кирхгофа называются зависимыми начальными условиями. Составим систему уравнений для определения зависимых начальных условий:
в послекоммутационной схеме (рис 6.2), определяемые по независимым начальным значениям из законов Кирхгофа называются зависимыми начальными условиями. Составим систему уравнений для определения зависимых начальных условий:
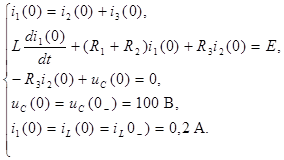 (6.4)
(6.4)
Подставляя данные схемы, получаем:
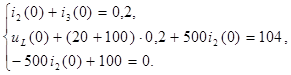 (6.5)
(6.5)
Решая систему уравнений (6.5) находим зависимые начальные условия:
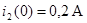 ;
; 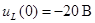 ;
; 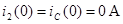 . (6.6)
. (6.6)
I.3. Система уравнений (6.1) сводится к одному дифференциальному уравнению второго порядка относительно напряжения 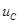 . (Если систему уравнений (6.1) сводить к одному уравнению относительно тока
. (Если систему уравнений (6.1) сводить к одному уравнению относительно тока 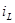 , то получиться не дифференциальное уравнения, а интегро-дифференциальное уравнение). Для этого из третьего и первого уравнений системы (6.1):
, то получиться не дифференциальное уравнения, а интегро-дифференциальное уравнение). Для этого из третьего и первого уравнений системы (6.1):
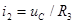 , (6.7)
, (6.7)
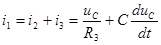 . (6.8)
. (6.8)
Дифференцируя (6.7) и подставляя результат во второе уравнение системы (6.1), получим
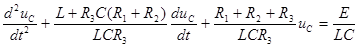 . (6.9)
. (6.9)
Получено линейное неоднородное дифференциальное уравнение второго порядка. Известно, что решением таких уравнений является сумма двух составляющих, а именно, общего решения для соответствующего однородного уравнения и частного решения, полученного в форме правой части для неоднородного уравнения. Физический смысл первой составляющей – описание поведения системы при отсутствии внешнего воздействия. Эту составляющую принято называть свободной составляющей (далее обозначено 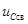 ). Физический смысл второй составляющей – описание поведения системы при наличии внешнего воздействия, описываемого правой частью неоднородного уравнения. Эту составляющую принято называть принужденной составляющей (далее обозначена u Cпр). По существу, это описание нового установившегося процесса, в которой должна будет перейти система после коммутации.
). Физический смысл второй составляющей – описание поведения системы при наличии внешнего воздействия, описываемого правой частью неоднородного уравнения. Эту составляющую принято называть принужденной составляющей (далее обозначена u Cпр). По существу, это описание нового установившегося процесса, в которой должна будет перейти система после коммутации.
Таким образом, решение уравнения (6.9)
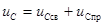 . (6.10)
. (6.10)
Принужденная составляющая напряжения u C определяется в установившемся режиме после коммутации и равна (рис.6.3, б)
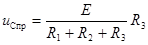 . (6.11)
. (6.11)
Свободная составляющая напряжения 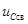 определяется решением однородного дифференциального уравнения
определяется решением однородного дифференциального уравнения
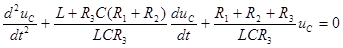 . (6.12)
. (6.12)
Решение однородного дифференциального уравнения (6.12) позволяет найти свободную составляющую напряжения
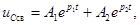 (6.13)
(6.13)
где 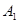
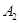 ‑ постоянные интегрирования, определяются из начальных условий, отражающих сохранение начальных запасов энергии в емкости
‑ постоянные интегрирования, определяются из начальных условий, отражающих сохранение начальных запасов энергии в емкости 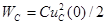 и катушке индуктивности
и катушке индуктивности 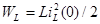 ;
;
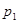 и
и 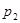 определяются как корни характеристического уравнения, соответствующего дифференциальному уравнению (6.12)
определяются как корни характеристического уравнения, соответствующего дифференциальному уравнению (6.12)
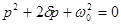 , (6.13)
, (6.13)
где 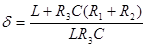 ‑ коэффициент затухания колебаний в контуре;
‑ коэффициент затухания колебаний в контуре; 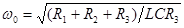 ‑ угловая частота незатухающих колебаний.
‑ угловая частота незатухающих колебаний.
Решением характеристического уравнения (6.13) являются корни:
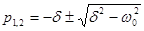 . (6.14)
. (6.14)
По их виду можно судить о характере переходного процесса:
‑Если 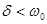 корни получаются комплексными, сопряженными с отрицательной вещественной частью
корни получаются комплексными, сопряженными с отрицательной вещественной частью 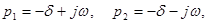 где
где 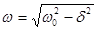 . Тогда переходный процесс носит колебательный характер, и полное решение уравнения (6.9) принимает вид
. Тогда переходный процесс носит колебательный характер, и полное решение уравнения (6.9) принимает вид

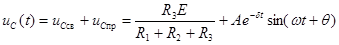 . (6.15)
. (6.15)
Скорость изменения напряжения на конденсаторе
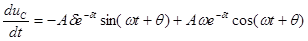 . (6.16)
. (6.16)
Если корни характеристического уравнения отрицательные, вещественные и разные, переходный процесс носит затухающий апериодический характер. Полное решение дифференциального уравнения (6.9) для емкости имеет вид:
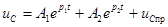 . (6.17)
. (6.17)
Скорость изменения напряжения на конденсаторе
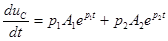 . (6.18)
. (6.18)
Поскольку (для нашего варианта) корни характеристического уравнения (6.13) являются комплексными (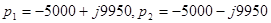 ), то свободная составляющая решения имеет характер затухающих во времени колебаний.
), то свободная составляющая решения имеет характер затухающих во времени колебаний.
I.4. Определение постоянных интегрирования. Постоянные интегрирования (А1, А 2) в зависят от параметров цепи, ЭДС и момента включения (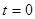 ). Постоянные могут быть определены посредством решения алгебраических уравнений (6.17) и (6.18) с учетом начальных условий. Поэтому подставим в оба выражения
). Постоянные могут быть определены посредством решения алгебраических уравнений (6.17) и (6.18) с учетом начальных условий. Поэтому подставим в оба выражения 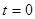 . Числовые значения левой части уравнений определены в начальных условиях (см. выше, п. I.2). В результате, получаем систему алгебраических уравнений:
. Числовые значения левой части уравнений определены в начальных условиях (см. выше, п. I.2). В результате, получаем систему алгебраических уравнений:
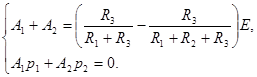 (6.19)
(6.19)
Решение системы уравнений позволяет найти постоянные интегрирования А 1 и А 2.
В случае, когда корни характеристического уравнения комплексно сопряженные, воспользуемся уравнениями (6.15) и (6.16). Тогда система уравнений для определения постоянных интегрирования принимает вид
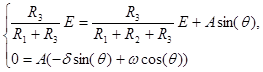 (6.20)
(6.20)
где 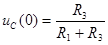 и
и 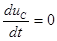 определены в начальных условиях п.I.2. Решая систему уравнений (6.20), определяем
определены в начальных условиях п.I.2. Решая систему уравнений (6.20), определяем 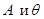 .
.
После подстановки постоянных интегрирования в формулу (6.15) (или (6.17)), получаем окончательное значение напряжения на емкости. Полученные значения проверяем задавая 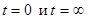 .
.
Для варианта 30: 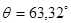 ,
, 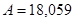 В.
В.
Окончательное значение напряжения на емкости:
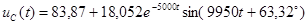 .
.
График напряжения 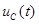 приведен на рис. 6.4.
приведен на рис. 6.4.
Остальные токи и напряжения определяются с помощью системы уравнений (6.1).
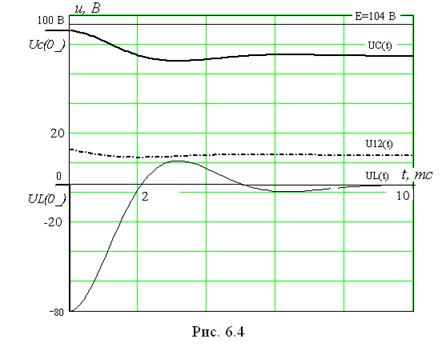
Зависимости токов от времени приведены на рис. 6.5.
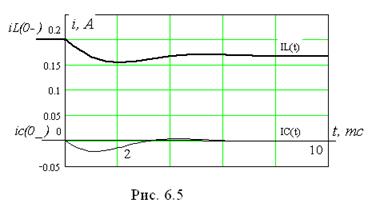
При апериодическом процессе (корни характеристического уравнения вещественные) диаграммы строятся для промежутка времени 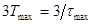 (
(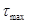 - набольшая постоянная времени, получающаяся при расчете). При колебательном процессе (корни характеристического уравнения комплексные) этот промежуток составляет
- набольшая постоянная времени, получающаяся при расчете). При колебательном процессе (корни характеристического уравнения комплексные) этот промежуток составляет 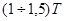 (
(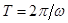 ‑период колебаний).
‑период колебаний).
В указанных промежутках должно быть рассчитано не менее десяти точек для апериодического процесса и не менее пятнадцати точек для колебательного процесса. Шкалы на графиках должны быть оформлены по ГОСТ.
II. Расчет переходного процесса операторным методом
Расчет переходного процесса операторным методом производится в следующей последовательности.
II.1. Строится операторная схема замещения. Для этого необходимо:
- мгновенные значения токов, напряжений и ЭДС заменить их изображениями по Лапласу;
- индуктивность заменить последовательным соединением операторного сопротивления pL и добавочного источника, ЭДС которого совпадает по направлению с током 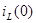 и равна
и равна 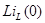 ;
;
- емкость заменить последовательным соединением операторного сопротивления 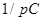 и добавочного источника, ЭДС которого направлена противоположно напряжению
и добавочного источника, ЭДС которого направлена противоположно напряжению 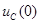 и равна
и равна 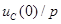 .
.
Для рассматриваемой цепи операторная схема изображена на рис. 6.6.
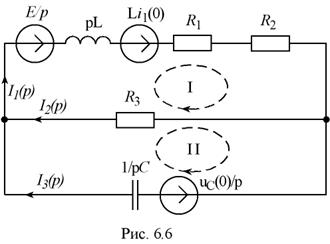
II.2. Для полученной операторной схемы замещения составляется система уравнений, по первому и второму законам Кирхгофа в операторной форме.
Для рассматриваемого примера эта система уравнений имеет вид
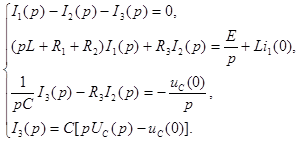
II.3. Преобразованная по Лапласу система уравнений решается относительно изображения искомой переменной (в рассмотренном случае относительно 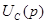 ). Решение должно быть представлено в виде отношения двух полиномов оператора p.
). Решение должно быть представлено в виде отношения двух полиномов оператора p.
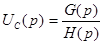 .
.
При этом необходимо преобразовывать, чтобы в составе Н(р) множитель при р в наивысшей степени был бы равен единице, как это требуется при разложении дроби на простейшие.
II.4. По теореме разложения находится оригинал-закон изменения искомой переменной (в рассмотренном примере uC(t)). В простейших случаях оригинал можно находить по формулам соответствия f(t):=:F(p).
III Расчет, переходных процессов по методу переменных состояния.
В основу метода переменных состояния положена принципиальная возможность замены дифференциального уравнения n –го порядка электрической цепи системой из n дифференциальных уравнений первого порядка. При этом, в качестве переменных состояния, принимают токи в индуктивности i L и напряжение u C на емкостях, которые однозначно определяют запас энергии в любой момент времени. Переходный процесс в рассматриваемой цепи описывается системой дифференциальных уравнений в форме Коши и системой начальных условий.
Из системы уравнений 5.1 получаем
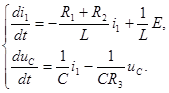
Подставим численные значения величин параметров цепи
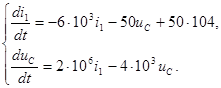 (6.16)
(6.16)
Находим начальные условия
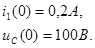 (6.17)
(6.17)
Систему уравнений (6.16) необходимо решить численными методами. При численном способе решения уравнений состояния используют различные программы численного интегрирования на ЭВМ: метод Рунге-Кутта, метод Эйлера, метод трапеций и др. Так, например, в пакете программ MathCAD 2000 [5] приведены программы численного решения дифференциальных уравнений модифицированном методом Эйлера и методом Рунге-Кутта. Поскольку погрешность решения методом Эйлера достигает нескольких процентов, то более предпочтительным является метод Рунге-Кутта, который при решении уравнений четвертого порядка дает погрешность h-4, где h — шаг приращения переменной. Этот метод обеспечивает контроль точности вычислений на каждом шаге интегрирования и программную регулировку шага.
Систему уравнений (6.16) и начальные условия (6.17) запишем в матричном виде.
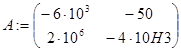 ,
, 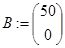 ,
, 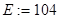 ,
, 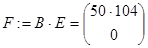 ,
, 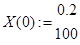 ,
,
где А ‑ собственные коэффициенты системы; В – вектор коэффициентов при воздействиях; X(0) ‑ вектор начальных условий; F – величина входных воздействий.
В системе MathCAD программа интегрирования уравнений по методу Рунге-Кутта имеет имя rkfixed. Обращение к ней производится через оператор присвоения какой либо переменной (например z) имени программы:
z:= rkfixed (X,0,tk,N,D), (6.18)
где: x – вектор переменных состояния, размер которого определяется вектором начальных значений x(0); и соответствует числу уравнений состояния; 0 и tk начало и конец временного интервала интегрирования; N – число точек на интервале интегрирования; D – функция, которая описывает правую часть уравнений, разрешенных относительно первых производных.
Для линейных цепей функция D имеет вид линейного матричного преобразования
D(t, x)=Ax+F. (6.19)
Все элементы матриц А и F должны быть определены перед обращением к программе rkfixed.
Решение получаем в виде матрицы z, где первый столбец соответствует дискретным значениям времени t. Остальные столбцы соответствуют значения переменного состояния.
Пример решения системы уравнений с помощью программы MathCAD приводиться внизу (рис. 6.7). Полная распечатка решения уравнения приводится в приложении 5.
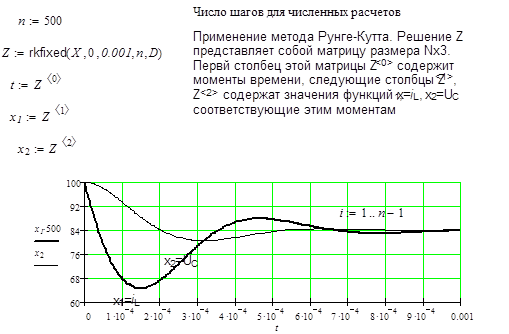 |
Рис 6.7
Задание 7. РАСЧЕТ НЕЛИНЕЙНЫХ ЦЕПЕЙ
Исходные данные:
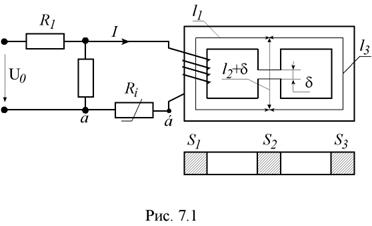 |
Катушка с ферромагнитным сердечником, имеющаячисло витков w, включена в цепь, питаемую источником постоянного напряжения U (pис. 7.1). Параметры схемы: R1 = 4 Ом,R2 =5 Ом; катушка намотана проводом, каждый виток которого имеет сопротивление
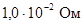 ; таким образом, сопротивление провода катушки, имеющей
; таким образом, сопротивление провода катушки, имеющей 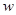 витков равно
витков равно 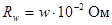 .
. Вольт - амперная характеристика нелинейного резистора Rн аппроксимируется выражением Uн=aI2н. Значения коэффициента 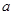 для различных учебных групп а1=8В/A2, а 2= 10B/A2, a 3= 12B/А2.
для различных учебных групп а1=8В/A2, а 2= 10B/A2, a 3= 12B/А2.
Величина напряжения источника, число витков катушки и геометрические размеры однородного ферромагнитного сердечника для каждого варианта приведены в табл.7.1. При этом, для ветви с зазором 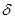 , под l подразумевается суммарная длина ее стальных участков (без зазора).
, под l подразумевается суммарная длина ее стальных участков (без зазора).
Кривая намагничивания материала сердечника приведена в табл.7.2.
Таблица 7.1.
| Вариант | U0, В | W витков | Обмотка находится на ветви | l 1, см | l 2, см | l 3, см | S 1, см2 | S 2, см2 | S 3, см2 | 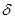 , мм , мм | Зазор устроен в ветви |
| 5,7 | 3.9 | 9.5 | 0,5 | ||||||||
| 8,5 | 15,4 | 10,4 | 0,3 | ||||||||
| 12.5 | 0,35 | ||||||||||
| 2,7 | 7,8 | 0,1 | |||||||||
| 4,3 | 0,25 | ||||||||||
| 36,5 | 0,5 | ||||||||||
| 18.5 | 14,4 | 10,5 | |||||||||
| 0,12 | |||||||||||
| 13,5 | 4,32 | 19.8 | 2,5 | 1,9 | 1,75 | 0,1 | |||||
| 7,6 | 0.52 | ||||||||||
| 6,15 | 3,9 | 0,15 | |||||||||
| 9.4 | 10,3 | 0,21 | |||||||||
| 8,8 | 0,25 | ||||||||||
| 7.4 | 19,5 | 24,2 | 7,7 | 2,1 | 3,8 | 0,1 | |||||
| 0,18 | |||||||||||
| 4,1 | 5,8 | 3,8 | 0,25 | ||||||||
| 14,6 | 10,2 | 0,15 | |||||||||
| 29,2 | 0,3 | ||||||||||
| 16,2 | 29,8 | 8,2 | 2,2 | 4,8 | 0,1 | ||||||
| 9,3 | 0,2 | ||||||||||
| 4,1 | 4,15 | 0,5 | |||||||||
| 4,9 | 15,6 | 10,3 | 0,25 | ||||||||
| 7,2 | 66,5 | 0,4 | |||||||||
| 35,7 | 42,5 | 40,5 | 2,4 | 0,1 | |||||||
| 37,6 | 0,35 | ||||||||||
| 28,5 | 5,8 | 9,6 | 0,6 | ||||||||
| 0,18 | |||||||||||
| 1,3 | |||||||||||
| 3,03 | 4,8 | 0,11 | |||||||||
| 4,4 | 0,28 |
Таблица 7.2
| Н | А/м | ||||||||||||
| В | Тл | 0,08 | 0,22 | 0,75 | 0,93 | 1,02 | 1,14 | 1,38 | 1,47 | 1,53 | 1,57 | 1,61 |
Требуется:
1. Найти магнитные потоки в ветвях ферромагнитного сердечника методом графического суммирования вебер-амперных характеристик.
2. Проверить полученные результаты путем решения обратной задачи.
3. Найти статическую индуктивность катушки при заданном токе.
 2015-05-26
2015-05-26 14927
14927
