Федеральное агентство по образованию
VII. Схема проверки гипотезы о значимости коэффициента корреляции.
VI. Схема проверки гипотезы о равенстве дисперсий двух нормальных СВ.
V. Схема проверки гипотезы о равенстве математических ожиданий двух нормальных СВ при неизвестных дисперсиях.
IV. Схема проверки гипотезы о равенстве двух нормальных СВ при известных дисперсиях.
II. Схема проверки гипотезы о математическом ожидании нормальной СВ при неизвестной дисперсии.
I. Схема проверки гипотезы о математическом ожидании нормальной СВ при известной дисперсии.
Пусть генеральная совокупность 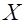 распределена нормально, причем ее математическое ожидание
распределена нормально, причем ее математическое ожидание 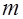 неизвестно, а дисперсия
неизвестно, а дисперсия 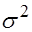 известна.
известна.
Также есть основания предполагать, что 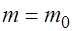 .
.
Тогда
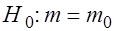
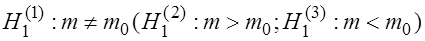
Для проверки 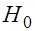 извлекается выборка объема
извлекается выборка объема 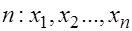 и в качестве критерия строится статистика
и в качестве критерия строится статистика
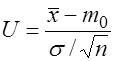 (1)
(1)
где 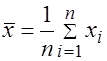 ,
, 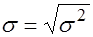 .
.
Доказано, что если гипотеза 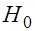 справедлива, то статистика U имеет стандартизированное нормальное распределение
справедлива, то статистика U имеет стандартизированное нормальное распределение 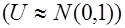 .
.
1. Пусть в качестве альтернативной рассматривается гипотеза:

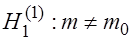 . Тогда критические точки
. Тогда критические точки 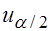 и
и 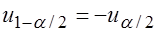 будут определяться по таблице значений функции Лапласа из условия
будут определяться по таблице значений функции Лапласа из условия
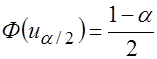
Если 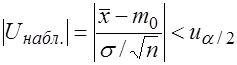 - нет оснований для отклонения
- нет оснований для отклонения 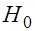 .
.
Если 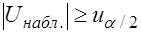 - гипотеза
- гипотеза 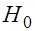 отклоняется в пользу альтернативной гипотезы
отклоняется в пользу альтернативной гипотезы 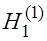 .
.
2. При 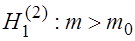 критическую точку
критическую точку 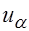 правосторонней критической области находят из равенства
правосторонней критической области находят из равенства
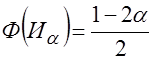
Если 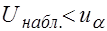 - нет оснований для отклонения
- нет оснований для отклонения 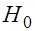 .
.
Если 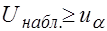 -
- 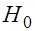 отклоняют в пользу
отклоняют в пользу 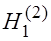 .
.
2. При 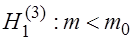 критическая точка
критическая точка 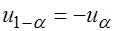 .
.
Если 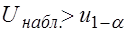 - нет оснований для отклонения
- нет оснований для отклонения 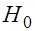 .
.
Если 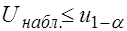 -
- 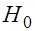 отклоняют в пользу
отклоняют в пользу 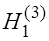 .
.
Пусть генеральная совокупность 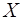 имеет нормальное распределение, причем ее математическое ожидание
имеет нормальное распределение, причем ее математическое ожидание 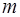 и дисперсия
и дисперсия 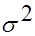 неизвестны.
неизвестны.
Пусть есть основания утверждать, что 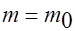 . Тогда строятся следующие гипотезы:
. Тогда строятся следующие гипотезы:
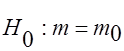
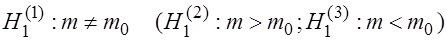 .
.
Для проверки  извлекается выборка объема
извлекается выборка объема 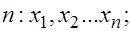 вычисляются выборочное среднее
вычисляются выборочное среднее
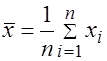 ;
;
исправленная выборочная дисперсия
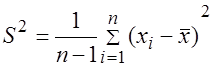 ;
;
Далее строится 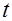 - статистика:
- статистика:
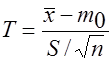 , (2)
, (2)
имеющая при справедливости  распределение Стьюдента с
распределение Стьюдента с 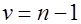 степенями свободы. Критическая область строится в зависимости от вида альтернативной гипотезы так же, как и в предыдущем разделе.
степенями свободы. Критическая область строится в зависимости от вида альтернативной гипотезы так же, как и в предыдущем разделе.
1. При 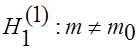 по таблице критических точек распределения значимости
по таблице критических точек распределения значимости 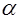 и числу степеней свободы
и числу степеней свободы 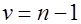 находятся критические точки:
находятся критические точки:
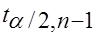 и
и 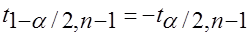 .
.
Если 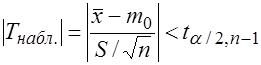 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 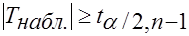 -
-  отклоняют в пользу
отклоняют в пользу 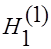 .
.
2. При 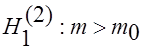 определяют критическую точку
определяют критическую точку 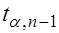 правосторонней критической области.
правосторонней критической области.
Если 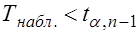 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 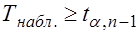 -
-  отклоняется в пользу
отклоняется в пользу 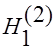 .
.
3. При 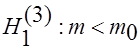 определяют критическую точку
определяют критическую точку 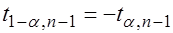 левосторонней критической области.
левосторонней критической области.
Если 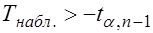 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 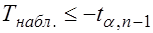 -
-  отклоняется в пользу
отклоняется в пользу 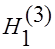 .
.
III. Схема проверки гипотезы о величине дисперсии нормальной СВ.
Принятие того или иного решения в экономике часть связано с анализом возможных результатов, точнее разбросе возможных результатов.
Здесь приходится иметь дело с выдвижением и проверкой гипотез о величине дисперсии.
Пусть случайная величина X ~ N (m, σ2);
X ~ N (m, σ2); 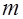 и
и 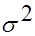 неизвестны. Проверяется гипотеза о равенстве дисперсии
неизвестны. Проверяется гипотеза о равенстве дисперсии 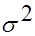 нормально распределенной генеральной совокупности
нормально распределенной генеральной совокупности 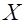 предполагаемому значению
предполагаемому значению 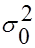 . Тогда:
. Тогда:
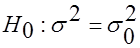
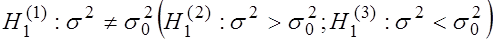 .
.
Для проверки  извлекается выборка объема
извлекается выборка объема 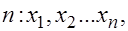 вычисляются выборочное среднее
вычисляются выборочное среднее 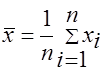 , исправленная выборочная дисперсия
, исправленная выборочная дисперсия 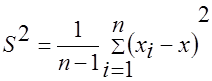 .
.
Тогда критерий проверки  имеет вид:
имеет вид:
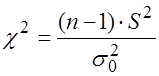 (3)
(3)
При справедливости  построенная статистика
построенная статистика 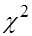 имеет
имеет 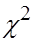 - распределение с
- распределение с 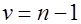 степенями свободы.
степенями свободы.
1. При 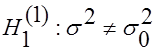 по таблице критических точек
по таблице критических точек 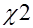 - распределения по заданному уровню значимости
- распределения по заданному уровню значимости 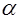 и числу степеней свободы
и числу степеней свободы 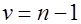 находят критические точки
находят критические точки 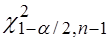 и
и 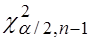 двусторонней критической области.
двусторонней критической области.
Если 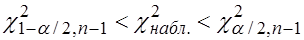 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 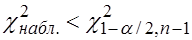 или
или 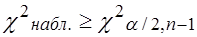 -
-  отклоняется в пользу
отклоняется в пользу 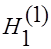 .
.
2. При 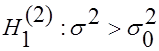 определяют критическую точку
определяют критическую точку 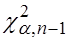 правосторонней критической области.
правосторонней критической области.
Если 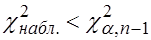 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 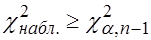 -
-  отклоняется в пользу
отклоняется в пользу 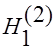 .
.
3. При 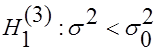 находят критическую точку
находят критическую точку 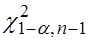 левосторонней критической области.
левосторонней критической области.
Если 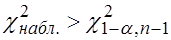 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 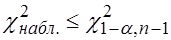 -
-  отклоняется в пользу
отклоняется в пользу 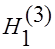 .
.
Пусть X ~ N (mx, σx2) и Y ~ N (my, σy2), причем их дисперсии 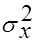 и
и 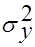 - известны (из предыдущих наблюдений или определены теоретически).
- известны (из предыдущих наблюдений или определены теоретически).
По двум выборкам 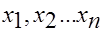 и
и 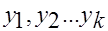 объемов
объемов 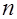 и
и 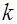 соответственно необходимо проверить гипотезу
соответственно необходимо проверить гипотезу 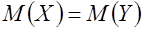 , т.е.
, т.е.
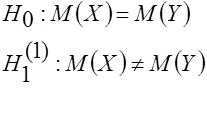
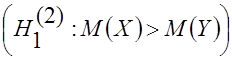
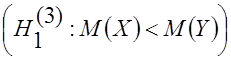 .
.
В качестве критерия проверки  принимается СВ U:
принимается СВ U:
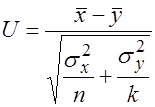 (4)
(4)
При справедливости  СВ U ~ N (0, 1).
СВ U ~ N (0, 1).
1. При 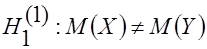 по таблице функции Лапласа определяют 2 критические точки
по таблице функции Лапласа определяют 2 критические точки 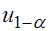 и
и 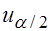 из условий:
из условий:
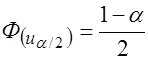 ,
, 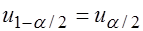 .
.
Если 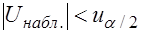 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 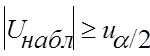 -
-  отклоняется в пользу
отклоняется в пользу 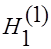 .
.
2. При 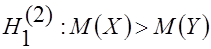 критическую точку
критическую точку 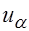 правосторонней критической области находят их равенства:
правосторонней критической области находят их равенства: 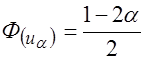 .
.
Если 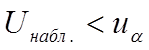 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 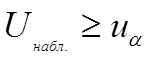 -
-  отклоняется в пользу
отклоняется в пользу 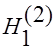 .
.
3. При 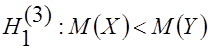 критическая точка
критическая точка 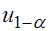 левосторонней критической области определяется из соотношения
левосторонней критической области определяется из соотношения 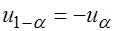 .
.
Если 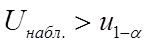 - нет оснований для отклонения
- нет оснований для отклонения  .
.
Если 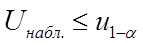 -
-  отклоняется в пользу
отклоняется в пользу 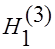 .
.
Пусть 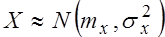 и
и 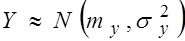 ,причем их дисперсии
,причем их дисперсии 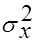 и
и 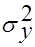 неизвестны. Выдвигается гипотеза о равенстве математических ожиданий:
неизвестны. Выдвигается гипотеза о равенстве математических ожиданий:
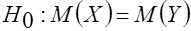
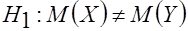
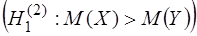 ;
;
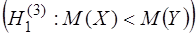 .
.
При этих условиях в качестве критерия проверки  принимают СВ
принимают СВ 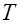 :
:
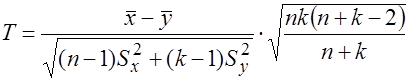 (5)
(5)
где 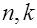 - объемы выборок
- объемы выборок 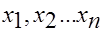 и
и 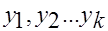 соответственно
соответственно 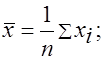
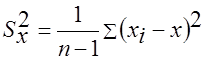 ,
,
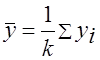 ;
; 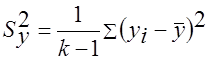 .
.
При справедливости  построенная статистика
построенная статистика 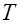 имеет
имеет 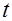 -распределение Стьюдента с
-распределение Стьюдента с 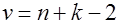 степенями свободы.
степенями свободы.
1. При 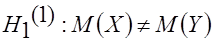 с помощью таблицы критических точек распределения Стьюдента по заданному уровню значимости α и числу степеней свободы
с помощью таблицы критических точек распределения Стьюдента по заданному уровню значимости α и числу степеней свободы 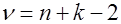 определяются критические точки
определяются критические точки 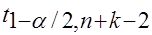 и
и 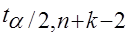 (
(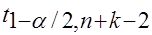 =
=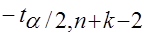 ) двусторонней критической области.
) двусторонней критической области.
Если 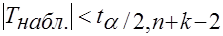 - нет оснований для отклонения Н0.
- нет оснований для отклонения Н0.
Если 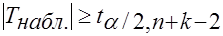 - Н0 отклоняется в пользу Н1(1).
- Н0 отклоняется в пользу Н1(1).
2. При 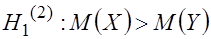 находят критическую точку
находят критическую точку 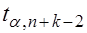 правосторонней критической области.
правосторонней критической области.
Если 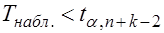 - нет оснований для отклонения Н0.
- нет оснований для отклонения Н0.
Если 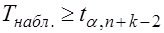 - Н0 отклоняется в пользу Н1(2).
- Н0 отклоняется в пользу Н1(2).
3. При 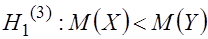 находят критическую точку левосторонней критической области
находят критическую точку левосторонней критической области 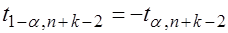 .
.
Если 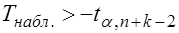 - нет оснований для отклонения Н0.
- нет оснований для отклонения Н0.
Если 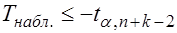 - Н0 отклоняется в пользу Н1(3).
- Н0 отклоняется в пользу Н1(3).
При сравнении двух экономических показателей иногда, в первую очередь, проводят анализ разброса значений рассматриваемых СВ. Например, при решении инвестирования в одну из отраслей остро стоит проблема риска вложений. При сравнивании уровня жизни двух стран среднедушевые доходы могут быть примерно одинаковы. Необходимо сопоставить разброс в доходах.
Анализ проводится путем сравнения дисперсий исследуемых СВ.
Пусть 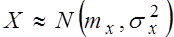 и
и 
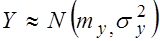 , причем их дисперсии
, причем их дисперсии 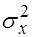 и
и 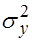 неизвестны. Выдвигается гипотеза о равенстве дисперсий
неизвестны. Выдвигается гипотеза о равенстве дисперсий 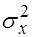 и
и 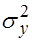 .
.
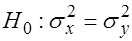
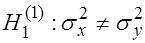
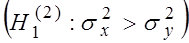 .
.
По независимым выборкам 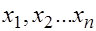 и
и 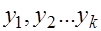 объемов
объемов 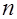 и
и 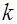 соответственно определяется:
соответственно определяется:
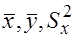 и
и 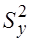 (для определенности пусть
(для определенности пусть 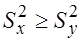 , в противном случае эти величины можно переобозначить).
, в противном случае эти величины можно переобозначить).
В качестве критерия проверки 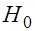 принимают СВ
принимают СВ
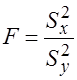 , (6)
, (6)
определяемую отношением большей исправленной выборочной дисперсии к меньшей.
Если 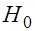 верна, то данная статистика
верна, то данная статистика 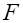 имеет
имеет 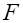 - распределение Фишера с
- распределение Фишера с 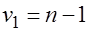 и
и 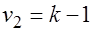 степенями свободы.
степенями свободы.
1. При 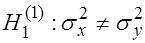 по таблицам критических точек распределения Фишера по уровню значимости
по таблицам критических точек распределения Фишера по уровню значимости 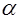 и числам степеней свободы
и числам степеней свободы 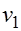 и
и 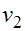 определяется критическая точка
определяется критическая точка 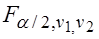 .
.
Если 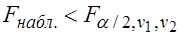 - нет оснований для отклонения
- нет оснований для отклонения 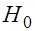 .
.
Если 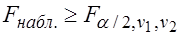 -
- 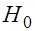 отклоняется в пользу
отклоняется в пользу 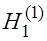 .
.
2. При 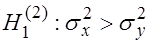 определяется критическая точка
определяется критическая точка 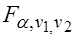 .
.
Если 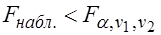 - нет оснований для отклонения
- нет оснований для отклонения 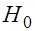 .
.
Если 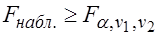 -
- 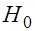 отклоняется в пользу
отклоняется в пользу 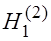 .
.
В основном, при проверке гипотезы о равенстве дисперсий в качестве альтернативной гипотезы в большинстве случаев используется гипотеза 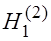 .
.
Одним из важнейших элементов эконометрического анализа является установление наличия связи между различными показателями (между ценой и спросом, доходом и потреблением, инфляцией и безработицей).
Обычно анализ начинают с простой линейной зависимости. Для того чтобы установить наличие значимой линейной связи между двумя СВ 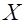 и
и 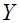 , следует проверить гипотезу о статистической значимости коэффициента корреляции. В этом случае используется следующая гипотеза:
, следует проверить гипотезу о статистической значимости коэффициента корреляции. В этом случае используется следующая гипотеза:
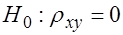
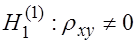 .
.
Для проверки 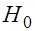 по выборке
по выборке 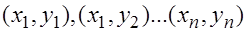 объема
объема 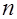 строится статистика:
строится статистика:
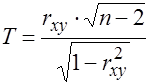 (7)
(7)
где 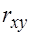 - выборочный коэффициент корреляции.
- выборочный коэффициент корреляции.
При справедливости 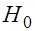 статистика
статистика 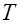 имеет распределение Стьюдента с
имеет распределение Стьюдента с 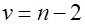 степенями свободы.
степенями свободы.
По таблице критических точек распределения Стьюдента по заданному уровню значимости 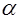 и числу степеней свободы
и числу степеней свободы 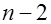 определяем критическую точку
определяем критическую точку 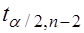 .
.
Если 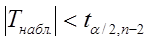 - то нет оснований для отклонения
- то нет оснований для отклонения 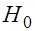 .
.
Если 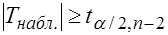 - то
- то 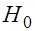 отклоняется в пользу альтернативной гипотезы
отклоняется в пользу альтернативной гипотезы 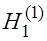 .
.
Если 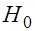 отклоняется, то фактически это означает, что коэффициент корреляции статистически значим (существенно отличен от нуля). Следовательно,
отклоняется, то фактически это означает, что коэффициент корреляции статистически значим (существенно отличен от нуля). Следовательно, 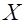 и
и 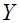 - коррелированны, т.е. между ними существует линейная связь.
- коррелированны, т.е. между ними существует линейная связь.
Список рекомендуемой литературы:
1. Эконометрика: Учебник / Под редакцией И.И.Елисеевой. – М.: Финансы и статистика, 2002
2. Практикум по эконометрике: Учебное пособие / И.И.Елисеева, С.В.Курышева, Н.М. Гордеенко и др.; Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2002
3. Магнус Я.Р., Катышев Л.К., Пересецкий А.А. Эконометрика. Начальный курс: Учебник. – 4 изд. – М.: Дело, 2000
4. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник для вузов: В 2 т. – М.: ЮНИТИ, 2001
5. Доугерти К. Введение в эконометрику. – М.: Инфра-М, 2001
6. Кулинич Е.И. Эконометрия. – М.: Финансы и статистика, 1999
7. Бородич С.А. Эконометрика: Учеб пособие / С.А. Бородич. – Мн.: Новое знание, 2001
8. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002
Государственное образовательное учреждение
высшего профессионального образования
«Братский государственный университет»
 2014-02-09
2014-02-09 1014
1014
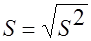 .
.






