Рядов. Адаптивное прогнозирование

Важное значение в анализе и прогнозировании на основе временных рядов имеют стационарные временные ряды, вероятностные свойства которых не изменяются во времени. Временной ряд 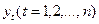называется строго стационарным, если совместное распределение вероятностей n наблюдений 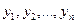такое же, как у n наблюдений 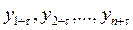(при любых n, t и τ). Свойства строго стационарных рядов не зависят от момента времени t.

Итак, для стационарного случайного процесса характерна неизменность во времени его основных вероятностных характеристик, таких, как математическое ожидание и дисперсия.

Под стационарными рядами понимаются однородные во времени случайные процессы, характеристики которых не меняются с течением времени t. Характеристики этих процессов и определяют особенности процессов и являются предметом исследования. Если эти характеристики (математическое ожидание, дисперсия и пр.) удалось с заданной степенью точности найти, то задача прогноза таких стационарных процессов становится чрезвычайно простой.

В то же время стационарные процессы могут иметь самый различный характер динамики – изменение одной части из них не имеет ярко выраженных тенденций во времени, динамика другой части имеет явно выраженную тенденцию изменения во времени, которая может носить и очень сложный нелинейный характер. Таким образом, стационарная группа типов динамики временного ряда может быть в свою очередь разделена на две подгруппы:

- простые стационарные;

- сложные стационарные.

Для первой группы факторов, простого стационарного типа, выполняется условие неизменности во времени их математического ожидания и других характеристик случайных процессов.

Если же математическое ожидание и иные характеристики вероятностного процесса претерпевает изменение во времени, то такие ряды являются сложными стационарными.

Простые стационарные процессы применительно к социально-экономическим объектам анализируются и прогнозируются с помощью простейших методов математической статистики (точечный и интервальный прогнозы динамики временного ряда). Чаще всего можно утверждать наличие закона нормального распределения и поэтому основные усилия должны быть направлены на доказательство этого положения с помощью соответствующих статистических гипотез и методов их проверки, а после этого – на вычисление характеристик процесса. Если удалось подтвердить гипотезу о нормальном характере распределения изучаемого ряда, то лучшей оценкой его математического ожидания выступает средняя арифметическая, а лучшей оценкой дисперсии – выборочная дисперсия. Причём, здесь уместен основной принцип выборочного метода – чем больше наблюдений, тем лучше оценки модели.

Сложные стационарные процессы свидетельствуют о наличии множества факторов, воздействующих на объект, показатели которого меняются во времени. Поэтому задачей прогнозиста является выявление главных из этих факторов и построение модели, описывающей влияние этих факторов на объект прогнозирования. Если этих факторов много, и выделить главные по каким-то соображениям невозможно, считают, что время выступает таким обобщающим фактором, и находят модель зависимости между прогнозным показателем и временем.

Как правило, в этих случаях исследователю неизвестно большинство основных характеристик случайного динамического стационарного процесса. Он должен по данным наблюдений за процессом найти эти характеристики. Здесь исследователь вынужден прибегать к некоторым априорным предположениям - допускать наличие того или иного закона распределения вероятностей, свойств процесса и его взаимосвязей, характера динамики и т.п. В данном случае наиболее эффективно может использоваться тот раздел экономической науки, который получил название эконометрики. Так как статистические свойства сложных стационарных рядов не изменяются со временем, то эти их свойства можно накопить и выявить с помощью вычисления некоторых функций от данных. Функция, которую впервые использовали для этой цели, является автоковариационной функцией.

Степень тесноты связи между последовательностями наблюдений временного ряда 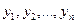и 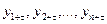обычно определяют с помощью выборочного коэффициента корреляции r(τ). Его формула приведена ниже:

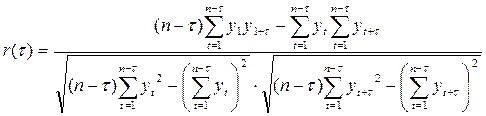, (6.5)

где τ - число периодов, по которым рассчитывается коэффициент автокорреляции (лаг).

Этот коэффициент оценивает корреляцию между уровнями одного и того же ряда, поэтому иногда его называют коэффициентом автокорреляции. Формула расчета коэффициент автокорреляции уровней ряда первого порядка (при τ=1) выглядит следующим образом (6.6):

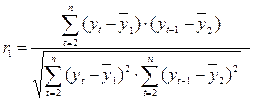, (6.6)

где 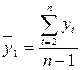, 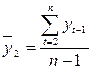; (6.7)

коэффициент автокорреляции уровней ряда второго порядка (6.8):

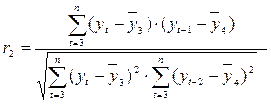, (6.8)

где 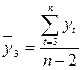; 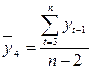. (6.9)

С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Считается целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило – максимальный лаг должен быть не больше n/6.

Функция r(τ) называется выборочной автокорреляционной функцией, а ее график – коррелограммой. Вид выборочной автокорреляционной функции (АКФ) тесно связан со структурой ряда.

1. Автокорреляционная функция r _τ для «белого шума», при τ >0, также образует стационарный временной ряд со средним значением 0.

2. Для стационарного ряда АКФ быстро убывает с ростом τ. При наличии отчетливого тренда автокорреляционная функция приобретает характерный вид очень медленно спадающей кривой.

3. В случае выраженной сезонности в графике АКФ также присутствуют выбросы для запаздываний, кратных периоду сезонности, но эти выбросы могут быть завуалированы присутствием тренда или большой дисперсией случайной компоненты.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка 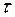, то ряд содержит циклические колебания с периодичностью в 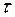моментов времени.

Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты и циклической (сезонной) компоненты.

Таким образом, при изучении сложных стационарных временных рядов основной задачей является выявление и устранение автокорреляции.

Нестационарные процессы, в противоположность стационарным, отличаются тем, что они меняют во времени все свои характеристики, причем это изменение может быть столь существенным, что динамика одного показателя, будет отражать развитие совершенно разных процессов. Все взаимосвязи и взаимозависимости объекта прогнозирования меняются во времени. Более того, меняется во времени состав, структура и направление взаимодействия элементов, составляющих объект прогнозирования.

В зависимости от того, насколько меняются во времени приращения ∆Y(T), нестационарные процессы также могут быть выделены в две подгруппы: эволюционные процессы; хаотические процессы.

Если приращения ∆Y(T) постепенно нарастают с течением времени, в результате количественных и качественных изменений, происходящих в системе, чей реализацией является нестационарный ряд, то эти процессы могут быть названы эволюционными. При этом отношение ∆Y(T) / Y(t+T), характеризующее нарастание неопределенности, имеет увеличивающуюся со временем Т динамику - от нуля до бесконечности. В случае, когда приращения ∆Y(T) не имеют какой-либо достаточно гладкой тенденции во времени и их изменения хаотичны (например, на первом же наблюдении ∆Y(T) может быть достаточно велико в сравнении с самим показателем ∆Y(T)), то такие процессы могут быть отнесены к хаотическим.

Хаотический характер динамики возникает в тех случаях, когда или сам процесс не инерционен и легко меняет под воздействием внешних или внутренних факторов динамику развития, или же когда на инерционный процесс воздействуют внешние факторы такой силы, что под их воздействием ломаются и внутренняя структура процесса, и его взаимосвязи, и его динамика. Иначе говоря, эволюционная динамика характеризует процесс адаптации объекта к внешним и внутренним воздействиям, а хаотическая динамика - отсутствие способности объекта к адаптации.

Сложный характер нестационарной динамики предопределяет и сложность аппарата моделирования и прогнозирования этой динамики.

Прогнозирование эволюционных составляющих экономической конъюнктуры до последнего времени не попадало в поле зрения специалистов по социально-экономическому прогнозированию – только в последние годы в учебники по прогнозированию стали включаться соответствующие разделы. На практике эволюционные процессы просто не выделяли в отдельную группу и для их анализа и прогнозирования использовали приемы классической эконометрии, не задумываясь над корректностью такого применения. Именно использование аппарата прогнозирования методологически несовместимого со свойствами объекта прогнозирования и приводит к возникновению серьезных ошибок инструментария и существенной дисперсии прогноза в практике прогнозирования социально-экономической динамики. Для прогнозирования временных рядов социально-экономических показателей эволюционного типа методологически обоснованным является применение адаптивных методов прогнозирования.

Вопросы прогнозирования хаотических рядов социально-экономической динамики в настоящее время решаются использованием теории хаоса и теории катастроф.

Далее рассмотрим методы прогнозирования часто наблюдаемых в практике социально-экономических исследований сложных стационарных и эволюционных нестационарных динамических процессов. Для рядов выше упомянутых типов статистиками Г.Е.П. Боксом и Г.М. Дженкинсом в середине 90-х годов прошлого века разработан алгоритм прогнозирования. В иерархию алгоритмов Бокса-Дженкинса входит несколько алгоритмов, самым известным и используемым из них является алгоритм ARIMA. Он встроен практически в любой специализированный пакет для прогнозирования. В классическом варианте ARIMA не используются независимые переменные. Модели опираются только на информацию, содержащуюся в предыстории прогнозируемых рядов, что ограничивает возможности алгоритма. В настоящее время в научной литературе часто упоминаются варианты моделей ARIMA, позволяющие учитывать независимые переменные.

Модели ARIMA опираются, в основном, на автокорреляционную структуру данных. В методологии ARIMA не предусматривается какой-либо четкой модели для прогнозирования данного временного ряда. Задается лишь общий класс моделей, которые описывают временной ряд и, которые позволяют как-то выражать текущее значение переменной через ее предыдущие значения. Потом алгоритм, подставляя внутренние параметры, сам избирает наиболее пригодную модель прогнозирования. Существует целая иерархия моделей Бокса-Дженкинса. Логично ее можно определить так:

AR(p)+MA(q)→ARMA(p,q)→ARMA(p,q)(P,Q)→ARIMA(p,q,r)(P,Q,R) →... (6.10)

где AR(p) – авторегрессионная модель с порядком р;

MA(q) - модель скользящей средней остатков порядка q;

ARMA(p,q) - комбинированная модель авторегрессии и скользящей средней;

ARMA(p,q)(P,Q) – модель экспоненциального сглаживания;

ARIMA(p,q,r)(P,Q,R) – моделированиенестационарного эволюционного процесса с линейным трендом;

ARIMA(p,q,r)(Ps,Qs,Rs) - мультипликативная модель сезонного процесса.

Первые три модели аппроксимируют динамику сложных стационарных временных рядов, последующие две – динамику эволюционных нестационарных временных рядов.

Модель считается приемлемой, если остатки, в основном, малые, распределенные случайно, и не содержат полезной информации. Если заданная модель не удовлетворительна, процесс повторяется, но уже с использованием новой улучшившей модели. Подобная итерационная процедура повторяется до тех пор, пока не будет найденной удовлетворительной модели. Из этого момента заданная модель может использоваться для целей прогнозирования.

В модели ARIMA уровень динамического ряда y_t определяется как взвешенная сумма предыдущих его значений и значений остатков ε_t – текущих и предыдущих. Она объединяет модель авторегрессии порядка р и модель скользящей средней остатков порядка q. Тренд включается в ARIMA с помощью оператора конечных разностей ряда y_t. Для фильтрации линейного тренда используют разницы первого порядка, для фильтрации параболического тренда – разницы второго порядка и т.д. Разница d должна быть стационарной. Вид модели ARIMA, адекватность ее реальному процессу и прогнозные свойства зависят от порядка авторегрессии р и порядка скользящей средней q. Ключевым моментом моделирования считается процедура идентификации – обоснования вида модели. В стандартной методике ARIMA идентификация сводится к визуальному анализу автокоррелограмм и основывается на принципе экономии, по которому (p + q) <= 2. Модель ARIMA порядка (р,d,q) достаточно гибкая и описывает широкий спектр несезонных процессов. При наличии сезонных колебаний в модели учитывается их периодичность с лагом s (для квартальных данных s = 4, для помесячных s = 12), и аналогичного смысла параметрами (Ps,Ds,Qs).

Таким образом, идентификацией временного ряда называется построение для ряда остатков адекватной модели, в которой остатки представляют собой «белый шум», а все регрессоры значимы.

Рассмотрим некоторые модели ARIMA подробнее.

Авторегрессионная модель порядка р имеет вид:

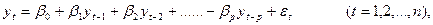(6.11)

где β₀,β_i,…,β_p – некоторые константы;

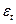- уровень «белого шума», который может быть опущен.

Если исследуемый процесс y_t в момент t определяется его значениями только в предыдущий период t-1, то получаем авторегрессионную модель 1-го порядка (6.11):

(6.12)

В моделях скользящей средней моделируемая величина задается линейной функцией от возмущений (остатков) в предыдущие моменты времени. Модель скользящей средней порядка q имеет вид:

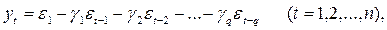(6.13)

где γ ₀, γ _i,…, γ _p – некоторые константы; ε – ошибки.

Нередко используется комбинированная модель авторегрессии и скользящей средней, которая имеет вид:

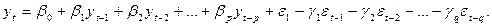(6.14)

Параметры p и q можно выбрать по следующим правилам:

1. Один параметр (p), если автокорреляционная функция (АКФ) экспоненциально убывает;

2. Два параметра авторегрессии (p), если АКФ имеет форму синусоиды или экспоненциально убывает;

3. Один параметр скользящего среднего (q), если АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций на других лагах;

6. Два параметра скользящего среднего (q), если АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах.

При изучении нестационарных эволюционных временных рядов применяется адаптивное прогнозирование.

Адаптивные методы прогнозирования - это совокупность моделей дисконтирования данных, способные приспосабливать свою структуру и параметры к изменению условий.

При оценке параметров адаптивных моделей наблюдениям (уровням ряда) присваиваются различные веса в зависимости от того, насколько сильным признается их влияние на текущий уровень. Это позволяет учитывать изменения в тенденции, а также любые колебания, в которых прослеживается закономерность. Адаптивные методы прогнозирования представляют собой подбор и адаптацию на основании вновь поступившей информации моделей прогнозирования. К самым распространенным из них относится метод экспоненциального сглаживания и метод гармонических весов Хельвига

Метод экспоненциального сглаживания. Особенность его состоит в том, что в процедуре выравнивания каждого наблюдения используются только значения предыдущих уровней ряда динамики, взятых с определенным весом. Вес каждого наблюдения уменьшается по мере его удаления от момента, для которого определяется сглаженное значение. Сглаженное значение уровня ряда S_t на момент t определяется по формуле:

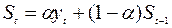, (6.15)

где S_t – значение экспоненциальной средней в момент t;

S_t-1 – значение экспоненциальной средней в момент (t-1);

Y_t – значение экономического процесса в момент времени t;

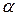- вес t – го значения ряда динамики (или параметр сглаживания ).

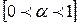Последовательное применение формулы (6.15) позволяет вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики. Кроме того, на основе формулы (6.15) определяются экспоненциальные средние первого порядка, то есть средние полученные непосредственно при сглаживании исходных данных ряда динамики. В тех случаях, когда тенденция после сглаживания исходного ряда определена недостаточно ясно, процедуру сглаживания повторяют, то есть вычисляют экспоненциальные средние 2-го, 3-го и т.д. порядков, пользуясь выражениями (6.16-6.18):

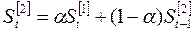; (6.16)

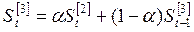; (6.17)

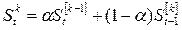, (6.18)

где 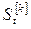- экспоненциальная средняя k -го порядка в точке t (k=1,2,3 …n).

Для линейной модели y_t=a₀+a₁t:

- начальные условия ;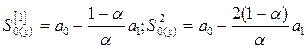

- экспоненциальные средние первого и второго порядка .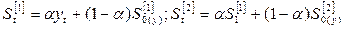

Прогноз осуществляется по формуле y_t^*=a₀+a₁t, где

a₀=2S_t^[1]-S_t^[2]; (6.19)

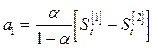. (6.20)

Ошибка прогноза определяется по формуле (6.22):

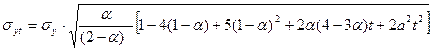, (6.21)

где 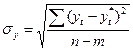- средняя квадратическая ошибка отклонения от линейного тренда;

(n-m) - число степеней свободы, определяемое в зависимости от числа членов ряда (n) и числа оцениваемых параметров выравнивающей кривой (m).

Метод гармонических весов. Этот метод был разработан польским статистиком З. Хельвигом. Он близок к методу простого экспоненциального сглаживания, использует тот же принцип. В его основе лежит взвешивание скользящего показателя, но вместо скользящей средней используется идея скользящего тренда. Экстраполяция проводится по скользящему тренду, отдельные тоски ломаной линии взвешиваются с помощью гармонических весов, что позволяет более поздним наблюдениям придавать больший вес. Метод гармонических весов базируется на следующих предпосылках:

- период времени, за который изучается экономический процесс, должен быть достаточно длительным, чтобы можно было определить его закономерности;

- исходный ряд динамики не должен иметь скачкообразных изменений;

- социально-экономическое явление должно обладать инерционностью, т.е. для наступления большого изменения в характеристиках процесса необходимо, чтобы прошло значительное время;

- отклонения от скользящего тренда имеют случайный характер;

- автокорреляционная функция, рассчитанная на основе последовательных разностей, должна уменьшаться с ростом t, т.е. влияние более поздней информации должно сильнее отражаться на прогнозируемой величине, чем на ранней информации.

Для получения точного прогноза метод гармонических весов необходимо выполнение всех вышеуказанных предпосылок для исходного ряда динамики. Для осуществления прогноза данным методом исходный ряд разбивается на фазы k. Число фаз должно быть меньше числа членов ряда n, то есть k<n. Обычно фаза равна 3-5 уровням. Для каждой фазы рассчитывается линейный тренд, то есть

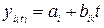(i=1,2,…..,n-k+1). (6.22)

При этом: для i=1, t=1,2, …., k; для i =2, t=2,3,….., k+1; для i= n-k+1, t= n-k+1, n-k+2, …, n.

Для оценки параметров a_i, b_ik используется метод наименьших квадратов.

С помощью полученных (n-k+1) уравнений определяются значения скользящего тренда. С этой целью выделяются те значения y_i(t), для которых t=i, их обозначают y_j(t). Пусть их будет n_j.

Затем находится среднее значение 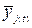по формуле (6.23):

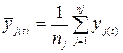, где j=1,2, …, n_j. (6.23)

После этого необходимо проверить гипотезу о том, что отклонения от скользящего тренда представляют собой стационарный процесс. С этой целью рассчитывается автокорреляционная функция. Если значения автокорреляционной функции уменьшаются от периода к периоду, то пятая предпосылка данного метода выполняется. Далее рассчитываются приросты по формуле (6.24):

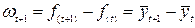. (6.24)

Средняя приростов вычисляется по формуле (6.25):

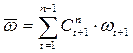, (6.25)

где 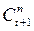– гармонические коэффициенты, удовлетворяющие следующим условиям: а) 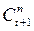>0 (t=1,2,….,n-1), б) .

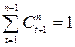Выражение (6.25) позволяет более поздней информации придавать большие веса, так как приросты обратно пропорциональны времени, которое отделяет раннюю информацию от поздней для момента t=n.

Если самая ранняя информация имеет вес 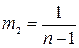, то вес информации, относящейся к следующему моменту времени, равен:

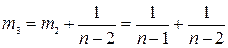. (6.26)

В общем виде ряд гармонических весов определяют:

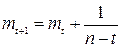(t=2,3,……,n-1), (6.27)

или

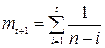(6.28)

отсюда

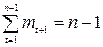. (6.29)

Чтобы получить гармонические коэффициенты 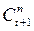_, удовлетворяющие двум выше указанным условиям, нужно гармонические веса m_t+1 разделить на (n-1), т.е.

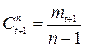. (6.30)

Далее прогнозирование производится так же, как и при простых методах прогноза, путем прибавления к последнему значению ряда динамики среднего прироста, то есть

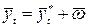(6.31)

при начальном условии .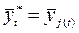

Данный метод прогнозирования применяется, когда есть уверенность, что тенденция в будущем описывается плавной кривой, то есть в ряду отсутствуют сезонные и циклические колебания. Таким образом, перед предвидением развития изучаемого объекта необходимо сделать вывод о стационарности или нестационарности временного ряда. Данное положение можно проверить с помощью теста Дики-Фуллера. Базовый порождающий данные процесс, который используется в тесте, — авторегрессионный процесс первого порядка:

y_t = m₀ + m₁×t + r×y_t–1 +ε_t, (6.32)

где m₀, m₁, r – постоянные коэффициенты, которые могут быть надены МНК; ε_t – случайная ошибка, которая в расчет может не приниматься.

В случае если выполняется условие: 0 < r < 1, то ряд является стационарным, в случаях: r £ 0; r ³ 1, то изучаемый временной ряд не является стационарным.