47969
Модуль суммы двух векторов можно вычислить, использую теорему косинусов: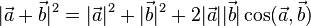 
, где 
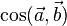— косинус угла между векторам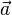и 
и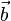 
.
Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: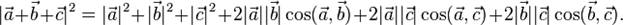 
Вычитание векторов
Для получения разности в координатной форме надо вычесть соответствующие координаты векторов: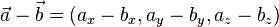 
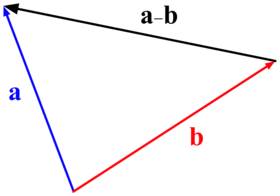
Модуль разности векторов
Три вектора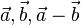 
, как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным: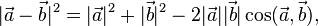 
Где 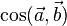— косинус угла между векторам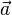и и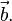 
Отличие от формулы модуля суммы в знаке перед косинусом, при этом надо хорошо следить, какой именно угол берется.
