2015-05-13
6789
§ 12.1. Теорема о существовании, непрерывности и дифференцируемости функции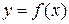 
, определяемой уравнением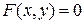 
Термин «неявная функция» относится к способу задания функциональной зависимости между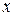 
и 
и 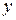означает, что вместо явной формулы 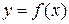эта зависимость представлена уравнением .
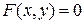Следует отметить, что уравнение 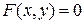не всегда определяет функцию 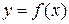. Например, уравнение 
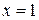функцию 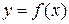не определяет. Кроме того, уравнение 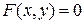не всегда позволяет однозначно выразить 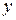через 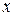. Например, уравнение 
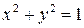, задающее окружность на плоскости, определяет при 
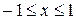две непрерывные функци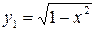и 
и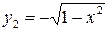 
.
В этом примере можно, например, дополнительно потребовать чтобы выполнялось неравенство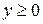 
. Тогда мы получим только .
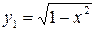В общей ситуации условия, при которых существует единственная функция 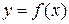, задаваемая уравнением 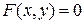, дает следующая теорема.
Теорема.12.1. Пусть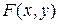 
определена и непрерывна вместе с частными производным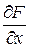и 
и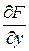 
в окрестности U точки 
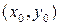такой, что 
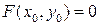и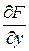 
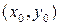
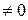. Тогда существуют числа 
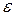и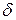 
такие, что на множестве 
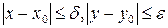уравнение 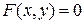равносильно уравнению 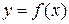где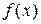 
непрерывная и дифференцируемая на 
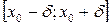функция, и 
.
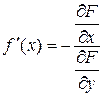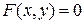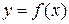Замечание. Равносильность и означает, что уравнение 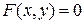однозначно определяет в рассматриваемой области дифференцируемую функцию 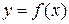такую, что 
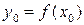, вообще, 
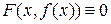при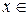 
.
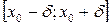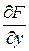
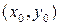
► По условию 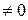. Пусть, для определенности,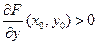 
(если это не так, то просто меняем знак у левой части исходного уравнения).
По условию, производная непрерывна в окрестности и сохраняет знак,
следовательно, найдётся такая окрестность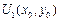 
всюду в пределах которой 
.
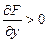Рассмотрим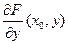 
, так как она положительна, 
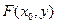возрастает для любых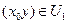 
Фиксируем положительное число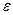 
можно подобрать положительные и отрицательные окрестности и выбрать из них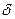 
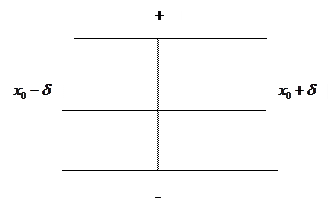
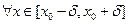Существует единственный 
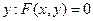. Каждому 
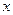сопоставим 
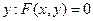. Назовем эту точку 
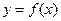. По построению мы получим непрерывную функцию 
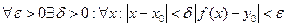Что равносильно тому, что как только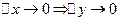 
Рассмотрим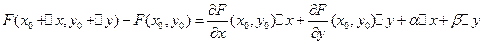 
Получаем равенство
◄
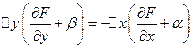
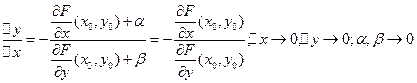Теорема Пусть функция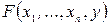 
непрерывна и имеет все непрерывные частные производные в окрестности точки 
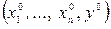такой, что 
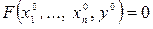, причем 
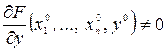. Тогда существуют числа 
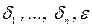такие, что в области 
, 
, 
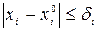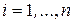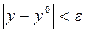уравнение 
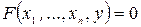равносильно уравнению 
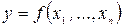, причем функция 
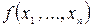непрерывна и имеет непрерывные частные производные, причем
.
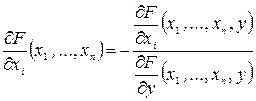2. Формулировка теоремы о существовании, непрерывности и дифференцируемости функции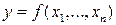 
определяемой уравнением 
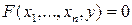. Формулировка теоремы о неявных функциях, определяемых системой уравнений
Теорема 19.2. Пусть функция 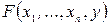непрерывна и имеет все непрерывные частные производные в окрестности точки 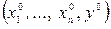такой, что 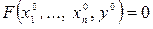, причем 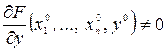. Тогда существуют числа 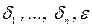такие, что в области 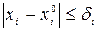, , 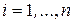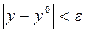уравнение 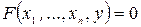равносильно уравнению 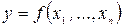, причем функция 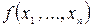непрерывна и имеет непрерывные частные производные, причем
.
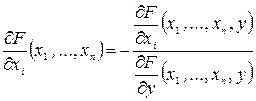►Доказывается так же, как и для случая ◄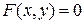
Рассмотрим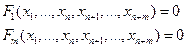 
Параметрическое задание поверхности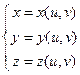 
При каких условиях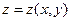 
и как найти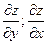 
Дифференцируем и получаем
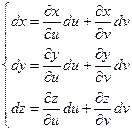
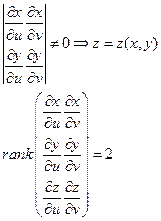
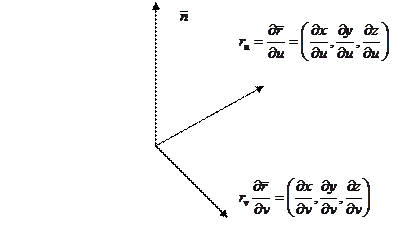
Ранг равен 2, следовательно, прямые не параллельны и образуют плоскость. Найдем нормаль к этой плоскости.
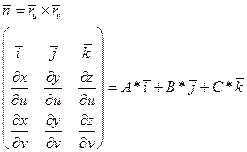
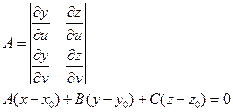
Либо такой вид билета.
Теорема Пусть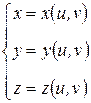 
, (2.1)
где функции , ,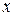 
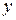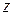непрерывны и имеют непрерывные производные в некоторой области 
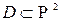(точки 
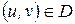). Пусть матрица Якоби 
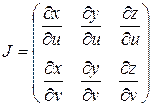имеет в этой области ранг 2. Тогда, если, например, минор 
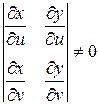, то в области 
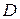систему можно преобразовать к уравнению
, 
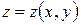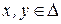, (2.2)
где 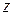есть непрерывно дифференцируемая функция от 
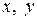в област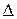и 
и
, 
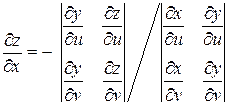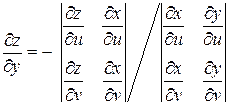, (2.3)
Замечание Уравнения (2.1) определяют в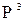 
некоторую поверхность 
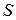и называются параметрическими уравнениямиэтой поверхности. Теорема утверждает, что поверхность 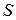есть график функции 
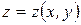((2.2)). Обозначают 
, 
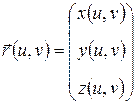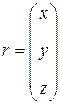и уравнения (2.1) принимают вид 
.
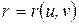Если зафиксировать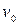 
, то 
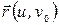– уравнение координатной линии на 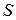(аналогично, 
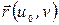при фиксированном 
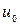также представляет собой уравнение координатной линии на 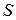). Векторы 
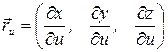и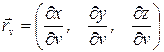 
– касательные векторы к координатным линиям. Если взять точку поверхности, соответствующую параметрам 
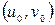и рассмотреть касательную плоскость в этой точке, то векторы 
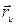и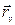 
лежат в этой плоскости. Если ранг матрицы 
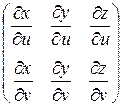равен 2, это означает, что 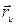и 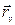не параллельны и их векторное произведение представляет собой нормальный вектор к касательной плоскости и
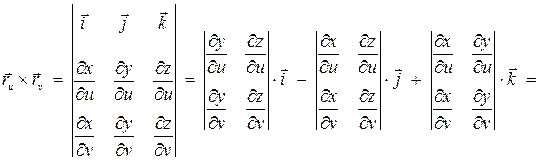
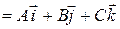, (2.4)
где буквы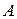 
, 
, 
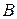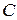обозначают соответствующие определители. В этих обозначениях формулы (2.3) принимают вид
, 
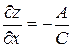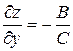, (2.5)
а единичный вектор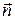 
нормали (2.4), получаемый при делении вектора на его модуль 
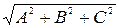, равен
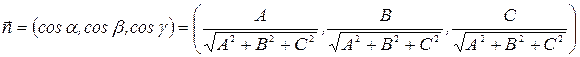(2.6)
Преобразуем выражение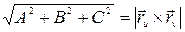 
. По определению векторного произведения, 
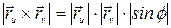, где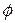 
– угол между 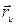и 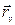. Тогда
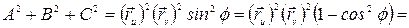
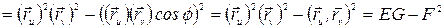, (2.7)
где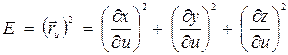 
, 
, 
.
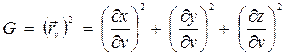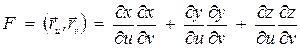Понятие независимости функций. Рассмотрим систему функций
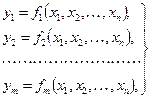(1)
определенных и непрерывных, вместе со своими частными производными, в некоторой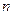 
-мерной открытой области D.
Рассмотрим случай, когда значение одной из них, например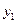 
, однозначно определяется совокупностью тех значений, которые принимают остальные функции
.
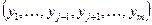Точнее говоря, если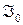 
есть множество таких 
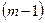-мерных точек, отвечающих всевозможным точкам 
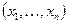в D, то предполагается что в 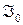будет иметь место функциональная зависимость
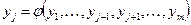, (2)
причем это равенство оказывается тождеством относительно 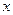в D, если вместо всех 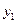, подставить функции (1). Тогда говорят, что в области D функция 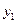зависит от остальных. Впрочем, для того, чтобы иметь возможность применять дифференциальное исчисление, мы включим в определение еще требование, чтобы функция 
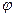была определена и непрерывна со своими частными производными в некоторой открытой области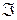 
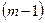-мерного пространства, содержащей множество .
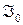Если, в частности, одна из функций (1),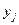 
, сводится к постоянной, то она явно будет зависеть от остальных: здесь можно просто положить 
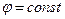. Функции 
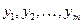называются вообще зависимыми в области D, если одна из них (все равно какая) зависит от остальных.
Примеры. 1) Если положить
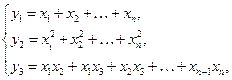
то нетрудно проверить, что во всем 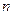-мерном пространстве будет выполняться тождество
.
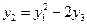2) Аналогично для функций
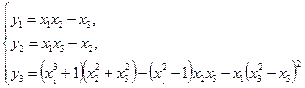
имеем тождественно (в трехмерном пространстве)
.
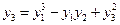Все это – зависимые функции.
Если ни в области D, ни в какой-либо частичной, в ней содержащейся, области не имеет место тождество вида (18), то функции 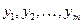называют независимыми в области D.
Ответ на вопрос о независимости функций дает рассмотрение так называемой матрицы Якоби, составленной из частных производных этих функций по всем независимым переменным:
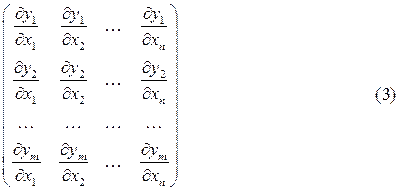
Предполагая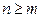 
, имеем такую теорему:
Теорема 1. Если хоть один определитель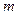 
-ого порядка, составленный из элементов матрицы (3), отличен от нуля в области D, то в этой области функции 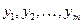независимы.
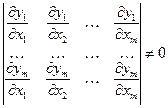. (4)
Если бы не равным нулю был не этот, а какой-нибудь другой определитель, то, изменив нумерацию переменных, можно было бы свести вопрос к случаю (4).
Доказательство теоремы будем вести от противного. Предположим, что одна из функций, например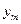 
, выражается через остальные, так что
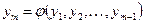, (5)
хотя бы в некоторой части D0 области D.
Продифференцировав это тождество по каждой из переменных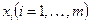 
, мы получим ряд тождеств (в D0) вида
.
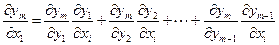
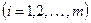Мы видим, что элементы последней строки определителя (5) получаются путем сложения соответственных элементов первых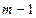 
строк, умноженных предварительно на множители 
, 
, 
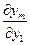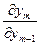. Такой определитель, как известно, равен нулю. Это противоречит условию теоремы. Полученное противоречие доказывает невозможность равенства (5).
