Общее уравнение плоскости. Преобразуем уравнение (1), раскроем скобки, на первое место выставим слагаемые, содержащие

Преобразуем уравнение (1), раскроем скобки, на первое место выставим слагаемые, содержащие :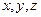

(**)

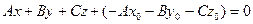свободный член 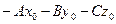принято обозначать D, т.е. 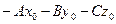= D, подставим в уравнение(**), получим:

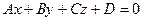(2)

где А,В,С – координаты нормального вектора, причем (А,В,С, D) 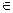Z, А>0.

Уравнение (2) называется общим уравнением плоскости.

Задача 1 Составить уравнение плоскости α, проходящей через точку N(2,-2,0) перпендикулярно вектору 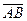: А(5,0,1), В(3,2,-2).

Решение

1 Плоскость проходит через точку N(2,-2,0).

2 Найдем нормальный вектор 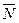плоскости α.

Т.к. вектор 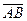перпендикулярен плоскости α по условию, то его можно рассматривать в качестве нормального вектора плоскости, т.е. 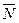= 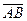. Найдем координаты вектора :

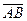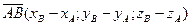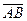, (-2, 2, -3), тогда 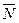(-2;2;-3).

3 Составим уравнение плоскости α.

Воспользуемся уравнением (1):

.

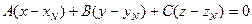Имеем

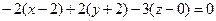
Преобразуем, полученное уравнение к общему виду:

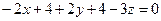
Умножим обе части уравнения на (-1), получим

.

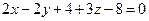Ответ: .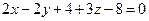

1.5 Исследование общего уравнения плоскости (таблица 2)

Таблица 2

Условия, определяющие плоскость	Вид уравнения	Определение плоскости	Графическое изображение
1	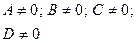	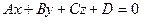Общее уравнение плоскости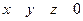
2	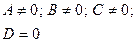	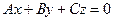Уравнение плоскости, проходящей через начало координат
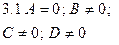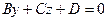		Уравнение плоскости, проходящей параллельно оси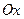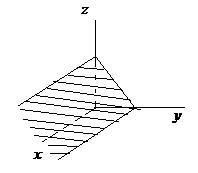
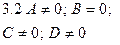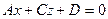		Уравнение плоскости, проходящей параллельно оси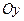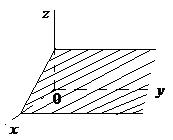
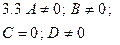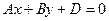		Уравнение плоскости, проходящей параллельно оси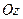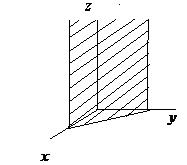
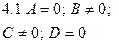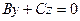		Уравнение плоскости, проходящей через ось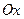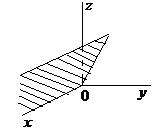

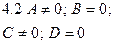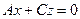		Уравнение плоскости, проходящей через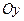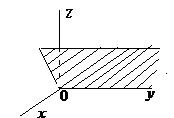
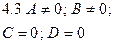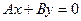		Уравнение плоскости, проходящей параллельно ось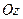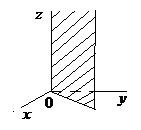
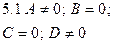	Ах + D = 0	Уравнение плоскости, проходящей параллельно координатной плоскости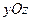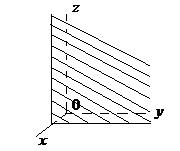
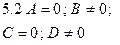	Ву + D = 0	Уравнение плоскости, проходящей параллельно координатной плоскости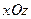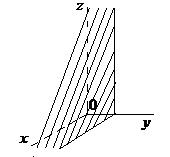
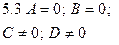	Сz + D = 0	Уравнение плоскости, проходящей параллельно координатной плоскости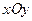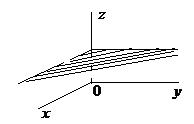
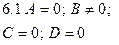	Ву = 0, у = 0	Уравнение координатной плоскости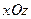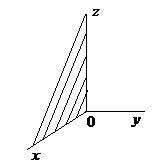

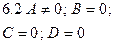	Ах = 0, х = 0	Уравнение координатной плоскости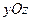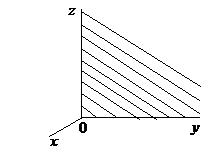
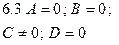	Сz = 0, z = 0	Уравнение координатной плоскости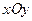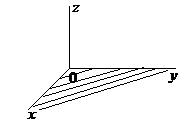

Замечание Графическое изображение плоскостей, представлено в первом октанте