МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
(образован в 1953 году)

Кафедра физики и высшей математики
| Дистанционное обучение | Физ. мат. 7. 11.2202 зчн. плн. Физ. мат. 7. 11.2202 зчн. скр. | Физ. мат. 7. 11.2202 очн.плн. Физ. мат. 7. 11.2202 очн. скр |
Ю.А. Зуев
Учебно-методические указания по проведению практических занятий для студентов специальности 230102 (2202) всех форм обучения.

Www.msta.ru
Москва – 2006
УДК 519.8
Ó Зуев Ю.А. Дискретная математика. Учебно-методические указания по проведению практических занятий для студентов специальности 230102(2202) всех форм обучения. М., МГУТУ, 2006.
В пособии представлены возможные варианты задач, решаемых на практических занятиях по курсу дискретной математики.
Автор: д.ф.-м.н., профессор Зуев Юрий Анатольевич
Рецензент: ст. преп. Садыкова А.Р.
Редактор: Свешникова Н.И.
ÓМосковский государственный университет технологий и управления, 2006.
109004, Москва, Земляной вал, 73.
СОДЕРЖАНИЕ
Предисловие……………………………………………………………………...4
Занятие 1. ………………………………………………………………………...5
Занятие 2………………………………………………………………………….5
Занятие 3………………………………………………………………………….6
Занятие 4………………………………………………………………………….7
Занятие 5………………………………………………………………………….8
Занятие 6……………………………………………………………………….....8
Занятие 7……………………………………………………………………….....9
Занятие 8…………………………………………………………………………11
Занятие 9…………………………………………………………………………11
Занятие 10…………………………………………………………………….….12
Литература……………………………………………………………………….14
Предисловие
Практические занятия по дискретной математике включают упражнения по теории перечисления, теории графов, включая важнейшие алгоритмы на графах, а также знакомство с принципами помехоустойчивого и криптографического кодирования. В процессе обучения у студента должны выработаться уверенные навыки работы с дискретными структурами, умение строить дискретные модели и решать с их помощью практические задачи. Графы, безусловно, являются важнейшими из подобных структур. Учащиеся должны в полной мере усвоить понятия теории графов и свободно оперировать ими. Основные алгоритмы на графах должны быть освоены настолько уверенно, что учащиеся должны быть в состоянии программно реализовать их на языках высокого уровня.
По плану на практические занятия отводится 50 часов. В соответствии со сложившийся практикой план составлен из расчета 10 пятичасовых занятий. За основу взята книга Ю.А. Зуева «Лекции по дискретной математике», М., МГУТУ, 2004.
Занятие 1 (5 часов)
Тема. Элементарная комбинаторика, перестановки, размещения сочетания и разбиения.
Цель. Познакомить студентов с основными комбинаторными понятиями, научить их пользоваться правилом произведения.
Теоретические вопросы. Число перестановок на 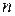 символах, число размещений, сочетаний и разбиений. Правило произведения для подсчета числа этих объектов и решения других комбинированных задач.
символах, число размещений, сочетаний и разбиений. Правило произведения для подсчета числа этих объектов и решения других комбинированных задач.
Методические указания. В качестве примера на правило произведения рассматривается следующая задача. В буфете имеется 4 ванильных, 2 шоколадных и 3 фруктовых пирожных. Сколько вариантов покупки существует? (Ничего не купить – тоже вариант покупки).
Решение. Имеется 5 вариантов покупки ванильных пирожных, 3 варианта – шоколадных и 4 – фруктовых. Поэтому в соответствии с правилом произведения число вариантов покупки равно
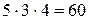 .
.
Задачи.
1. Пусть имеется 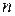 языков. Сколько нужно изучать словарей, чтобы был возможен перевод с любого языка на любой?
языков. Сколько нужно изучать словарей, чтобы был возможен перевод с любого языка на любой?
2. У мамы 5 яблок, 7 груш и 3 апельсина. Каждый день, в течение 15дней, она выдает сыну по одному фрукту. Сколькими способами это может быть сделано?
3. В распоряжении имеются яблоки, груши и апельсины. Сколькими способами может быть составлен подарочный набор из 5 фруктов?
4. Сколькими способами можно разделить яблоко, грушу, сливу, апельсин, лимон и айву между тремя мальчиками так, чтобы каждому досталось по 2 фрукта?
5. В турнире участвуют 2 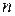 команд. Сколькими способами может быть проведен первый круг?
команд. Сколькими способами может быть проведен первый круг?
Занятие 2 (5 часов)
Тема. Бином Ньютона. Полиномиальная формула. Формула включения и исключения. Связь комбинаторики с теорией вероятностей.
Цель. Знакомство с важнейшими комбинаторными формулами. Приобретение навыков в решении элементарных задач по теории вероятностей с помощью комбинаторики.
Теоретические вопросы. Формулы для биномиальных и полиномиальных коэффициентов. Доказательство формулы включения и исключения. Классическое определение вероятности по Лапласу.
Методические указания. В качестве примера разберем задачу. Найти коэффициент при 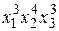 в разложении
в разложении 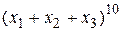 .
.
Решение. В соответствии с полиномиальной формулой этот коэффициент равен
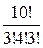
Другой пример, на вероятность. Какова вероятность при игре «в подкидного дурака» получить при сдаче 4 туза?
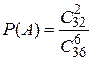 ,
,
так как 4 туза дополняются 2 картами, выбранными из остальных 32 карт.
Задачи.
1. Найти коэффициент при 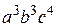 в разложении
в разложении 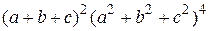 .
.
2. Найти коэффициент при  в разложении
в разложении  .
.
3. В группе, состоящей из 20 человек, 6 знают немецкий, 7 – французский и 8 – английский язык, 3 человека знают немецкий и французский, 4 – немецкий и английский, 5 – французский и английский и один человек знает все 3 языка. Сколько человек не знают ни одного иностранного языка?
4. Из перетасованной колоды извлекаются 4 карты. Какова вероятность, что будут извлечены 2 короля и 2 дамы?
5. Из конфетницы, содержащей 4 шоколадных конфеты и 8 карамелей, наугад берутся 2 конфеты. Какова вероятность, что обе они шоколадные?
Занятие 3 (5 часов)
Тема. Производящие функции и рекуррентные соотношения.
Цель. Ознакомление с методом производящих функций в комбинаторном анализе.
Теоретические вопросы. Производящая функция последовательности. Тождества для производящих функций.
Методические указания. Рассмотрим задачу. Найти число 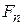 двоичных последовательностей длины
двоичных последовательностей длины 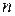 , не содержащих двух единиц подряд.
, не содержащих двух единиц подряд.
Решение. Имеем 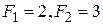 . Положим
. Положим 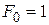 . Разобьем искомое множество последовательностей на 2 подмножества: последовательности, начинающейся с 0, и последовательности, начинающиеся с 1. Последовательности первого типа не имеют каких либо дополнительных ограничений на последующие
. Разобьем искомое множество последовательностей на 2 подмножества: последовательности, начинающейся с 0, и последовательности, начинающиеся с 1. Последовательности первого типа не имеют каких либо дополнительных ограничений на последующие 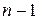 символов. Поэтому их
символов. Поэтому их 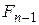 .
.
Последовательность второго типа на второй позиции обязана содержать 0, а на последующие 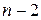 символов нет каких-либо ограничений, поэтому их
символов нет каких-либо ограничений, поэтому их 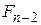 . Получаем рекуррентное соотношение
. Получаем рекуррентное соотношение
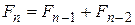 .
.
Домножаем обе части на 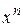 и суммируем по
и суммируем по 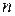 от 2 до
от 2 до 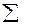 .
.
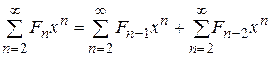
Это позволяет для производящей функции
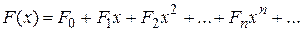
получить соотношение
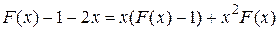 .
.
Откуда
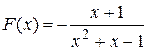 .
.
Разлагая на простейшие дроби, получаем
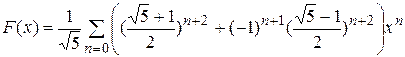 .
.
Откуда
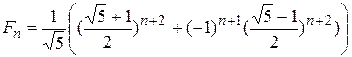 .
.
Задачи.
1. Найти 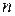 -ый член последовательности, заданной рекуррентно:
-ый член последовательности, заданной рекуррентно:
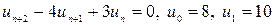 .
.
2. Найти 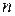 -ый член последовательности, заданной рекуррентно:
-ый член последовательности, заданной рекуррентно:
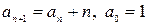 .
.
3. Найти 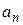 и
и 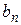 из системы рекуррентных соотношений
из системы рекуррентных соотношений
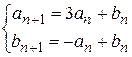 ,
, 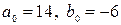 .
.
Занятие 4 (5 часов)
Тема. Перечисление в присутствии группы. Лемма Бернсайда и теорема Пойа.
Цель. Познакомить студентов с методами перечислений классов эквивалентности, возникающих в результате действия группы.
Теоретические вопросы. Группы, действие группы на множестве, орбиты, лемма Бернсайда, цикловой индекс, теорема Пойа.
Методические указания. Найдем цикловой индекс группы самосовмещений куба. Эта группа содержит 24 элемента, а именно:
1) тождественное вращение; циклическая структура 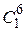 ;
;
2) 3 нетождественных вращения вокруг каждой из 3 осей, соединяющих середины противоположных граней, - итого 9 вращений; 3 – циклической структуры 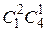 ;
;
3) 2 нетождественных вращения вокруг каждой из 4 осей, соединяющих противоположные вершины; циклическая структура 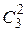 ;
;
4) 1 нетождественное вращение вокруг каждой из 6 осей, проходящих через середины противоположных ребер; циклическая структура 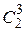 .
.
Цикловой индекс группы
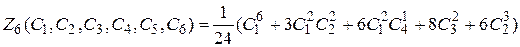 .
.
Задачи.
1. Найти цикловой индекс группы самосовмещений тетраэдра, действующей на множестве его граней.
2. Найти число различных раскрасок граней тетраэдра в 2 цвета, использующих каждый цвет дважды.
Занятие 5
Контрольная работа по перечислительной комбинаторике.
Примерный перечень задач.
1. Колода 36 карт случайным образом делится пополам. Какова вероятность, что в каждой половине будет по 2 туза?
2. Сколько диагоналей имеет правильный 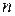 -угольник?
-угольник?
3. Восемь шаров случайным образом размещаются по 8 ящикам. Какова вероятность, что все ящики окажутся занятыми?
4. В разложении 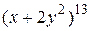 найти коэффициент при
найти коэффициент при 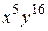 .
.
5. Какова вероятность, что среди 6 карт, полученных при сдаче в игре «в подкидного дурака» будут карты всех 4 мастей?
6. Найти формулу 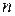 -го члена последовательности, заданной рекуррентно:
-го члена последовательности, заданной рекуррентно:
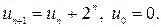
7. Сколько ожерелий можно составить из 7 бусинок, используя 3 красных бусинки и 4 синих?
Занятие 6 (5 часов)
Тема. Основные понятия теории графов.
Цель. Сделать понятие графа привычным для студента. Ознакомиться с различными видами графов, усвоить определения, научить использованию графов при моделировании прикладных задач.
Теоретические вопросы. Критерии двудольности, эйлеровости, эквивалентные определения дерева, понятия изоморфизма.
Методические указания. Студент должен уверенно оперировать такими понятиями как степень вершины графа, двудольные графы, понимать изоморфизм графов. В качестве примера можно предложить доказать изоморфность следующих графов:

 | |||
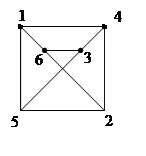 | |||
Изоморфизм между ними указывается с помощью данной на рисунке нумерации вершин.
Задачи.
1. Доказать, что в двудольном графе возможны только циклы четной длины.
2. Существует ли регулярный граф степени 3 с 5 вершинами?
3. Сколько ребер имеет лес с 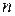 вершинами и
вершинами и 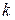 компонентами связности?
компонентами связности?
Занятие 7 (5 часов)
Тема. Основные алгоритмы в теории графов.
Цель. Ознакомление с экстремальными задачами на взвешенных графах. Усвоение понятия эффективности алгоритма. Изучение некоторых основных алгоритмов в теории графов и теории сетей.
Теоретические вопросы. Минимальное остовное дерево, кратчайший путь между двумя вершинами, паросочетания в двудольных графах, потоки в сетях.
Методические указания. Необходимо научить студента оценивать трудоемкость алгоритма с помощью символа 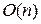 . Для нахождения минимального остовного дерева целесообразно давать как «жадный» алгоритм, так и правило ближайшего соседа. Для нахождения кратчайшего пути между вершинами используется алгоритм Дейкстры. Нахождение максимального паросочетания следует проводить как методом чередующейся цепи, так и методом потока в сети.
. Для нахождения минимального остовного дерева целесообразно давать как «жадный» алгоритм, так и правило ближайшего соседа. Для нахождения кратчайшего пути между вершинами используется алгоритм Дейкстры. Нахождение максимального паросочетания следует проводить как методом чередующейся цепи, так и методом потока в сети.
Задачи.
1. Найти минимальное остовное дерево с помощью:
а) «жадного» алгоритма;
б) правила ближайшего соседа.
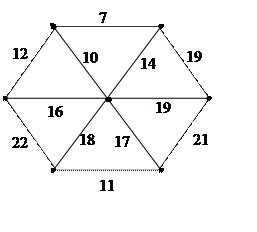 |
2. С помощью алгоритма Дейкстры найти кратчайший путь из вершины 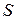 в вершину
в вершину 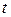 .
.

3. Методом чередующейся цепи достроить паросочетание до совершенного
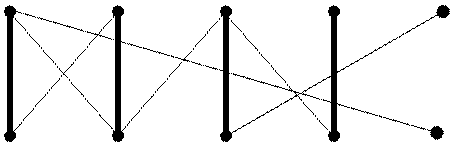 |
4. С помощью алгоритма Форда-Фалксрсона найти максимальный поток в сети из 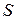 в
в  и минимальный разрез
и минимальный разрез
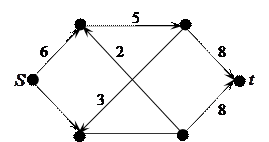
Занятие 8 (5 часов)
Тема. Метод «ветвей и границ» на примере задачи коммивояжера.
Цель. Познакомить студентов с важным подходом к решению дискретных экстремальных задач, применяемом в тех случаях, когда эффективного алгоритма для решения задачи неизвестно, а размеренность задачи невелика.
Теоретические вопросы. Постановка задачи коммивояжера, ее прикладные значения. Основная идея метода «ветвей и границ». Получение нижних оценок в задаче коммивояжера.
Методические указания. Решение задачи коммивояжера должно сопровождаться построением дерева решений, в каждой вершине которого записывается нижняя оценка решения. Кроме того, для наглядности около каждой вершины должен рисоваться ориентированный граф с отмеченными дугами, включаемыми в строящийся контур.
Задача.
Методом «ветвей и границ» решить симметричную задачу коммивояжера
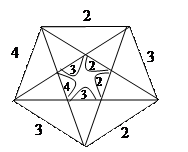 |
Решение подобных задач рассмотрено в 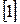 .
.
Занятие 9 (5 часов).
Тема. Помехоустойчивое кодирование.
Цель. Ознакомление с принципами помехоустойчивого кодирования информации.
Теоретические вопросы. Расстояние Хэмминга, конечные поля, линейное пространство над полем 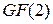 , линейные коды, порождающая и проверочная матрица, код Хэмминга.
, линейные коды, порождающая и проверочная матрица, код Хэмминга.
Методические указания. Приступая к данной теме целесообразно напомнить студентам сведения из линейной алгебры, касающиеся подпространства и его ортогонального дополнения, а также объяснить арифметические действия в поле 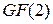 .
.
Задачи.
1. Пусть 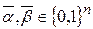 . Расстояние Хэмминга
. Расстояние Хэмминга 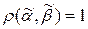 .
.
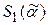 и
и 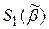 - шары Хэмминга, радиуса 1. Найти
- шары Хэмминга, радиуса 1. Найти 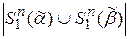 .
.
2. Найти проверочную матрицу для линейного кода с порождающей матрицей
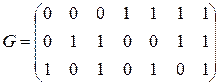 .
.
3. Найти кодовое расстояние линейного кода с порождающей матрицей
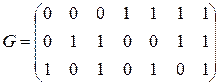
4. На приемном конце канала связи, использующего код Хэмминга  с проверочной матрицей
с проверочной матрицей
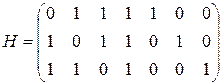 ,
,
было принято слово (1101010). Какое кодовое слово передавалось, если возможно не более одной ошибки?
Занятие 10 (5 часов)
Тема. Криптография.
Цель. Ознакомление с принципами классической и современной криптографии.
Теоретические вопросы. Малая теорема Ферма, функция Эйлера, примитивный элемент конечного поля, дискретный логарифм, система RSA, электронная подпись.
Методические указания. Приступая к данной теме целесообразно сделать небольшой экскурс в историю криптографии и рассказать о значении криптографии в современном обществе. Затем следует напомнить об основных понятиях теории чисел таких как простое число, разложение на простые множители, наименьшее общее кратное, наибольший общий делитель, взаимно простые числа, алгоритм Евклида для нахождения наибольшего общего делителя, функция Эйлера и Малая теорема Ферма. В качестве упражнения можно предложить студентам возвести число а в 53 степень с помощью 8 умножений. Это может быть осуществлено следующим образом
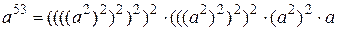 .
.
Задачи.
1. Разложить число п =3552377 на простые множители, если известно, что оно равно произведению двух разных простых чисел и функция Эйлера 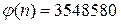 .
.
2. Сообщение
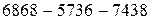
зашифровано по системе RSA с открытым ключом 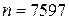 и
и 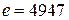 . Кроме того, известно, что
. Кроме того, известно, что 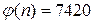 . Требуется расшифровать это сообщение.
. Требуется расшифровать это сообщение.
ЛИТЕРАТУРА
1. Андерсон Д.А. Дискретная математика и комбинаторика. – М.: «Вильямс», 2003.
2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.: «Наука», 2004.
3. Дориченко С.А., Ященко В.В. 25 этюдов в шифрах. – М.: «ТЕИС», 1994.
4. Зуев Ю.А. Лекции по дискретной математике. – М.: МГУТУ, 2004.
5. Иванов Б.Н. Дискретная математика. Алгоритмы и программы. – М.: «Лаборатория базовых знаний», 2002.
 2015-06-28
2015-06-28 992
992







