Аналитическое моделирование

Аналитическое моделирование – математическая формализация, изменение свойств объекта во времени.

Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраические, интегродифференцированные, конечно-разностные) и логических условий.

Аналитическая модель может быть исследована 3-я способами:

1) аналитическим способом – стремятся получить в общем виде зависимость от исходных характеристик;

2) численным способом – когда нельзя решить в общем виде, то получаем результаты для конкретных начальных данных;

3) качественным способом – не имея решения управления в общем виде, мы можем найти некоторые свойства решения.

Аналитические модели удобны в использовании, поскольку для аналитического моделирования не требуются сколько-нибудь значительные затраты вычислительных ресурсов, часто без постановки специальных вычислительных экспериментов исследователь может оценить характер влияния аргументов на выходные параметры, выявить те или иные общие закономерности в поведении системы. Но, к сожалению, аналитическое исследование удаётся реализовать только для частных случаев сравнительно несложных СМО. Для сложных СМО аналитические модели, если и удаётся получить, то только при принятии упрощающих допущений, ставящих под сомнение адекватность модели.

Поэтому основным подходом к анализу САПР на системном уровне проектирования считают имитационное моделирование, а аналитическое исследование используют при предварительной оценке различных предлагаемых вариантов систем.

Некоторые компоненты СМО характеризуются более чем одним входным и/или выходным потоками заявок. Правила выбора одного из возможных направлений движения заявок входят в соответствующие модели компонентов. В одних случаях такие правила относят к исходным данным (например, выбор направления по вероятности), но в некоторых случаях желательно найти оптимальное управление потоками в узлах разветвления. Тогда задача моделирования становится более сложной задачей синтеза, характерными примерами которой являются маршрутизация заявок или синтез расписаний и планов.

2.1 Математическое программирование

Математическое программирование занимается исследованием свойств и разработкой методов решения задач следующего вида: найти значения переменных x = (x ₁, x ₂,..., x_n), принадлежащих некоторому заданному множеству Х и доставляющих максимум (минимум) заданной функции F (x ₁, х ₂,..., x_n) этих переменных. Если для определённости говорить о задаче максимизации, то её краткая запись будет иметь вид max[ F (x)| x Î X ]. Источником такого рода задач является любая область практической деятельности человека и прежде всего производство, распределение, обмен и потребление материальных благ, т. е. сфера экономики.

Характерные особенности современной экономики, такие как усложнение связей и зависимостей между элементами экономических систем на всех уровнях, ускорение темпов внедрения научно-технических достижений в производство, необходимость учёта ограниченности ресурсов при гигантских масштабах производства и капитальных вложений, приводят к одновременному существованию для каждой экономической задачи множества вариантов её решения, существенно различающихся между собой по затратам, срокам исполнения, срокам окупаемости, экономическому, социальному эффекту. Если определены условия, при которых осуществляется выбор решения, и указан критерий, в соответствии с которым будет оцениваться его качество (другими словами, задано множество Х и функция F (x)),то мы получаем сформулированную выше в общем виде задачу математического программирования. В соответствии с принятой в математическом программировании терминологией элементы множества Х называются допустимыми планами (точками, векторами, решениями). Задача математического программирования, для которой существуют допустимые планы, называется допустимой. Функция F (х), подлежащая максимизации (или минимизации), называется целевой. Допустимый план, доставляющий наибольшее (наименьшее) значение целевой функции, называется оптимальным планом (точкой, вектором, решением) задачи.

Множество Х допустимых планов задаётся обычно как множество решений некоторой системы уравнений и (или) неравенств. Система уравнений и неравенств, определяющих множество X, называется системой ограничений (условий) задачи, а каждое из уравнений или неравенств – ограничением (условием) задачи. В конкретных исследованиях ограничения отражают условия, в которых происходит выбор решения.

В зависимости от особенностей целевой функции и функций, задающих ограничения, задачи математического программирования разделяются на ряд классов.

Задачи линейного программирования возникают, если все соотношения в их формулировке линейны: целевая функция – линейная форма z = cx= c ₁ x ₁ + c ₂ x ₂ c_ix_i +... + c_nx_n переменных х ₁, х ₂, ..., х_n, ограничения – линейные равенства и неравенства, задающие выпуклое многогранное множество. Различия в свойствах этого множества, определяемые особенностями системы ограничений, приводят к тому, что среди задач линейного программирования выделяются частные постановки: транспортная, распределительная, блочная и другие задачи.

Задачи нелинейного программирования – такие задачи, в постановке которых нелинейна хотя бы одна из функций. Если о свойствах функций ничего более не сообщается, задача является общей задачей нелинейного программирования. Если же известно, что ограничения задают выпуклую область, на которой ищется максимум целевой функции, выпуклой вверх, или минимум функции, выпуклой вниз, – получаем задачу выпуклого программирования. Частным случаем задачи выпуклого программирования является задача квадратичного программирования. В ней множество допустимых решений задаётся линейными ограничениями и представляет, следовательно, выпуклое многогранное множество, а целевая функция – квадратичная форма, неположительно определённая для задач максимизации и неотрицательно определённая для задач минимизации.

Задачи целочисленного программирования – это те задачи математического программирования, в постановке которых присутствует требование целочисленности всех или части переменных (соответственно полностью или частично целочисленные задачи). Таким образом, можно говорить о целочисленных задачах нелинейного, выпуклого, линейного программирования. Они, в свою очередь, являются частным случаем более широкого класса задач дискретного программирования, которое охватывает задачи, определённые на конечных множествах допустимых решений.

При рассмотрении задач математического программирования различают два этапа: постановку задачи и её решение. Математика исследует не реальные объекты и отношения, а их абстракции. Одной из таких абстракций является математическая модель –формальное описание изучаемого явления, отражающее его наиболее существенные для данного конкретного случая черты. К модели предъявляются противоречивые требования: с одной стороны, она должна быть по возможности простой, а с другой – достаточно точной. Вопрос о том, что значит «по возможности» и «достаточно» обычно решается вне рамок математического программирования.

2.1.1 Линейное программирование

Линейное программирование (ЛП) представляет собой математическую теорию нахождения экстремума линейной целевой функции нескольких переменных при действии связывающих их линейных ограничений.

Математически задача ЛП ставится следующим образом: ищется максимум (минимум) линейной формы (функции цели):

(1)

при условиях:

a_i ₁ x ₁ + a_i ₂ x ₂ + a_inx_n ≤ b_i; x ≥ 0;(2)

i = 1,2, ..., m; m > n.

Векторная форма записи задачи ЛП имеет вид:

найти max f (X) = Z = C·X (3)

при ограничениях А ₁ х ₁ + А ₂ х ₂ + …+ А_nx_n = B, x ≥ 0,

где С = (с ₁, c ₂, ..., c_n), X = (x ₁, x ₂, ..., x_n).

Постановка задачи управления запасами лесоматериалов в такой форме имеет место при возможности линейного представления зависимостей между основными факторами.

2.1.2 Динамическое программирование (ДП)

ДП есть особый математический метод оптимизации решений, специально приспособленный к многошаговым (или многоэтапным) операциям.

Рассмотрим операцию, распадающуюся на ряд последовательных «шагов» или «этапов», например, управление запасами лесоматериалов на последовательных периодах осуществления ЛЗП. Пусть эффективность операции характеризуется показателем W, называемым «выигрышем», складывающимся из выигрышей на отдельных шагах:

; , (4)

где w_i – выигрыш на i -м шаге.

Если W обладает таким свойством, то его называют «аддитивным критерием».

Операция представляет собой управляемый процесс, т. е. мы можем выбирать какие-то параметры, влияющие на его ход и исход, причём на каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш за операцию в целом. Будем называть это решение «шаговым управлением». Совокупность всех шаговых управлений представляет собой управление операцией в целом. Обозначим его буквой u, а шаговые управления – буквами u ₁, u ₂, u ₃, … u_m:

. (5)

При этом u ₁, u ₂, … u_m в общем случае не числа, а, может быть, векторы, функции и т. д. Требуется найти такое управление u, при котором выигрыш W обращается в max:

. (6)

То управление u *, при котором этот max достигается, будем называть оптимальным управлением. Оно состоит из совокупности оптимальных шаговых управлений:

.

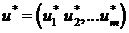Тот максимальный выигрыш, который достигается при этом управлении, будем обозначать W ^*:

(7)

Рассмотрим пример многошаговых операций применительно к ЛЗП, а именно задачу об управлении запасами. Например, требуется обосновать вместимость склада под сезонный запас хлыстов с учётом сезонной неравномерности вывозки. Годовой период работы лесозаготовительного предприятия делится на этапы: зимний период, весеннюю распутицу, летний период, осеннюю распутицу. Оптимальным будет вариант, при котором суммарные денежные издержки по созданию запасов и из-за простоев оборудования вследствие преждевременного расхода запаса будут наименьшими. В основе метода ДП лежит идея постепенной, пошаговой оптимизации. При этом управление на каждом шаге должно выбираться с учётом всех его будущих последствий на ещё предстоящих шагах. Управление на i -м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей на всех оставшихся до конца шагах плюс данный шаг. Поэтому процесс ДП обычно разворачивается от конца к началу. Прежде всего планируется последний, m -й шаг. Планируя последний шаг, нужно сделать разные предположения о том, чем кончился предпоследний (m – 1)-й шаг для каждого предположения, найти условное обозначение управления на m -м шаге. Аналогичным образом, «пятясь назад», находятся все условные оптимальные управления и условные оптимальные выигрыши на всех шагах, начиная от данного и до конца. Теперь можно построить уже не условно оптимальное, а просто оптимальное управление u * и найти оптимальный выигрыш W *.

Метод ДП является очень мощным и плодотворным методом оптимизации управления. Но это решение не сводится к какой-либо стандартной вычислительной процедуре; оно может быть передано на компьютер только после того, как составлены соответствующие алгоритм и реализующие его зависимости и формулы.

В основе решения всех задач ДП лежит «принцип оптимальности»: «Каково бы ни было состояние системы S перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным».

Постановку задачи ДП удобно проводить в следующем порядке.

1. Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.

2. Расчленить операцию на этапы (шаги).

3. Выяснить набор шаговых управлений u_i для каждого шага u налагаемые на них ограничения.

4. Определить, какой выигрыш приносит на i -ом шаге управление u_i, если перед этим система была в состоянии S, т. е. записать «функции выигрыша»:

. (8)

5. Определить, как изменится состояние S системы S под влиянием управления u_i на i -ом шаге: оно переходит в новое состояние

. (9)

6. Записать основное рекуррентное управление ДП, выражающее условный оптимальный выигрыш W_i (S) через уже известную функцию W_i ₊₁(S):

(10)

7. Произвести условную оптимизацию шагов, начиная с последнего.

8. Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге.

2.1.3 Теория массового обслуживания (ТМО)

Очень многие технологические процессы ЛЗП можно рассматривать как системы массового обслуживания (далее СМО). Любую СМО в общем виде можно представить как совокупность последовательно связанных между собой входящих потоков требований на обслуживание, очередей, каналов обслуживания и выходящих потоков. Случайный характер входящего потока требований (хлыстов, сортиментов, автолесовозов и т. д.), а также длительности обслуживания каналом (раскряжёвочная установка, лесопильная рама, краны и т. д.) приводит к образованию случайного процесса в системе, который необходимо исследовать.

Предметом ТМО является установление зависимости между условиями работы СМО (число каналов, их производительность, характер потока заявок, правила обслуживания) и эффективностью обслуживания. В качестве показателей эффективности обслуживания могут применяться: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания; среднее время простоя отдельных каналов и системы в целом, закон распределения длины очереди и др.

Каждый из этих показателей характеризует степень приспособленности системы к обслуживанию потока заявок, т. е. пропускную способность. Различают абсолютную и относительную пропускную способность. Под абсолютной пропускной способностью понимают среднее число заявок, которое СМО может обслужить в единицу времени. Под относительной пропускной способностью понимают среднее отношение числа обслуженных заявок к числу поданных.

СМО по наличию того или иного признака можно разделить следующим образом:

1. По характеру поступления требований – на системы с регулярными и случайными потоками поступления требований в систему. Если количество поступающих требований в систему в единицу времени (интенсивность потока) постоянно или является заданной функцией времени, то имеем систему с регулярным потоком поступления требований в систему, в противном случае – со случайным. Для исследования СМО со случайным потоком требований необходимо, чтобы была задана или известна функция распределения вероятностей поступления требований в систему. Если параметры потока требований не зависят от расположения рассматриваемого интервала времени на оси времени, то имеем стационарный поток требований, в противном случае – нестационарный. Например, если число лесовозов, приходящих на склад, не зависит от времени суток, то поток требований – стационарный.

2. По количеству поступающих требований в один момент времени на системы с ординарным и неординарным потоками требований. Если вероятность поступления двух или более требований в один момент равна нулю или имеет столь малую вероятность, что ею можно пренебречь, то имеем систему с ординарным потоком требований.

3. По связи между требованиями на системы без последействия и с последействием. Если вероятность поступления требований в систему в некоторый момент времени не зависит от того, сколько уже требований поступило в систему, т. е. не зависит от предыстории изучаемого процесса, то мы имеем систему без последействия, в противном случае – с последействием.

4. По характеру поведения требования в системе – с отказами, с ограниченным ожиданием и с ожиданием без ограничения:

- если вновь наступившее на обслуживание требование застаёт все каналы обслуживания занятыми и оно покидает систему, то имеем систему с отказами;

- если поступившее требование застаёт все каналы обслуживания занятыми и становится в очередь, но находится в ней ограниченное время, после чего, не дождавшись обслуживания, покидает систему, то имеем систему с ограниченным ожиданием;

- если поступившее требование, застав все каналы занятыми, вынуждено ожидать своей очереди до тех пор, пока оно не будет обслужено, то имеем систему с ожиданием без ограничения.

5. По способу выбора требований на обслуживание: с приоритетом, по мере поступления (FIFO), случайно, последний обслуживается первым (LIFO). В этом случае говорят о дисциплине обслуживания:

- если СМО охватывает несколько категорий требований и по каким-либо соображениям необходимо соблюдать различный подход к их отбору, то имеем систему с приоритетом;

- если освободившийся канал обслуживает требование, ранее других поступившее в систему, то имеем систему с обслуживанием требований по мере их поступления (FIFO);

- если требования из очереди в канал обследования поступают в случайном порядке, то имеем систему со случайным выбором требований на обслуживание;

- последний обслуживается первым – LIFO (пример: разборка штабелей лесоматериалов).

6. По характеру обслуживания требований – на системы с детерминированным и случайным временем обслуживания. Если интервал времени между моментом поступления требования в канал обслуживания и моментом выхода требования из этого канала постоянен, то имеем систему с детерминированным временем обслуживания, в противном случае – со случайным.

7. По числу каналов обслуживания – на одноканальные и многоканальные.

8. По количеству этапов обслуживания – на однофазные и многофазные системы. Если каналы обслуживания расположены последовательно и они неоднородны, т. к. выполняют различные операции обслуживания, то имеем многофазную СМО.

9. По однородности требований, поступающих на обслуживание, – на системы с однородными и неоднородными потоками требований. Так, если под разгрузку прибывают автомобили различной грузоподъёмности, то такие требования называются неоднородными, если одной грузоподъёмности – однородными.

10. По ограниченности потока требований – на замкнутые и разомкнутые системы. Если поток требований ограничен и требования, покинувшие систему, могут в неё возвращаться, то имеем замкнутую систему, в противном случае – разомкнутую.

Поток требований, обладающий тремя свойствами: стационарностью, ординарностью и отсутствием последействия, называется простейшим (или стационарным пуассоновским) потоком.

На лесозаготовках встречаются все основные типы СМО.

Важной особенностью функционирования СМО является взаимодействие очередей. Последнее может возникнуть при одновременном обслуживании нескольких потоков и наличии «узких» мест в системе обслуживания. Например, один кран на нижнем лесоскладе нередко одновременно обслуживает 3 потока: выполняет погрузку лесоматериалов в вагоны, обслуживает основные технологические линии и лесообрабатывающие цехи.

Математический анализ работы СМО очень облегчается, если процесс этой работы – марковский. Для этого достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние, были простейшими. Случайный процесс, протекающий в системе, называется марковским, если для любого момента времени 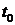вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент 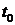и не зависят от того, когда и как система пришла в это состояние.

При оптимизации практических задач большое значение имеют так называемые марковские случайные процессы с дискретными состояниями и непрерывным временем.

Процесс называется процессом с дискретными состояниями, если его возможные состояния можно заранее перечислить (перенумеровать), а переход системы из состояния в состояние происходит «скачком», практически мгновенно.

Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а неопределённы, случайны, если переход может осуществиться, в принципе, в любой момент.

При анализе случайных процессов с дискретными состояниями удобно пользоваться графом состояний, связывающим все возможные состояния системы. В случае, если на графе состояний представлены интенсивности потоков событий, переводящих систему из состояния в состояние, граф называется размеченным.

Решение задачи методами аналитического аппарата ТМО проводится по следующей схеме:

1. Разрабатывается граф состояний СМО, изображающий состояния системы и связывающие их возможные переходы.

2. Составляется система дифференциальных уравнений состояний СМО.

3. В случаях необходимости определения предельных установившихся (так называемых финальных) вероятностей состояний система дифференциальных уравнений Колмогорова сводится к системе линейных алгебраических уравнений посредством устремления .

4. Находят значения интересующих показателей функционирования СМО.

С точки зрения задач управления запасами лесоматериалов особый интерес представляют три расчётные схемы: одноканальная и многоканальная СМО с ограничением по длине очереди и многофазные СМО.

Схема 1. Рассмотрим одноканальную СМО с ограничением по длине очереди. Такая расчётная схема соответствует работе большинства машин в ЛЗП со случайными временем поступления и параметрами заготовок, случайной продолжительностью обслуживания и выдачи обработанных лесоматериалов.

На одноканальную СМО поступает простейший поток заявок с интенсивностью l, время обслуживания показательное с параметром . В очереди m мест. Если заявка приходит в момент, когда все эти места заняты, она получает отказ и покидает СМО.

Решение:

Состояния СМО:

S ₀ – СМО свободна;

S ₁ – канал занят, очереди нет;

S ₂ – канал занят, одна заявка в очереди;

…………………………………………..

S_k – канал занят, (k – 1) заявок в очереди;

...................................................................

S_m ₊₁ – канал занят, m заявок в очереди.

Схема 2. Рассмотрим многоканальную СМО с ограничением по длине очереди. Такая расчётная схема соответствует одновременной работе нескольких однотипных машин на одной технологической операции или в связанной совокупности последовательно выполняемых ими операций.

Расчётная схема выглядит следующим образом. На n -канальную СМО с ожиданием поступает поток заявок с интенсивностью ; интенсивность обслуживания (для одного канала) – , число m мест в очереди ограничено. Финальные вероятности состояний существуют при любых .

Решение:

Состояния СМО нумеруются по числу заявок в системе:

S ₀ – все каналы свободны;

S ₁ – занят один канал;

…………………………………………..

S_k – занято k каналов ;

…………………………………………..

S_n – заняты все n каналов;

S_n ₊₁ – заняты все n каналов, 1 заявка стоит в очереди;

…………………………………………..

S_n ₊ _r – заняты все n каналов, r заявок стоят в очереди.

Схема 3. Рассмотрим несколько СМО с ожиданием, последовательно соединённых друг с другом так, что поток обслуженных требований, выходящий из одной системы, является потоком, входящим в следующую систему. Такое соединение систем принято называть многофазной СМО с ожиданием. Каждая составляющая системы называется фазой. Входящим потоком требований для многофазной СМО является поток, входящий в первую фазу; выходящим потоком – выходящий из последней фазы. Введём обозначения: r – число фаз; N_j – число узлов обслуживания в j -й фазе;μ _j – интенсивность обслуживания для узла j -й фазы (1 ≤ j ≤ r); λ – параметр входящего пуассоновского потока.

Такая расчётная схема соответствует одновременной работе разнородных машин или установок в составе систем машин или технологических линий ЛЗП. Установившийся режим работы многофазной СМО существует только в предположении, что:

α _j < N_j (11)

1 ≤ j ≤ r.

При соблюдении условия (11) вероятность того, что в j -й фазе находится n требований (сколько требований находится при этом в других фазах – безразлично) совпадает с формулой, которая определяет характеристики СМО с ожиданием, имеющей один узел обслуживания. Таким образом, вероятность состояния одной выделенной фазы в многофазной системе совпадает с вероятностью состояния одной фазы, рассматриваемой как отдельная СМО.

Следовательно, остальные характеристики отдельной СМО также окажутся характеристиками фазы в многофазной СМО. Многие характеристики многофазной СМО получаются суммированием соответствующих характеристик по фазам. К ним относятся, например, среднее число требований, находящихся в очередях, среднее время ожидания и другие (но не вероятность наличия очереди хотя бы в одной фазе).

Возможности аналитического моделирования значительно ограничены в силу необходимости представления эмпирических зависимостей теоретическими законами и наличия существенных ограничений, накладываемых на условия и параметры реальных систем и моделируемых ситуаций. Имитационное и нейронечёткое моделирование в значительной степени свободны от статичности идеализации эмпирических распределений теоретическими законами.