Для определения диапазона регулирования частот вращения (Dv) необходимо предварительно выяснить значения наибольшей и наименьшей частоты вращения шпинделя 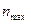 и
и 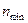 ).
).
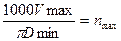 ,
, 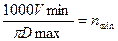 ,
,
где Vmax, Vmin и Dmax, Dmin  — соответственно предельные скорости резания, м/мин и диаметры обрабатываемых деталей, мм.
— соответственно предельные скорости резания, м/мин и диаметры обрабатываемых деталей, мм.
Зная 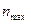 и
и 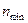 , получим значение Dv
, получим значение Dv
Dv = 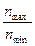
Учитывая совершенствование режущего инструмента, форсирование при этом режимов резания увеличивают на 15—20% полученное значение 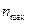 , что, естественно, приводит к такому же увеличению и Dv, - диапазона регулирования частот вращения.
, что, естественно, приводит к такому же увеличению и Dv, - диапазона регулирования частот вращения.
Для получения оптимальных режимов резания во всем диапазоне обрабатываемых размеров предпочтительнее осуществить бесступенчатое регулирование частот вращения и подач. Однако такое решение не всегда является экономически целесообразным. В этом случае выбирают вариант ступенчатого регулирования. Распределение частот вращения шпинделя (скоростей подач) принимают по геометрической прогрессии со следующими стандартными значениями знаменателя j.
j =1,06,j =1,12; j =1,26, j =1,41; j =1,58; j =|1,78; j =2.
В станкоинструментальных нормативных документах принято применять ряды скоростей со следующими значениями знаменателей:
1) для крупных станков общего назначения и станков с настройкой кинематической цепи привода сменными зубчатыми колесами j = 1,26; j =1.12;
2) для средних токарных j = 1,26, -1,58
3) для токарно-револьверных j = 1,26, -1,58
4) для токарных одношпиндельных автоматов j = 1,26, -1,12
5) для токарных многошпиндельных автоматов и полуавтоматов j = 1,26, -1,12
6) для токарно - карусельных j = 1,26, -1,41
7) для вертикально - сверлильных j = 1,41, -1,78
8) для радиально - сверлильных j = 1,26, -1,12
9) для фрезерных и продольно - фрезерных j = 1,41, -1,26
10) для расточных j = 1,26, -1,58
После выбора требуемого значения j необходимо откорректировать полученные после увеличения на 15-20% Dv значения Nmax и Nmin, приведя их в соответствие с рядом чисел регламентированных стандартом на нормальные ряды чисел в станкостроении, приведенным в приложениях настоящего методического пособия.
Число ступеней Z частот вращения (скоростей) проектируемого привода
определяется по формуле
Z = 1 + 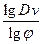

Полученное значение округляется до целого таким образом, чтобы его можно было разложить на простые множители 2 и 3. Рекомендуемые значения Z = 2,3,4, 6,8, 9,12,16, 18,24, 27, 32 и т. д.
Выделенные полужирным шрифтом — наиболее часто применяемые значения j. и Z.
Записываем, в соответствии со стандартом, нормальный ряд частот вращения, соответствующий выбранному j, по количеству частот равный принятому значению Z, и приступаем к разработке кинематической схемы коробки скоростей.
Задача сводится к определению количества валов, расположению по валам пар зубчатых колес и количества зубьев у каждого колеса. При Z = 4 коробка может иметь два вала. Она будет компактна, если мы разместим на одном валу четверной или два двойных блока с поочередным включением последних. Такая конструкция требует наличия блокировочного устройства, не позволяющего одновременно включать эти блоки.
Для Z. >4, т. е. для многоваловой коробки, необходимо решить вопрос о распределении скоростей по валам. Принимаем Z, = P 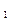 P
P 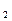 P
P 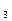 .....P
.....P 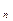 , при этом желательно, чтобы количество передач в группах уменьшалось по ходу кинематической цепи от первого вала к последнему, т.е, чтобы.P
, при этом желательно, чтобы количество передач в группах уменьшалось по ходу кинематической цепи от первого вала к последнему, т.е, чтобы.P 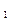 > P
> P 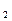 > P
> P 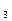 >..... > P
>..... > P 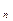 ,
,  где Р — количество передач в каждой группе; n — число групп. Это пожелание носит рекомендательный характер и при соответствующей серьезной аргументации может быть нарушено конструктором.
где Р — количество передач в каждой группе; n — число групп. Это пожелание носит рекомендательный характер и при соответствующей серьезной аргументации может быть нарушено конструктором.
Для примера разберем случай соответствующий Z =12
Z = 3 х 2 х 2 = 12, n =3. Эту задачу можно решать двумя способами: аналитическим и графоаналитическим. Предпочтение отдают графоаналитическому, так как он обладает большей наглядностью и позволяет быстрее найти оптимальный вариант решения.
При этом методе последовательно строят возможные варианты структурных сеток, анализируют их по трем признакам, выбирают оптимальный, по нему строят график чисел оборотов шпинделя, по графику чисел оборотов определяют передаточные отношения передач в группах и числа зубьев колес в них входящие..
Для построения структурной сетки проводят горизонтальные линии, которые условно обозначают валы в коробке. Число этих линий в нашем примере будет равно n +1, т.е.—четыре. Затем на равном расстоянии друг от друга проводим вертикальные линии, по количеству соответствующие числу Z регулируемых частот вращения шпинделя (Z = 12).Считаем, что расстояние между ними соответствует lgj. Построение структурной сетки начнем с точки «О», находящейся на середине 1 вала. Из этой точки проведем лучи, соответствующие числу передач первой группы, т. е. между I и II валом — три передачи, между II, III и между III и IV—по две передачи. Лучи, идущие от 0 вправо, будут соответствовать повышающим передачам, влево — понижающим, а вертикально вниз, - равным единице. Расстояние между концами лучей, выраженное через lgj. будет соответствовать характеристике группы. Структурные сетки обязательно симметричны.
Характеристика группы равна числу ступеней скорости совокупности групповых передач, кинематически предшествующих данной группе (равна количеству передач, кинематически предшествующих данной группе, т.е. 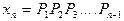 ).
).
Для последовательного получения всех частот вращении шпинделя сначала переключают передачи основной группы, затем первой переборной, второй и т. д. В нашем случае Z = P 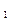 P
P 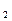 P
P 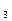 = 3 х 2 х 2 = 12. Примем, что группа P
= 3 х 2 х 2 = 12. Примем, что группа P 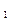 — основная; P
— основная; P 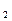 — первая переборная; Рз— вторая переборная. Для основной группы передач характеристика Хо всегда равняется единице; для первой переборной Х
— первая переборная; Рз— вторая переборная. Для основной группы передач характеристика Хо всегда равняется единице; для первой переборной Х 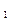 = P
= P 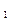 =3, для второй Х
=3, для второй Х 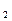 = P
= P 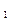 P
P 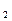 =3 х 2 = 6, где P
=3 х 2 = 6, где P 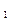 и P
и P 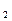 — количество передач в основной и первой переборной группах. В этом случае наша структурная формула примет вид:
— количество передач в основной и первой переборной группах. В этом случае наша структурная формула примет вид:
Z = 12 = 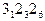
Основной и различными по номеру переборными группами может быть принята проектировщиком любая из групп передач в приводе, поэтому наряду с конструктивными вариантами привода (Z = 3х2х2 = 2х3х2 = 2х2х3 = 4х3 = 3х4) необходимо рассматривать и кинематические варианты, т.е. возможные варианты нумерации основных и переборных групп. Для нашего примера рассмотрим лишь шесть вариантов структур (рис. 1), полагая заранее, что выбор конструктивных вариантов 4х3 или 3х4 приведет к необоснованному увеличению осевых габаритов коробки скоростей.
Построив возможные для Z = 12 структурные сетки, переходят к их анализу для определения оптимального варианта, учитывая при этом следующие рекомендации и ограничения.
Во избежание чрезмерно больших диаметров колес, а также в целях нормальной их работы практикой установлены следующие предельные передаточные отношения между валами для прямозубого зацепления:
в коробках скоростей 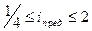
в коробках подач 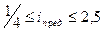
Отсюда наибольший диапазон регулирования групповой передачи будет
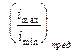
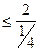
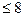
Отношение 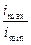 имеет наибольшую величину для последней переборной группы привода. Следовательно, для коробок скоростей
имеет наибольшую величину для последней переборной группы привода. Следовательно, для коробок скоростей
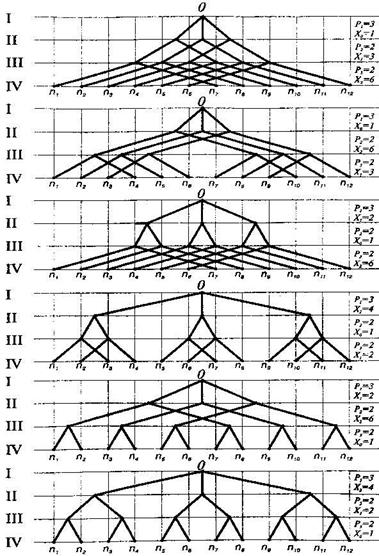
Рис.1. Варианты структурных сеток для Z = 12
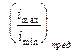 =
= 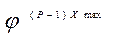 = 8
= 8
где 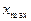 - наибольший показатель для последней переборной группы (
- наибольший показатель для последней переборной группы (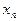 );
);
Р — число передач в этой же группе.
Используя формулу (5), а также желательность выполнения следующих неравенств P 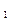 > >P
> >P 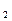 :>P
:>P 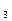 >..... > P
>..... > P 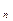 и Х
и Х 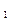 < Х
< Х 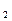 < Х
< Х 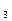 <.....< Х
<.....< Х 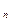 анализируют все возможные варианты структурных сеток. В нашем примере, - шесть возможных вариантов, проанализировав которые с использованием выше приведенных зависимостей и неравенств мы, придем к выводу, что наиболее рациональным является первый вариант, который и определит структуру проектируемого привода..
анализируют все возможные варианты структурных сеток. В нашем примере, - шесть возможных вариантов, проанализировав которые с использованием выше приведенных зависимостей и неравенств мы, придем к выводу, что наиболее рациональным является первый вариант, который и определит структуру проектируемого привода..
При большом диапазоне регулирования может возникнуть ситуация когда ни одна из возможных множительных структур не удовлетворяет условиям уравнения (5) из-за большого значения характеристики последней переборной группы В этом случае рекомендуется от множительных структур перейти к сложенным и рассматривать их с целью выбора оптимального варианта
После этого переходят к построению графика частоты вращения шпинделя. Для этого на равном расстоянии друг от друга проводят горизонтальные линии, число которых равно числу валов коробки. Затем, с интервалами равными выбранному ранее значению j, проводят вертикальные линии, по количеству соответствующие выбранному числу Z ступеней вращения шпинделя или подачи. При построении графика частот вращения учитывается особенность отдельных передач и предельные значения передаточных отношений в группах.
График частот вращения начинают строить с первого вала, используя выбранный оптимальный вариант структурной сетки. Поле каждой группы структурной сетки накладывают на соответствующее поле графика частоты вращения так, чтобы расстояния между концами лучей и их количество в группе сохранялись такими же, как на структурной сетке. Условие симметричности при построении графика частот вращения не соблюдается (рис. 2).
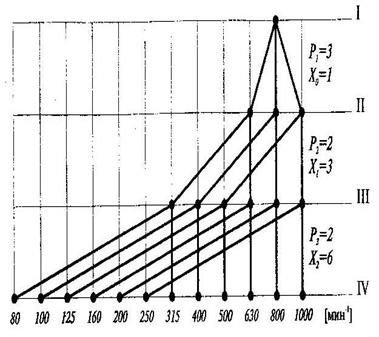
Рис. 2. График частот вращения шпинделя (вал IV) для Z=12
Для улучшения динамики привода следует стремиться, чтобы частота вращения входного вала I, была близка к максимальной на выходном (последнем) валу. Наиболее целесообразно при этом построить кинематическую цепь так, чтобы сохранить более высокими частоты вращения промежуточных валов. В этом случае, к роме прочего, уменьшаются и габариты коробки скоростей. В этих же целях, а так же для улучшения технологичности проектируемого привода, необходимо стремиться к тому, что хотя бы одна пара колес в групповой передаче имела передаточное отношение равное единице (вертикальный луч), а остальные передачи были бы симметричны, т.е. 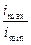 = 1.В случае невозможности выполнения обеих рекомендаций предпочтение отдают первой. При этом надо иметь в виду, что они носят лишь рекомендательный характер и в ряде случаев, при наличии серьезных оснований, конструктор может не выполнить ни одно из них.
= 1.В случае невозможности выполнения обеих рекомендаций предпочтение отдают первой. При этом надо иметь в виду, что они носят лишь рекомендательный характер и в ряде случаев, при наличии серьезных оснований, конструктор может не выполнить ни одно из них.
Иногда возникает необходимость корректировки графика частот, связанная с отличием полученного диапазона регулирования от заданного в техническом задании либо полученного расчетом по уравнению (1) после увеличения его на 15-20 %. В этом случае применяют один из следующих способов изменения диапазона:
1) с перекрытием ряда ступеней частот вращения (произвольное изменение характеристики последней переборной группы);
2) с ломаным рядом частот (произвольное изменение характеристики основной группы).
Построенный график (см. рис. 2), с указанными значениями частот вращения шпинделя (для рассматриваемого нами примера) позволяет определить передаточные отношения всех передач. Для передач изображенных на графике вертикальным лучом передаточное отношение равняется единице (i =  ), для передач, соответствующих лучам отклоненным вправо, передаточное отношение будет иметь значение j в степени, равной количеству интервалов на сколько луч отклонился вправо от начальной точки. Для передач, изображенных лучами отклоняющимися влево передаточное отношение рассчитывается аналогично предыдущему, но показатель степени будет иметь отрицательное значение.
), для передач, соответствующих лучам отклоненным вправо, передаточное отношение будет иметь значение j в степени, равной количеству интервалов на сколько луч отклонился вправо от начальной точки. Для передач, изображенных лучами отклоняющимися влево передаточное отношение рассчитывается аналогично предыдущему, но показатель степени будет иметь отрицательное значение.
В соответствии с графиком строится кинематическая схема с учетом количества передач в каждой группе (рис. 3).
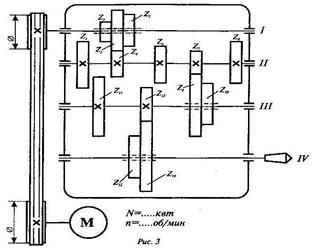
Кинематическая схема с числом ступеней регулирования Z=12
По найденным передаточным отношениям определяют числа зубьев колес в каждой группе и каждой передаче.
Следует помнить, что сумма чисел зубьев сопряженных колес, числа зубьев червячных колес и модули зубчатых колес стандартизованы. При неизменном межосевом расстоянии и одинаковом модуле сумма чисел зубьев каждой пары является величиной постоянной.
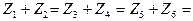 ...
... 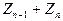 = const
= const
Рис. 3. Кинематическая схема коробки скоростей
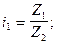
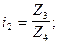
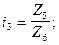 ........
........ 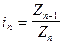
Из уравнений (6) и (7) следует
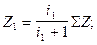
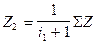
По принятой сумме зубьев, а ее рекомендуется выбирать конструктору из интервала 80 - 120, находят числа зубьев колес группы. При этом необходимо, чтобы у каждого из колес проектируемого привода было не менее 20—22 зубьев.
В случае неравенства модулей колес в группе, что крайне нежелательно, расчет чисел зубьев проводят из условия постоянства межосевого расстояния.
При расчете числа зубьев рекомендуется пользоваться методикой, изложенной на стр. 366 [3], или принимать их из [4].
Полученные числа зубьев наносим на кинематическую схему рядом с изображением соответствующего колеса.
 2017-10-25
2017-10-25 3856
3856
