Оценка качества эконометрических регрессионных моделей по адекватности

Качества линейных эконометрических уравнений регрессии оценивается стандартным для эконометрики - математическим образом по адекватности и точности.

Под адекватностью понимается соответствие модели изучаемому процессу или явлению. Т.к.полного соответствия между ними быть не может, то адекватность в какой-то мере условное понятие. При моделировании имеется в виду адекватность не вообще, а по тем свойствам, которые считаются существенными для модели.

Регрессионная модель у^*_t некоторого временного ряда у_t считается адекватной, если правильно отражает систематические компоненты временного ряда.

Случайность колебаний уровней остаточной последовательности, в соответствии случайной компоненты нормальному закону, равенства мат.ожидания случайной компоненты =0 и независимость значений уравнений случайной компоненты.

Проверка случайности колебаний уровней остаточной последовательности означает проверку гипотезы о правильности выбора вида тренда. Для исследования случайности отклонений от тренда необходимо рассмотреть набор разностей

(t = 1, 2, …, n)

Характер этих отклонений изучается с помощью ряда непараметрических критериев.

1) Одним из таких критериев является критерий серий, основанный на медиане выборки. Ряд из величин ε_t располагают в порядке возрастания их значений и находят медиану ε_m полученного вариационного ряда, т.е. срединное значение при нечетном n или среднюю арифметическую из двух срединных значений при n четном. Возвращаясь к исходной последовательности ε_tи сравнивая значения этой последовательности с ε_m, будем ставить знак «плюс», если значение ε_t, превосходит медиану, и знак «минус», если оно меньше медианы; в случае равенства сравниваемых величин соответствующее значение ε_t опускается.

Таким образом, получается последовательность, состоящая из плюсов и минусов, общее число которых не превосходит n. Последовательность подряд идущих плюсов или минусов называется серией. Для того чтобы последовательность ε_t была случайной выборкой, протяженность самой длинной серии не должна быть слишком большой, а общее число серий - слишком малым.

Протяженность самой длинной серии обозначается через K_max, а общее число серий - через ν. Выборка признается случайной, если выполняются следующие неравенства для 5%-ного уровня значимости:

;

где квадратные скобки означают целую часть числа.

Если хотя бы одно из этих неравенств нарушается, то гипотеза о случайном характере отклонений уровней временного ряда от тренда отвергается и, следовательно, трендовая модель признается неадекватной.

2) Проверка соответствия распределения случайной компоненты нормальному закону распределения может быть произведена лишь приближенно с помощью исследования показателей асимметрии (γ₁) и эксцесса (γ₂),так как временные ряды, как правило, не очень велики. При нормальном распределении показатели асимметрии и эксцесса некоторой генеральной совокупности равны нулю. Мы предполагаем, что отклонения от тренда представляют собой выборку из генеральной совокупности, поэтому можно определить только выборочные характеристики асимметрии и эксцесса и их ошибки:

; ;

В этих формулах - выборочная характеристика асимметрии; - выборочная характеристика эксцесса; и - соответствующие среднеквадратические ошибки.

Если одновременно выполняются следующие неравенства:

; ,

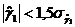то гипотеза о нормальном характере распределения случайной компоненты принимается.

Если выполняется хотя бы одно из неравенств

; ,

то гипотеза о нормальном характере распределения отвергается, трендовая модель признается неадекватной. Другие случаи требуют дополнительной проверки с помощью более сложных критериев.

Кроме рассмотренного метода известен ряд других методов проверки нормальности закона распределения случайной величины: метод Вестергарда, RS-критерий и т. д.

Проверка равенства математического ожидания случайной компоненты нулю, если она распределена по нормальному закону, осуществляется на основе t-критерия Стьюдента. Расчетное значение этого критерия задается формулой

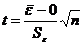где - среднее арифметическое значение уровней остаточной последовательности ε_t;

- стандартное (среднеквадратическое) отклонение для этой последовательности.

Если расчетное значение t меньше табличного значения t_α статистики Стьюдента с заданным уровнем значимости α и числом степеней свободы n -1, то гипотеза о равенстве нулю математического ожидания случайной последовательности принимается; в противном случае эта гипотеза отвергается и модель считается неадекватной.

Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной автокорреляции в остаточной последовательности может осуществляться по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина—Уотсона. Расчетное значение этого критерия определяется по формуле

Расчетное значение критерия Дарбина-Уотсона в интервале от 2 до 4 свидетельствует об отрицательной связи; в этом случае его надо преобразовать по формуле и в дальнейшем использовать значение .

Расчетное значение критерия d (или d') сравнивается с верхним d ₂ и нижним d ₁ критическими значениями статистики Дарбина-Уотсона.

Вывод об адекватности трендовой модели делается, если все указанные выше четыре проверки свойств остаточной последовательности дают положительный результат.

№ 10. Оценка качества эконометрических регрессионных моделей на точность.

Точность модели характеризуется величиной отклонения выхода модели от реального значения моделируемой переменной. При этом в качестве стат. показателей точности применяются следующие: среднее квадратическое отклонение:

σ =√ 1/n-k ∑ (y_t-y_t*)²

средняя относительная ошибка апроксимации;

ε_отн.=1/n Σ y_t-y_t* / y_t*100; %

коэффициент сходимости;

φ²=Σ (y_t-y_t*)² / Σ (y_t – y) ²

коэффициент детерминации;

R²=1-φ²

и др. показатели, где

n-количество уровней ряда;

k-число определенной параметром модели;

y_t*-оценка уровней ряда по модели;

y – среднее арифметическое значение уровней ряда.

На основании указанных показателей можно сделать вывод из нескольких адекватных регрессионных моделей, наиболее точной.

Одним из критериев проверки гипотезы о правильности выбора вида принятой зависимости в регрессионной модели явл. критерий пиков (поворотных точек). Уровень последовательности ε_t считается максимальным, если он больше двух, рядом стоящих уровней, т.е. ε_t ˃ ε_t_-1 и

ε_t ˃ ε_t_+1.

Уровень последовательности ε_t считается минимальным, ели он меньше обоих соседних уровней ε_t ˃ ε_t_-1 и ε_t ˃ ε_t_+1.

В обоих случаях ε_t считается поворотной точкой; общее число поворотных точек для ост-й последовательности ε_t обозначается через p; в случайной выборке мат. ожидания числа точек поворота p и дисперсия σ_p² выражается формулами:

1) p = 2/3 * (n-2);

2) σ_p²=16n-29 / 90.

Критерием случайности с 5–ти %-м уровнем значимости, т.е. с доверительной вероятностью 95% является выполнение неравенства:

p ˃ [ p-1,96* √σ_p²], где [ ] – символизирует целую часть числа; если это неравенство не выполняется, то трендовая модель считается неадекватной.

О качестве модели регрессии можно судить также по значениям коэффициента корреляции и коэффициента детерминации.

Для однофакторной модели: и по значениям коэффициента множественной корреляции и сов-го коэффициента детерминации.

Для моделей множественной регрессии: чем ближе абсолютные величины, указанных коэффициентов к 1, тем точнее связь между изучаемым признаком и выбранным фактором.

№ 11. Прогнозирование на базе регрессионных моделей.

При рассмотрении вопроса экономического прогнозирования на основе модели регрессии следует предположить, что модель, построенная на базе временных рядов изучаемого показателя и включенных в модель факторов, является адекватной и достаточно-точной.

При использовании построенной модели для прогнозирования делается также предположение о сохранении, существовавших ранее, взаимосвязи переменных.

Для прогнозирования зависимой переменной (результативного признака) на L-шагов вперед необходимо знать прогнозные значения всех входящих в модель факторов.

Эти значения могут быть получены на основе экстраполяционных методов. Они могут быть также определены методами экспертных оценок или непосредственно заданных исследователями.

прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.

Для определения области возможных значений результативного показателя при известных значениях факторов, т.е. доверительного интервала прогноза, необходимо учитывать 2 возможных источника ошибок: ошибки 1-го рода вызываются рассеиванием наблюдений относительно линии регрессии и их можно учесть в частности величиной средней квадратической ошибки апроксимации изучаемого показателя с помощью регрессионной модели; ошибки 2-го рода обусловлены тем, что в действительности жестко заданные модели коэффициенты регрессии являются случайными величинами распределенными по нормальному закону. Эти ошибки учитываются в вводах поправочного коэффициента при расчете ширины доверительного интервала.

Формула для расчета включает табличные значения t-ст-ки при заданном уровне значимости и зависит от вида регрессионной модели.

Для линейной однофакторной модели, общий вид которой y=а₀+а₁х_1, величина отклонения от линии регрессии задается выражением:

R(n,L,a)=t_aS_y * √1+1/n + (x_n+L – x)² / Σ (x_t– x)², где

n-число наблюдений;

L-количество шагов вперед;

a-уровень значимости прогноза;

x_t-наблюдаемость значения фактического признака в момент t;

x-среднее значение наблюдаемого признака;

x_n₊_L-прогнозное значение фактора на L-шагов вперед.

Таким образом, для рассматриваемой модели формула расчета нижней и верхней границ доверительного интервала прогноза имеет вид:

U_y=y*_n+L± R(n,L,a), где

y*_n₊_L-означает точечную прогнозную оценку изучаемого результативного показателя по модели на L-шагов вперед.

№ 12. Основные понятия и определения системы эконометрических уравнений.

При использовании отдельных уравнений регрессии,например, в экономических расчетах в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга, но это предположение весьма приближенно, т.к. практически изменение одной переменной не может происходить при абсолютной неизменности других.

Ее изменение повлечет за собой изменение по всей систем е взаимосвязанных признаков. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинное влияние отдельных признаков на вариацию результирующих переменных. Именно поэтому в экономических исследованиях важное место занимают системы одновременных уравнений, называемых также структурными уравнениями.

Например, при оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.

В еще большей степени возрастает потребность в использовании системы взаимосвязанных уравнений, если мы переходим от исследований на микроуровне к макроэкономическим расчетам.

Система уравнений может быть построена по-разному. Возможно система независимых уравнений, когда каждая независимая переменная y рассматривается как функция одного и того же набора фактора x:

y₁=a₁₁x₁+a₁₂x₂+…+a_1nx_n+E₁

y₂=a₂₁x₁+a₂₂x₂+…+a_2nx_n+E₂

…………………………….

y_m=a_m₁x₁+a_m₂x₂+…+a_mnx_n+E_m

Набор факторов x_i в каждом уравнении может варьировать. Так модель вида:

y₁=f(x₁,x₂,x₃,x₄,x₅)

y₂=f(x₁,x₃,x₄,x₅)

y₃=f(x₂,x₃,x₅)

y₄=f(x₃,x₄,x₅)

также является системой независимых уравнений с тем лишь отличием, что в ней набор факторов видоизменяется в уравнениях, входящих в систему.

Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения ее параметров используется МНК. Т.к. фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки. С учетом этого система независимых уравнений при 3-х зависимых переменных и 4-х факторов примет вид:

y₁=a₁₀+a₁₁x₁+a₁₂x₂+a₁₃x₃+a₁₄x₄+E₁

y₂=a₂₀+a₂₁x₁+a₂₂x₂+a₂₃x₃+a₂₄x₄+E₂

y₃=a₃₀+a₃₁x₁+a₃₂x₂+a₃₃x₃+a₃₄x₄+E₃

но если зависимая переменная y одного уравнения выступает в виде фактора х в другом уравнении, то исследователь может строить модель в виде системы рекурсивных моделей.

№ 13.Структурная форма эконометрической модели

Структурная форма эконометрической модели позволяет увидеть влияние изменения любой экзогенной переменной на значение эндогенной переменной. Целесообразно в качестве экзогенной переменной выбрать такие переменные, которые могут быть объектом регулирования, меняя их и управляя ими можно заранее иметь целевые значения эндогенных переменных. Простейшая структурная форма модели имеет вид:

y₁=b₁₂y₂+a₁₁x₁+ɛ₁;

y₂=b₂₁y₁+a₂₂x₂+ɛ₂.

где y-эндогенная переменная; x-экзогенная переменная.

В правой части при эндогенной и экзогенной переменных содержатся коэффициенты b_i и a_j, которые называют структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т.е. под x подразумевается x- , а под y соответственно y- . Поэтому свободный член в каждом уравнении данной системы отсутствует.

№ 14. Приведенная форма эконометрической модели.

Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:

y₁= ₁₁x₁+ ₁₂x₂+….+ _1nx_n

y₂= ₂₁x₁+ ₂₂x₂+….+ _2nx_n

…………………………

y_m= _m₁x₁+ _m₂x₂+….+ _mnx_n

где _i-коэффициент приведенной формы модели

Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели _ij через коэффициенты структурной модели: a_j и b_i. Для упрощения в модель не введены случайные переменные.

Для структурной модели вида:

y₁=b₁₂y₂+a₁₁x₁;

y₂=b₂₁y₂+a₂₂x₂

Приведенная форма модели имеет вид:

y₁= ₁₁x₁+ ₁₂x₂

y₂= ₂₁x₁+ ₂₂x₂

в которой y₂ из первого уравнения структурной модели можно выразить следующим образом: y₂= тогда система одновременных уравнений будет представлена как:

y₁=

y₂=b₂₁y₁+a₂₂x₂

Отсюда имеем равенство:

= b₂₁y₁+a₂₂x₂

a₁₁x₁=b₁₂b₂₁y₁+b₁₂a₂₂x₂

Тогда y₁-b₁₂b₂₁y₁=a₁₁x₁+b₁₂a₂₂x₂

y₁= .x₁+ .x₂

Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:

y₁= ₁₁x₁+ ₁₂x₂

Из уравнения следует, что коэффициенты приведенной формы модели представляют собой нелинейные соотношения коэффициентов структурной формы модели, то есть ₁₁= и ₁₂=

Аналогично можно показать, что коэффициенты приведенной формы модели второго уравнения системы ₂₁ и ₂₂также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную y₁ из второго структурного уравнения модели и после преобразований получим:

₂₁=