2015-03-08
2189
1.1.1. Если прямая l на плоскости проходит через точку N (x 0, y 0) перпендикулярно 
векто-ру 
=(A, B) (рис.1.1), то общее уравнение прямой l имеет вид
A (x - x 0)+ B (y - y 0)=0. (1.1) Как правило, общее уравнение (1.1) прямой приводят к виду
Ax + By + C =0, (1.2)
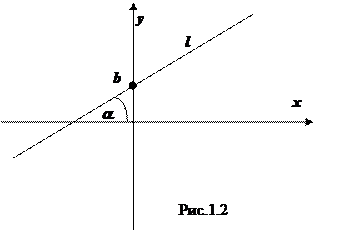где C =- Ax 0- By 0.
Вектор =(A, B) называется вектором нормали (или нормалью) прямой l.
1.1.2. Если прямая l не параллельна оси Oy, то явное уравнение прямой имеет вид
y = kx + b, (1.3)
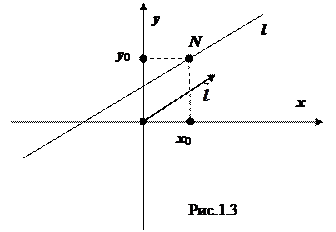где k =tg a, a - угол наклона прямой к оси Ox, b - ордината точки пересечения прямой с осью Oy. k называется угловым коэффициентом прямой l, уравнение (1.3) - уравнением прямой с угловым коэффициентом.
1.1.3. Если прямая l проходит через точку N (x 0, y 0) параллельно вектору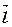 
=(a, b) (рис.1.3), то параметрические уравнения прямой l имеют вид
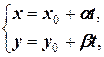(1.4)
Вектор 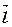=(a, b) называется направляющимвектором прямой l.
1.1.4. Кроме общего, явного и параметрического уравнений прямой также рассматриваются другие виды уравнений:
каноническое: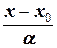 
= 
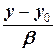, (1.5)
где (a, b) - направляющий вектор прямой, (x 0, y 0) - некоторая точка прямой;
уравнение прямой, проходящей через точкиN (x 0, y 0), M (x 1, y 1):
= 
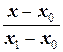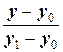, (1.6)
уравнение прямой в отрезках: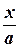 
+ 
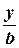=1, (1.7)
при условии, что прямая не параллельна ни одной из осей координат.
1.1.5. Замечания. 1) С помощью тождественных преобразований из одного вида уравнений можно прийти к другому. Например, если B ≠0, то из общего уравнения можно прийти к уравнению с угловым коэффициентом: y=-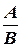 
x -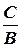 
. Обратно, из уравнения (1.3) получается общее: - kx + y - b =0. Далее, исключая параметр t из (1.4), можно прийти к (1.5), И т.д.
2) В частных случаях, когда прямая параллельна одной из осей, общее уравнение (1.2) записывается в виде x = a (если прямая параллельна оси Oy) или y = b (если прямая параллельна оси Ox) (рис. 1.4).
3) В каноническом уравнении (1.5) допускается, чтобы a =0 или b =0 (но не одновременно!). В этом уравнении дроби не обозначают операцию деления. Например, уравнение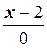 
= 
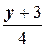означает, что прямая проходит через точку (2; -3) параллельно вектору (0; 4).
4) По сути уравнение (1.6) является каноническим уравнением прямой с направляющим вектором (x 1- x 0; y 1- y 0).
5) Геометрический смысл параметров a и b в уравнении (1.7) следующий: a и b - соответственно абсцисса и ордината точек пересечения прямой с осями соответственно Ox и Oy (рис. 1.5).
1.1.6. Упражнения. 1) Написать различные уравнения прямой и изобразить прямые в системе координат:
а) проходящей через точку N (3; -2) перпендикулярно вектору 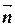=(4; -2);
б) проходящей через точку N (2; 4) перпендикулярно вектору 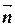=(3; 8);
в) проходящей через точку N (4; 2) параллельно вектору 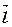=(3; -1);
г) проходящей через точку N (5; -8) параллельно вектору 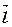=(2; 3);
д) проходящей через точку N (2; -1) и M (3; -4);
е) проходящей через точку N (3; 2) и M (4; -5).
Решение. а) По формуле (1.1) имеем 4(x -3)-2(y +2)=0. Преобразуем его к виду (1.2): 4 x -2 y -16=0. Это - общее уравнение прямой. Его можно сократить на 2: 2 x - y -8=0.
Приведём к уравнению с угловым коэффициентом: y =2 x -8.
Напишем параметрические и каноническое уравнения. Для этого заметим, что вектор 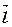=(1; 2) будет направляющим, так как
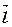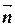(, )=1×4+2×(-2)=0,
то есть 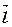^ 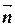и поэтому 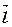параллелен l. Отсюда по (1.4)
= 
-
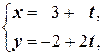
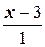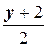- параметрические и каноническое уравнения соответственно.
Для получения уравнения в отрезках применим к общему уравнению тождественные преобразования:
2 x - y -8=0 Û 2 x - y =8 Û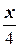 
- 
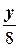=1 Û + 
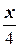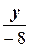=1,
то есть 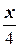+ 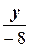=1 - уравнение прямой в отрезках.
в) Напишем сначала каноническое уравнение прямой: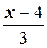 
= 
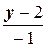. Для написания общего уравнения применим тождественные преобразования к этому равнению:
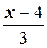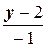= Û (-1)(x -4)=3(y -4) Û - x +4=3 y -6 Û
Û - x -3 y +10=0 Û - x -3 y +10=0 Û x +3 y -10=0,
то есть x +3 y -10=0 - общее уравнение прямой (как правило, коэффициент при х приводят к знаку «+». Остальное - как в а) (довести до конца!).
д) Напишем уравнение прямой, проходящей через две точки:
= 
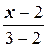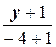Û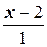 
= 
.
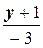Остальное - как и выше (довести до конца).
Ответ: а) 2 x - y -8=0 - общее уравнение прямой,
y =2 x -8 - уравнение прямой с угловым коэффициентом,
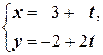- параметрические уравнения прямой,
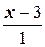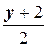= - каноническое уравнение прямой,
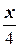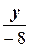+ =1 - уравнение прямой в отрезках.
2) Известны угол a наклона прямой к оси Ox и точка N, через которую проходит прямая. Написать уравнение прямой:
а) a =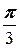 
, N (4; 2);
б) a =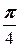 
, N (2; -1);
в) a =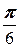 
, N (3; -8).
Решение. а) Напишем уравнение с угловым коэффициентом: y = kx + b, где k =tg =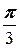 
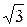, то есть y = 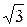x + b. Так как N (4; 2) принадлежит прямой, то её координаты удовлетворяют уравнению прямой: 2= 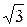×4+ b, откуда b =2-4 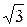. Окончательно имеем y = 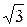x +2-4 .
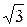Ответ: а) y = 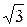x +2-4 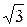- уравнение прямой с угловым коэффициентом.
