Физическое и математическое моделирование

Контрольные вопросы

Классификация систем

Признаки систем

Основные признаки систем следующие:

· целостность, связанность или относительная независимость от среды и систем. С исчезновением связанности исчезает и система, хотя элементы системы и даже некоторые отношения между ними могут быть сохранены;

· наличие подсистем и связей между ними или наличие структуры системы. С исчезновением подсистем или связей между ними может исчезнуть и сама система;

· возможность обособления или абстрагирования от окружающей среды, т.е. относительная обособленность от тех факторов среды, которые в достаточной мере не влияют на достижение цели;

· связи с окружающей средой по обмену ресурсами;

· подчиненность всей организации системы некоторой цели;

· эмерджентность или несводимость свойств системы к свойствам элементов;

· увеличение разнообразия типов частей системы, выполняемых ими функций, что обусловливает различия в их абсолютной стоимости;

· усложнение функционирования;

· сложность поведения, нелинейность характеристик;

· повышение уровня автоматизации, означающее, в частности, увеличение степени относительной самостоятельности системы в ее поведении;

· нерегулярное, статистически распределенное во времени поступление внешний воздействий;

· наличие в ряде случаев состязательного момента, т.е. такого функционирования системы, при котором необходимо учитывать конкуренцию отдельных частей;

· многоаспектность (техническая, экономическая, социальная, психологическая);

· контринтуитивность (причина и следствие жестко однозначно не связаны ни во времени, ни в пространстве);

· нелинейность (синергетика).

Системы разделяются на классы по различным признакам, и в зависимости от решаемой задачи можно выбрать разные принци­пы классификации. При этом систему можно охарактеризовать одним или несколькими признаками. Чаще всего системы классифицируются следующим образом:

· по виду научного направления - математические, физи­ческие, химические и т. п.;

· по степени определенности функционирования: детерминированные и вероятностные. Детерминированной называют систему, если ее поведение можно абсолютно точно предвидеть. Система, состояния которой зависит не только от контролируемых, но и от неконтролируемых воздействий или если в ней самой находится источник случайности, носит название вероятностной. Приведем пример стохастических систем, это - заводы, аэропорты, сети и системы ЭВМ, магазины, предприятия бытового обслуживания и т.д.

· по степени организованности - хорошо организован­ные, плохо организованные (диффузные), самоорганизующиеся системы.

· по происхождению различают системы естественные, созданные в ходе естественной эволюции и в целом не подверженные влиянию человека (клетка), и искусственные, созданные под воздействием человека, обусловленные его интересами и целями (машина).

· по основным элементам системы могут быть разделены на абстрактные, все элементы которых являются понятиями (языки, философские системы, системы счисления), и конкретные, в которых присутствуют материальные элементы.

· по взаимодействию со средой различают системы замкнутые и открытые. Замкнутая система в процессе своего функционирования использует только ту информацию, которая вырабатывается в ней самой (система кондиционирования воздуха в замкнутом объеме). В открытойсистеме функционирование определяется как внутренней, так и внешней, поступающей на входы, информацией. Большинство изучаемых систем являются открытыми, т.е. они испытывают воздействие среды и реагируют на него и, в свою очередь, оказывают воздействие на среду.

· по степени сложности различают простые, сложные и очень сложные системы. Простые системы характеризуются небольшим числом элементов, связи между которыми легко поддаются описанию (средства механизации, простейшие организмы). Сложные системы состоят из большого числа элементов и характеризуются разветвленной структурой, выполняют более сложные функции. Изменения отдельных элементов и (или) связей влечет за собой изменение многих других элементов. Но все же отдельные конкретные состояния системы могут быть описаны (автоматы, ЭВМ, галактики). Очень сложные системы характеризуются большим числом разнообразных элементов, обладают множеством структур, не могут быть полностью описаны (мозг, хозяйство).

· по естественному разделению системы делятся на: технические, биологические, социально-экономические. Технические – это искусственные системы, созданные человеком (машины, автоматы, системы связи). Биологические – различные живые организмы, популяции, биогеоценозы и т.п. Социально-экономические – системы существующие в обществе, обусловленные присутствием и деятельностью человека (хозяйство, отрасль, бригада и т.п.).

· по определению выходных сигналов. Динамические системы характеризуются тем, что их выходные сигналы в данный момент времени определяются характером входных воздействий в прошлом и настоящем (зависит от предыстории). В противном случае системы называют статическими. Примером динамических систем является биологические, экономические, социальные системы; такие искусственные системы как завод, предприятия, поточная линия и т.д.

· по изменению во времени. Если вход и выход системы измеряется или изменяется во времени дискретно, через шаг t, то система называется дискретной. Противоположным понятием является понятие непрерывной системы. Например: ЭВМ, электронные часы, электросчетчик - дискретные системы; песочные часы, солнечные часы, нагревательные приборы и т.д. - непрерывные системы.

· По типу организации: централизованные (однополюсные, иерархические, биполярные с входным и выходным полюсами); децентрализованные (многополюсные сети, сети без полюсов с различной произвольной топологией; матрич­ные сети с регулярной топологией, сети смешанной топо­логии: регулярной и произвольной)

· По составу функций: одно- или многофункциональ­ные, с постоянным или переменным составом функций;

Объектом изучения системного анализа являются в большинстве своем стохастические открытые сложные и очень сложные системы любого происхождения.

Рассмотрим некоторые виды систем более подробно.

Хорошо организованные системы. Представить анализируемый объект или процесс в виде «хорошо организованной системы» означает определить элементы системы, их взаимосвязь, правила объединения в более крупные компоненты, т. е. определить связи между всеми компонентами и целями системы, с точки зрения которых рассматривается объект или ради достижения которых создается система. Проблемная ситуация может быть описана в виде математического выражения, связывающего цель со сред­ствами, т. е. в виде критерия эффективности, критерия функци­онирования системы, который может быть представлен сложным уравнением или системой уравнений. Решение задачи при пред­ставлении ее в виде хорошо организованной системы осуществ­ляется аналитическими методами формализованного представле­ния системы.

Примеры хорошо организованных систем: солнечная система, описывающая наиболее существенные закономерности движения планет вокруг Солнца; отображение атома в виде планетарной системы, состоящей из ядра и электронов; описание работы сложного электронного устройства с помощью системы уравне­ний, учитывающей особенности условий его работы (наличие шумов, нестабильности источников питания и т. п.). Для отображения объекта в виде хорошо организованной системы необходимо выделять существенные и не учитывать относительно несущественные для данной цели рассмотрения компоненты: например, при рассмотрении солнечной системы не учитывать метеориты, астероиды и другие мелкие по сравнению с планетами элементы межпланетного пространства.

Описание объекта в виде хорошо организованной системы применяется в тех случаях, когда можно предложить детермини­рованное описание и экспериментально доказать правомерность его применения, адекватность модели реальному процессу. По­пытки применить класс хорошо организованных систем для представления сложных многокомпонентных объектов или мно­гокритериальных задач плохо удаются: они требуют недопусти­мо больших затрат времени, практически нереализуемы и неадек­ватны применяемым моделям.

Плохо организованные системы. При представлении объекта в виде «плохо организованной или диффузной системы» не ста­вится задача определить все учитываемые компоненты, их свой­ства и связи между ними и целями системы. Система харак­теризуется некоторым набором макропараметров и закономер­ностями, которые находятся на основе исследования не всего объекта или класса явлений, а на основе определенной с помо­щью некоторых правил выборки компонентов, характеризующих исследуемый объект или процесс. На основе такого выборочного исследования получают характеристики или закономерности (статистические, экономические) и распространяют их на всю систему в целом. При этом делаются соответствующие оговорки. Например, при получении статистических закономерностей их распространяют на поведение всей системы с некоторой довери­тельной вероятностью.

Подход к отображению объектов в виде диффузных систем широко применяется при: описании систем массового обслужива­ния, определении численности штатов на предприятиях и учреж­дениях, исследовании документальных потоков информации в си­стемах управления и т. д.

Самоорганизующиеся системы. Отображение объекта в виде самоорганизующейся системы — это подход, позволяющий ис­следовать наименее изученные объекты и процессы. Самооргани­зующиеся системы обладают признаками диффузных систем: стохастичностью поведения, нестационарностью отдельных па­раметров и процессов. К этому добавляются такие признаки, как непредсказуемость поведения; способность адаптироваться к из­меняющимся условиям среды, изменять структуру при взаимо­действии системы со средой, сохраняя при этом свойства целост­ности; способность формировать возможные варианты поведе­ния и выбирать из них наилучший и др. Иногда этот класс разбивают на подклассы, выделяя адаптивные или самоприс­посабливающиеся системы, самовосстанавливающиеся, самовос­производящиеся и другие подклассы, соответствующие различ­ным свойствам развивающихся систем. Примеры: биологические организации, коллективное поведение людей, организация управления на уровне предприятия, отрасли, государства в целом, т.е. в тех системах, где обязательно имеется человеческий фактор.

При применении отображения объекта в виде самоорганизующейся системы задачи определения целей и выбора средств, к; правило, разделяются. При этом задача выбора целей может быть, в свою очередь, описана в виде самоорганизующейся системы, т. е. структура функциональной части АСУ, структура целей плана может разбиваться так же, как и структура обеспечивающей части АСУ (комплекс технических средств АСУ) или организационная структура системы управления.

Большинство примеров применения системного анализа основано на представлении объектов в виде самоорганизующихся систем.

Большие и сложные системы. Существует ряд подходов к разделению систем по сложности. В частности, Г. Н. По варовв зависимости от числа элементов, входящих в систему, выделяет четыре класса систем: малые системы (10...10³ элементов), сложные (10⁴...10⁷ элементов), ультрасложные (10⁷...10³⁰ элементов) суперсистемы (10³⁰...10²⁰⁰ элементов). Так как понятие элемент; возникает относительно задачи и цели исследования системы, то и данное определение сложности является относительным, а не абсолютным.

Английский кибернетик С. Бир классифицирует все кибернетические системы на простые и сложные в зависимости от способа описания: детерминированного или теоретико-вероятностного. А. И. Берг определяет сложную систему как систему, которую можно описать не менее чем на двух различных мате­матических языках (например, с помощью теории дифференци­альных уравнений и алгебры Буля).

Очень часто сложными системами называют системы, кото­рые нельзя корректно описать математически, либо потому, что в системе имеется очень большое число элементов, неизвестным образом связанных друг с другом, либо неизвестна природа явлений, протекающих в системе. Все это свидетельствует об отсутствии единого определения сложности системы.

Так же дается следующее определение: сложной системой называется система, в модели которой недостаточно информации для эффективного управления этой системой. Таким образом, признаком простоты системы является достаточность информации для ее управления. Если же результат управления, полученный с помощью модели, будет неожиданным, то такую систему относят к сложной. Для перевода системы в разряд простой необходимо получение недостающей информации о ней и включение ее в модель.

При разработке сложных систем возникают проблемы, относящиеся не только к свойствам их составляющих элементов и подсистем, но также к закономерностям функционирования системы в целом. При этом появляется широкий круг специфи­ческих задач, таких, как определение общей структуры системы; организация взаимодействия между элементами и подсистемами; учет влияния внешней среды; выбор оптимальных режимов функ­ционирования системы; оптимальное управление системой и др.

Чем сложнее система, тем большее внимание уделяется вышеуказанным вопросам. Математической базой исследования сложных систем является теория систем. В теории систем большой системой сложной, системой большого масштаба,(Large Scale Systems) называют систему, если она состоит из большого числа взаимосвязанных и взаимодействующих между собой элементов и способна выполнять сложную функцию.

От сложных систем необходимо отличать большие системы.

Под большой системой понимается совокупность материаль­ных ресурсов, средств сбора, передачи и обработки информации, людей-операторов, занятых на обслуживании этих средств, и лю­дей-руководителей, облеченных надлежащими правами и ответ­ственностью для принятия решений. Материальные ресурсы - это сырье, материалы, полуфабрикаты, денежные средства, раз­личные виды энергии, станки, оборудование, люди, занятые на выпуске продукции, и т. д. Все указанные элементы ресурсов объединены с помощью некоторой системы связей, которые по заданным правилам определяют процесс взаимодействия между элементами для достижения общей цели или группы целей. Таким образом, с истема, для актуализации модели которой в целях управления недостает материальных ресурсов (машинного времени, емкости памяти, других материальных средств моделирования) называется большой. К таким системам относятся экономические, организационно-управленческие, биологические нейрофизиологические, и т.п. системы.

Характерные особенности больших систем. К подобным отличительным особенностям относятся следующие:

· большое число элементов в системе (сложность системы);

· взаимосвязь и взаимодействие между элементами;

· иерархичность структуры управления;

· обязательное наличие человека в контуре управления, на которого возлагается часть наиболее ответственных функций управления.

Примеры больших систем: информационная система; пассажирский транспорт крупного города; производственный процесс; система управления полетом крупного аэродрома; энергетическая система и др.

Способом перевода больших систем в простые является создание новых более мощных средств вычислительной техники. Однако, четкой границы, отделяющей простые системы от больших, нет. Деление это условное и возникло из-за появления систем, имеющих в своем составе совокупность подсистем с наличием функциональной избыточности. Простая система может находиться только в двух состояниях: состоянии работоспособности (исправном) и состоянии отказа (неисправном). При отказе элемента простая система либо полностью прекращает выполнение своей функции, либо продолжает ее выполнение в полном объеме, если отказавший элемент резервирован. Большая система при отказе отдельных элементов и даже целых подсистем не всегда теряет работоспособность, зачастую только снижаются характеристики ее эффективности. Это свойство больших систем обусловлено их функциональной избыточностью и, в свою очередь, затрудняет формулировку понятия «отказ» системы.

1. Что представляет собой общая теория систем?

2. Что такое кибернетика?

3. Что такое теория информации?

4. Что такое теория игр?

5. Что такое факторный анализ?

6. Опишите подходы к созданию общей теории систем?

7. Раскройте понятие «система».

8. В чем особенности сложной системы?

9. Чем сложные системы отличаются от больших систем?

10. Дайте определения следующим понятиям: объект, подсистема, структура, функция, связь.

11. Опишите основные закономерности систем.

12. Дайте классификацию систем по основным признакам.

13. Опишите отличие сложных систем от больших.

Тема№4
Моделирование систем

4.1. Понятия «модель» и «моделирование». Абстрактная модель системы произвольной природы

Так как общая теория систем рассматривает не некоторые конкретные системы, а то общее, что есть в различных системах независимо от их природы, предметом ее изучения являются абстрактные модели соответствующих реальных систем.

Модель является представлением реального объекта, системы или понятия в некоторой форме, отличной от формы их реального существования.

Всякая модель - это некоторая аналогия: для одной системы должна существовать другая система, элементы которой с некоторой точки зрения подобны элементам первой. Должно существовать отображение, которое элементам моделируемой системы ставит в соответствие элементы некоторой другой системы - моделирующей. Кроме того, должно существовать отображение, которое свойствам элементов моделируемой системы ставит в соответствие свойства элементов моделирующей системы.

Рис 4.1. Абстрактная модель системы произвольной природы

Для большинства случаев абстрактная модель системы произвольной природы может быть представлена с помощью схемы, изображенной на рисунке 4.1, которая является, по сути, иллюстрацией к введенным понятиям.

Система не существует сама по себе, а выделяется из окружающей среды по какому-либо системообразующему признаку, в качестве которого чаще всего выступает цель системы. Взаимодействие системы с внешней средой осуществляется через вход и выход системы (множество входных и выходных параметров).

Под входными параметрами системы понимается комплекс параметров внешней среды (в том числе выходные параметры систем, внешних по отношению к рассматриваемой, например, систем управления), оказывающих значительное влияние на состояние и значение выходных параметров рассматриваемой системы и поддающихся учету и анализу средствами, имеющимися в распоряжении исследователя.

Выходные параметры - это комплекс параметров системы, оказывающих непосредственное влияние на состояние внешней среды и значимых с точки зрения цели исследования.

Важной особенностью функционирования сложных систем является принципиальная неопределенность истинного состояния внешней среды в каждый момент времени. Природа этой неопределенности связана с наличием ряда причин, важнейшие из которых обусловлены следующими факторами.

· О некоторых, возможно, непосредственно влияющих на поведение системы параметрах внешней среды (то есть параметрах, которые следовало бы отнести к категории «входных») исследователь часто не знает, и, следовательно, не может их учитывать.

· Некоторые параметры внешней среды не могут быть измерены в силу технической неприспособленности информационных средств.

· Численные значения учитываемых параметров оцениваются с ошибками измерений, определяемыми с одной стороны - внутренними шумами измерительных устройств, а с другой - внешними помехами.

Воздействие на систему подобных неучтенных факторов компенсируется введением в модель дополнительных связей - внешних возмущающих воздействий или «шумов».

Система может находиться в различных состояниях. Состояние любой системы в определенный момент времени можно с определенной точностью охарактеризовать совокупностью значений параметров состояния .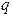

Таким образом, система характеризуется тремя группами переменных:

1. Входные переменные, которые генерируются системами, внешними относительно исследуемой

;

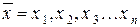2. Выходные переменные, определяющие воздействие исследуемой системы на окружающую среду

;

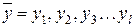3. Параметры состояния, характеризующие динамическое поведение исследуемой системы

.

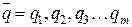При исследовании большинства систем все три группы введенных величин предполагаются функциями времени.

Так как понятие «моделирование» является достаточно общим и универсальным, к числу способов моделирования относятся столь различные подходы как, например, метод мембранной аналогии (физическое моделирование) и методы линейного программирования (оптимизационное математическое моделирование). Для того чтобы упорядочить употребление термина «моделирование» вводят классификацию различных способов моделирования. В наиболее общей форме выделяются две группы различных подходов к моделированию, определяемых понятиями «физическое моделирование» и «идеальное моделирование».

Физическое моделирование осуществляется путем воспроизведения исследуемого процесса на модели, имеющей в общем случае отличную от оригинала природу, но одинаковое математическое описание процесса функционирования.

Совокупность подходов к исследованию сложных систем, определяемая термином «математическое моделирование», является одной из разновидностей идеального моделирования. Математическое моделирование основано на использовании для исследования системы совокупности математических соотношений (формул, уравнений, операторов и т.д.), определяющих структуру исследуемой системы и ее поведение.

Математическая модель - это совокупность математических объектов (чисел, символов, множеств и т.д.), отражающих важнейшие для исследователя свойства технического объекта, процесса или системы.

Математическое моделирование - это процесс создания математической модели и оперирования ею с целью получения новой информации об объекте исследования.

Построение математической модели реальной системы, процесса или явления предполагает решение двух классов задач, связанных с построением «внешнего» и «внутреннего» описания системы. Этап, связанный с построением внешнего описания системы называется макроподходом. Этап, связанный с построением внутреннего описания системы называется микроподходом.

Макроподход - способ, посредством которого производится внешнее описание системы. На этапе построения внешнего описания делается упор на совместное поведение всех элементов системы, точно указывается, как система откликается на каждое из возможных внешних (входных) воздействий 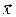. Система рассматривается как «черный ящик», внутреннее строение которого неизвестно. В процессе построения внешнего описания исследователь имеет возможность, воздействуя различным образом на вход системы, анализировать ее реакцию на соответствующие входные воздействия. При этом степень разнообразия входных воздействий принципиальным образом связана с разнообразием состояний выходов системы. Если на каждую новую комбинацию входных воздействий система реагирует непредсказуемым образом, испытание необходимо продолжать. Если на основании полученной информации может быть построена система, в точности повторяющая поведение исследуемой, задачу макроподхода можно считать решенной.

Итак, метод «черного ящика» состоит в том, чтобы выявить, насколько это возможно, структуру системы и принципы ее функционирования, наблюдая только входы и выходы. Подобный способ описания системы некоторым образом аналогичен табличному заданию функции.

При микроподходе структура системы предполагается известной, то есть предполагается известным внутренний механизм преобразования входных сигналов в выходные. Исследование сводится к рассмотрению отдельных элементов системы. Выбор этих элементов неоднозначен и определяется задачами исследования и характером исследуемой системы. При использовании микроподхода изучается структура каждого из выделенных элементов, их функции, совокупность и диапазон возможных изменений параметров.

Микроподход - способ, посредством которого производится внутреннее описание системы, то есть описание системы в функциональной форме.

Результатом этого этапа исследования должен явиться вывод зависимостей, определяющих связь между множествами входных параметров, параметров состояния и выходных параметров системы. Переход от внешнего описания системы к ее внутреннему описанию называют задачей реализации.

Задача реализации заключается в переходе от внешнего описания системы к ее внутреннему описанию. Задача реализации представляет собой одну из важнейших задач в исследовании систем и, по существу, отражает абстрактную формулировку научного подхода к построению математической модели. В такой постановке задача моделирования заключается в построении множества состояний и вход-выходного отображения исследуемой системы на основе экспериментальных данных. В настоящее время задача реализации решена в общем виде для систем, у которых отображение вход-выход линейно. Для нелинейных систем общего решения задачи реализации пока не найдено.