Непрерывная случайная величина Х задана своей плотностью распределения вероятностей 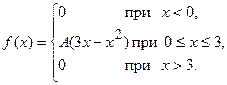
Требуется:
a. найти коэффициент А;
b. найти функцию распределения F (x);
c. построить график функций f (x) и F (x);
d. найти математическое ожидание и дисперсию Х;
e. найти вероятность того, что Х примет значение из интервала (α, β), если
α = 1, β = 2.
Решение:
1) Так как все значения случайной величины заключены в промежутке [0,3], то 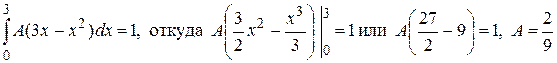 .
.
2) Воспользуемся формулой 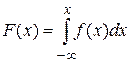 .
.
Если x <0, то f (x) = 0 и 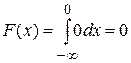 .
.
Если 0 ≤ х ≤ 3, то 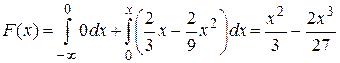 .
.
Если х > то 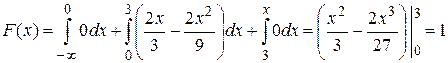 .
.
Искомая функция распределения имеет вид:
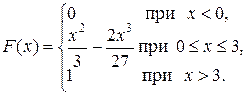
3) Строим графики функций f (x) и F (x):
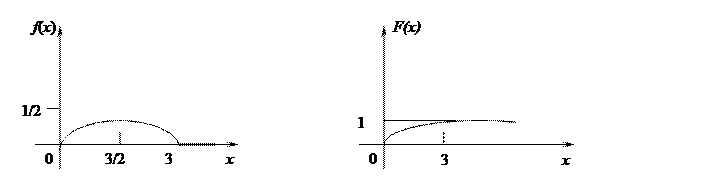
Рис. 1 Рис. 2
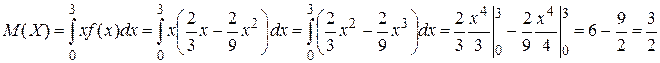 .
.
Дисперсия:
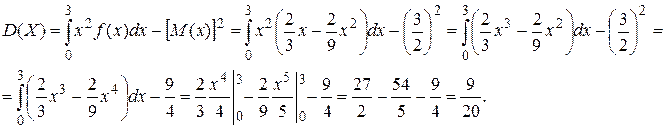
5) 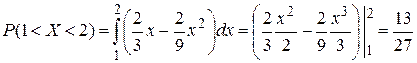 .
.
Пример 11. Дана функция распределения непрерывной случайной величины Х
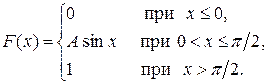
Найти параметр А и плотность распределения f (x).
Решение. 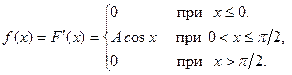
Известно, что 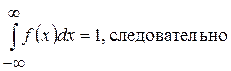 ,
, 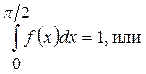
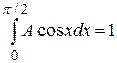 , откуда
, откуда 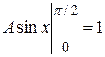 , или А = 1. Таким образом
, или А = 1. Таким образом
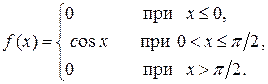
Пример 12. Нормально распределенная случайная величина Х задана своими параметрами а = 30 и σ = 10. Требуется:
1) написать плотность вероятности и схематически построить ее график;
2) определить вероятность попадания Х в интервале (10, 50);
3) определить вероятность того, что Х отклонится (по модулю) от а = 30 не более чем на 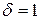 .
.
15. Решение. По заданным параметрам случайной величины Х плотность вероятности будет иметь вид 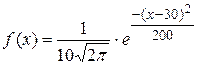
Схематически строим график: 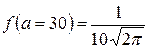 ;
; 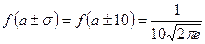
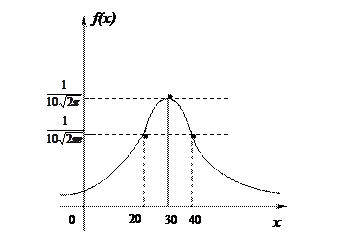
Рис. 3
2) Применяя формулу 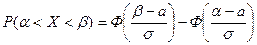 , получим
, получим
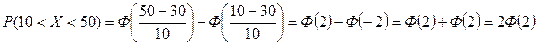 .
.
По таблице значений функции Лапласа находим 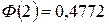 . Следовательно Р (10< X <50) = 2∙0,4772=0,9544.
. Следовательно Р (10< X <50) = 2∙0,4772=0,9544.
3) Вероятность отклонения находим по формуле
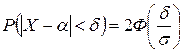 . Подставив данные, получим
. Подставив данные, получим
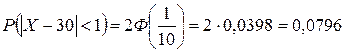 , где по таблице
, где по таблице 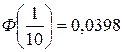 .
.
Пример 13. Дана выборка:
Требуется:
1) определить размах варьирования значений СВ Х и составить вариационный ряд распределения СВ Х;
2) составить интервальный вариационный ряд распределения;
3) найти выборочное среднее 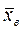 , выборочную дисперсию Dв, выборочное среднее квадратическое отклонение σ в, моду М о, медиану Ме и коэффициент вариации δ в выборки;
, выборочную дисперсию Dв, выборочное среднее квадратическое отклонение σ в, моду М о, медиану Ме и коэффициент вариации δ в выборки;
4). построить эмпирическую функцию распределения F*(х).
5) построить гистограмму относительных частот и линию эмпирической плотности;
6) пользуясь критерием Пирсона проверить гипотезу о нормальном законе распределения генеральной совокупности при уровне значимости α = 0,05, предварительно вычислив для каждого интервала группирования вариационного ряда выравнивающие частоты;
7) на гистограмме относительных частот нанести линию плотности f (x) нормального распределения;
8) найти доверительный интервал для неизвестного математического ожидания М (Х) генеральной совокупности случайной величины с надежностью γ = 0,95.
Решение: 1. Объем выборки п = 100, минимальное значение xmin = 46, максимальное хmax = 85, размах варьирования R = 39.
Составляем вариационный ряд:
Таблица 1
| xi | |||||||||||||||||
| ni |
| xi | |||||||||||||||||||
| ni |
Проверка: 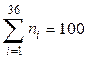 (объем выборки).
(объем выборки).
2. По формуле Стерджеса определяем длину интервалов h
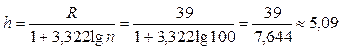 .
.
Округляем полученное значение до ближайшего целого числа. Принимаем длину интервала h = 5. За начало интервала принимаем значение 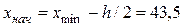 . Составляем интервальный вариационный ряд распределения СВ Х, группируя исходные данные в интервалы с шагом h. Число интервалов k = 9.
. Составляем интервальный вариационный ряд распределения СВ Х, группируя исходные данные в интервалы с шагом h. Число интервалов k = 9.
Таблица 2
| № интервала | Границы интервалов | Частоты пi | Относительные частоты wi | Середины интервалов 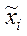 | Плотность частоты wi / h | Накопленные частости wi нак. | ||
| начало xi | конец xi +1 | |||||||
| 43,5 | 48,5 | 0,02 | 0,004 | 0,02 | ||||
| 48,5 | 53,5 | 0,11 | 0,022 | 0,13 | ||||
| 53,5 | 58,5 | 0,12 | 0,024 | 0,25 | ||||
| 58,5 | 63,5 | 0,15 | 0,030 | 0,40 | ||||
| 63,5 | 68,5 | 0,21 | 0,042 | 0,61 | ||||
| 68,5 | 73,5 | 0,15 | 0,030 | 0,76 | ||||
| 73,5 | 78,5 | 0,15 | 0,030 | 0,91 | ||||
| 78,5 | 83,5 | 0,05 | 0,010 | 0,96 | ||||
| 83,5 | 88,5 | 0,04 | 0,008 | 1,00 | ||||
| Контроль | 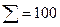 | 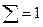 | ||||||
3. Находим выборочное среднее 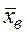 , выборочную дисперсию Dв, выборочное среднее квадратическое отклонение
, выборочную дисперсию Dв, выборочное среднее квадратическое отклонение 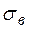 , моду Мо, медиану Ме и коэффициент вариации δв.
, моду Мо, медиану Ме и коэффициент вариации δв.
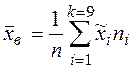 ;
; 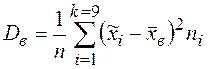 ;
; 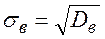 .
.
Для контроля вычислений и исключения арифметических ошибок целесообразно расчеты сумм, входящих в формулы 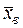 и Dв провести с помощью табл. 3 следующего вида:
и Dв провести с помощью табл. 3 следующего вида:
Таблица 3
| пi | 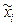 | 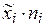 | 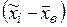 | 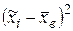 | 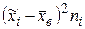 |
| -19,8 | 392,04 | 784,08 | |||
| -14,8 | 219,04 | 2409,94 | |||
| -9,8 | 96,04 | 1152,48 | |||
| -4,8 | 23,04 | 345,60 | |||
| 0,2 | 0,04 | 0,84 | |||
| 5,2 | 27,04 | 405,60 | |||
| 10,2 | 104,04 | 1560,60 | |||
| 15,2 | 231,04 | 1155,20 | |||
| 20,2 | 408,04 | 1632,16 | |||
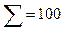 | - | 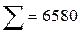 | - | - | 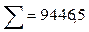 |
Окончательно получим: 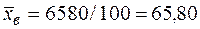 ;
;
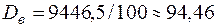 ;
;
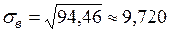 .
.
По вариационному ряду (табл.1) устанавливаем величины моды и медианы выборки: 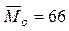 (или 67) – значения выборки имеют наибольшую частоту;
(или 67) – значения выборки имеют наибольшую частоту; 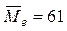 – значения серединного элемента вариационного ряда.
– значения серединного элемента вариационного ряда.
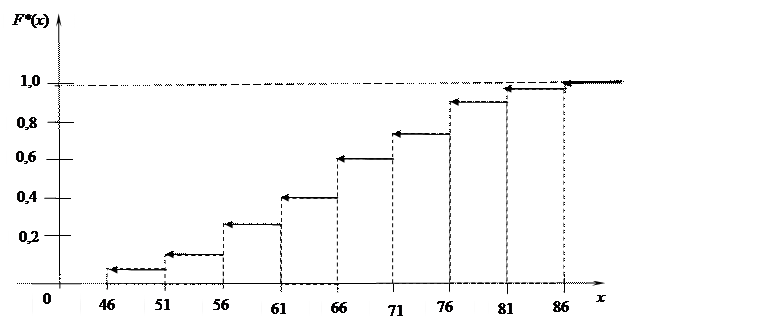
4. Построим эмпирическую функцию распределения F* (x). Используя данные таблицы 2 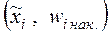 находим значения этой функции, а затем строим график.
находим значения этой функции, а затем строим график.
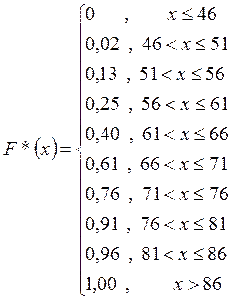
(указаны середина интервалов 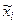 )
)
Рис. 4
5. Строим гистограмму относительных частот, используя данные таблицы 2.
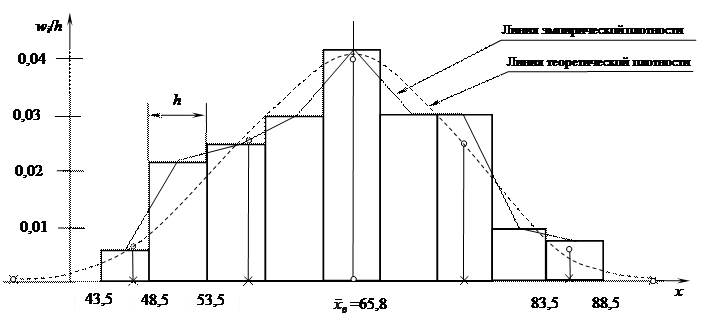
(указаны границы интервалов)
Рис. 5
Соединив отрезками прямых середины верхних сторон прямоугольников, получаем линию эмпирической плотности.
По виду гистограммы относительных частот и линии эмпирической плотности принимаем нулевую гипотезу Но о том, что распределение рассматриваемой СВ Х подчиняется нормальному закону распределения.
6. Для каждого интервала варьирования, используя данные таблицы 2 предыдущего примера, находим теоретические выравнивающие частоты по формуле
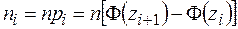 ,
,
где Φ (z) – табличные значения функции Лапласа, 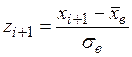 ,
, 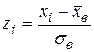 .
.
В рассматриваем примере 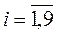 (девять интервалов),
(девять интервалов), 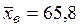 , σв = 9,72, п = 100. Данные расчеты представим в таблице 4. При использовании приведенной формулы теоретических частот наименьшее значение аргумента функции Лапласа zi для первого интервала выборки принято равным –∞ (Φ (- ∞) = –0,5), а наибольшее значение аргумента zi +1 для последнего интервала +∞ (Φ (+∞) = 0,5).
, σв = 9,72, п = 100. Данные расчеты представим в таблице 4. При использовании приведенной формулы теоретических частот наименьшее значение аргумента функции Лапласа zi для первого интервала выборки принято равным –∞ (Φ (- ∞) = –0,5), а наибольшее значение аргумента zi +1 для последнего интервала +∞ (Φ (+∞) = 0,5).
Таблица 4
| № интервала | Границы интервалов | zi | zi+ 1 | Φ (zi) | Φ (zi+1) | Φ (zi+1) – Φ (zi) | пТi | |
| xi | xi+ 1 | |||||||
| 43,5 | 48,5 | -∞ | -1,78 | -0,5 | -0,4625 | 0,0375 | 3,75 | |
| 48,5 | 53,5 | -1,78 | -1,26 | -0,4625 | -0,3962 | 0,0663 | 6,63 | |
| 53,5 | 58,5 | -1,26 | -0,75 | -0,3962 | -0,2734 | 0,1228 | 12,28 | |
| 58,5 | 63,5 | -0,75 | -0,24 | -0,2734 | -0,0948 | 0,1786 | 17,86 | |
| 63,5 | 68,5 | -0,24 | 0,28 | -0,0948 | 0,1103 | 0,2051 | 20,51 | |
| 68,5 | 73,5 | 0,28 | 0,79 | 0,1103 | 0,2852 | 0,1749 | 17,49 | |
| 73,5 | 78,5 | 0,79 | 1,31 | 0,2852 | 0,4049 | 0,1197 | 11,97 | |
| 78,5 | 83,5 | 1,31 | 1,82 | 0,4049 | 0,4656 | 0,0607 | 6,07 | |
| 83,5 | 88,5 | 1,82 | +∞ | 0,4656 | 0,5 | 0,0344 | 3,44 | |
| Σрi = 1 | Σпi = 100 |
Проверка: 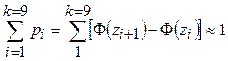 ;
; 
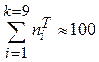 .
.
Проводим сопоставление эмпирических (по данным выборки) частот пi с полученными выравнивающими частотами (табл. 5).
Таблица 5
| пi | |||||||||
| пТi | 3,75 | 6,63 | 12,28 | 17,86 | 20,51 | 17,49 | 11,97 | 6,07 | 3,44 |
Объединяем малочисленные частоты (пi, пТi < 5) на левом и правом концах выборки с соседними интервалами и получаем окончательную таблицу с числом частичных интервалов S =7.
Таблица 6
| пi | |||||||
| пТi | 10,38 | 12,28 | 17,86 | 20,51 | 17,49 | 11,97 | 9,51 |
Проверяем согласие гипотезы о нормальном законе распределения изучаемой СВ Х по критерию Пирсона.
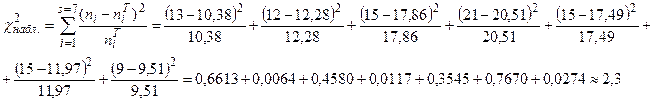
Число степеней свободы k=s –1– r = 7–1–2 = 4, где s − число интервалов, а k − число параметров нормального распределения. По таблице критических точек распределения χ 2 для уровня значимости α = 0,05 находим: χ 2 кр = 9,5 (см. табл. 3 приложения).
Так как χ 2набл.< χ 2кр, следовательно, гипотеза о нормальном законе распределения СВ Х принимается.
7. На гистограмме относительных частот (рис. 2) построим линию теоретической плотности нормального закона распределения 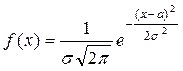 .
.
В рассматриваемом случае полагаем 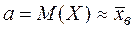 , σ ≈ σв.
, σ ≈ σв.
Тогда формула для плотности вероятности принимает вид:
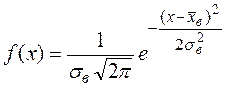 .
.
Найдем максимум функции f (x) и значения функции в точках перегиба:
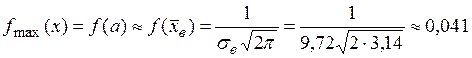 ,
,
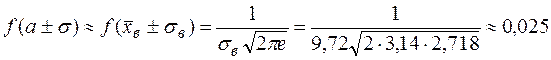 .
.
Выберем на оси х на участке гистограммы еще несколько точек, в качестве которых
удобно выбрать точки с координатами 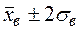 и
и 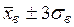 :
:
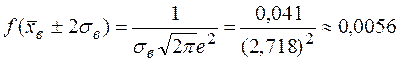 ;
;
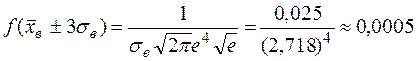 .
.
По полученным значениям f(x) на гистограмме относительных частот наносим линию теоретической плотности нормального распределения (на рис. 2 расчетные точки показаны кружками).
8. Находим доверительный интервал для оценки неизвестного математического ожидания СВ Х.
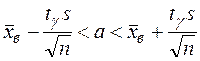 ,
,
где 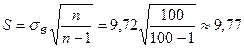 , γ = 0,95 (по условию задачи);
, γ = 0,95 (по условию задачи);
tγ = t (γ, n) = t (0,95; 100) = 1,984, (см. табл. 4 приложения)
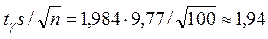 .
.
65,80 – 1,94 < a < 65,80 + 1,94, т.е. 63,86 < a < 66,74.
На основании проведенных расчетов можно сделать вывод о том, что с вероятностью γ = 0,95 неизвестное математическое ожидание СВ Х находится в интервале (63,86; 66,74).
Пример 13. Найти выборочное уравнение прямой регрессии У на Х: 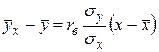 для двумерной случайной величины (Х, У), значения которой представленны в корреляционной таблице:
для двумерной случайной величины (Х, У), значения которой представленны в корреляционной таблице:
Таблица 7
 Х У Х У | пу | |||||
| - | - | - | ||||
| - | ||||||
| - | - | |||||
| пх |
Построить график линии регрессии на корреляционном поле. При проверке значимости коэффициента корреляции принять доверительную вероятность γ = 0,95.
1. Используя данные корреляционной таблицы определяем 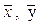 , σ 2 х, σ 2 у, σх, σ у, сху, rв.
, σ 2 х, σ 2 у, σх, σ у, сху, rв.
Предварительно вычислим суммы:
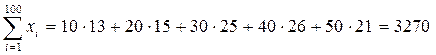 ;
;
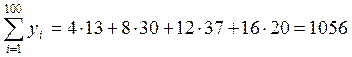 ;
;
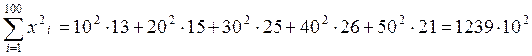 ;
;
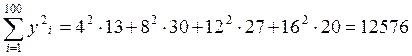 ;
;
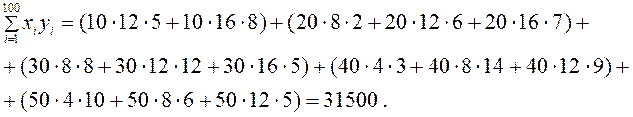
Средние арифметические значения:
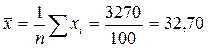 ;
; 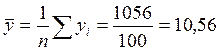 .
.
Дисперсия и средние квадратические отклонения:
D(X) = 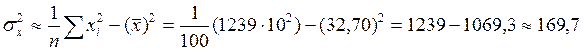 ;
;
D(Y) = 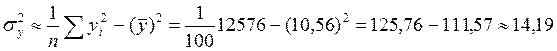 ;
;
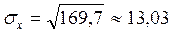 ;
; 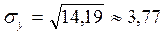 .
.
Корреляционный момент
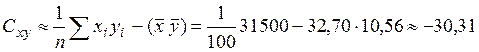 .
.
Выборочный коэффициент корреляции 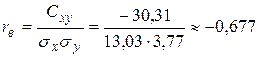 .
.
2. Приняв доверительную вероятность γ = 0,95 при п = 100 и числе степеней свободы k = n – 2 = 98 по таблице распределения Стьюдента (см. табл. 4 приложения) определяем значение
tкр = t 0,95; 98 ≈ 1,99.
Вычисляем статистику 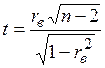 .
.
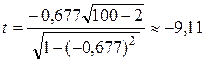 ;
; 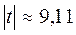 .
.
Так как 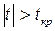 , то гипотезу об отсутствии линейной корреляции между СВ Х и У отвергаем.
, то гипотезу об отсутствии линейной корреляции между СВ Х и У отвергаем.
3. Находим уравнение линии эмпирической регрессии:
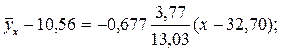
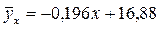 .
.
4. В системе координат х и у, используя корреляционную таблицу, соответствующими точками изображаем корреляционное поле и наносим прямую выборочной регрессии согласно полученного уравнения. На корреляционное поле (рис. 3) цифрами показано количество совпадающих точек. Положение прямой линии регрессии 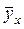 соответствует расположению экспериментальных точек.
соответствует расположению экспериментальных точек.
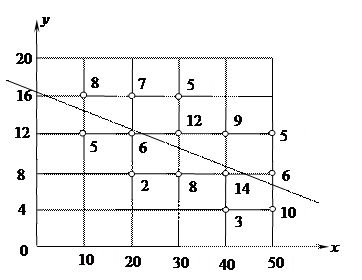
Рис. 6
ПРИЛОЖЕНИЕ
Таблица 1
Таблица значений функции 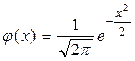 ,
, 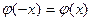
| х | ||||||||||
| 0,0 | 0,3989 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | 0,2420 | |||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | 0,0540 | |||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 |
| х | |||||||||||||
| 2,5 | |||||||||||||
| 2,6 | |||||||||||||
| 2,7 | |||||||||||||
| 2,8 | |||||||||||||
| 2,9 | |||||||||||||
| 3,0 | 0,0044 | ||||||||||||
| 3,1 | |||||||||||||
| 3,2 | |||||||||||||
| 3,3 | |||||||||||||
| 3,4 | |||||||||||||
| 3,5 | |||||||||||||
| 3,6 | |||||||||||||
| 3,7 | |||||||||||||
| 3,8 | |||||||||||||
| 3,9 | |||||||||||||
Таблица 2
Таблица значений функции 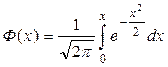 ,
, 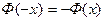
| х | ||||||||||
| 0,0 | 0,00000 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | ||||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | 0,49865 | 3,1 | 3,2 | 3,3 | 3,4 | |||||
| 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | ||||||
| 4,0 | ||||||||||
| 4,5 | ||||||||||
| 5,0 | ||||||||||
Таблица 4 Таблица 3
Таблица значений tγ = t (γ, n) Критические точки распределения χ2
| n\γ | 0,95 | n\γ | 0,95 | Число степеней свободы k | Уровень значимости 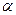 | ||
| 2,78 | 2,093 | 0,01 | 0,05 | ||||
| 2,57 | 2,064 | ||||||
| 2,45 | 2,045 | 6,6 | 3,8 | ||||
| 2,37 | 2,032 | 9,2 | 6,0 | ||||
| 2,31 | 2,023 | 11,3 | 7,8 | ||||
| 2,26 | 2,016 | 13,3 | 9,5 | ||||
| 2,23 | 2,009 | 15,1 | 11,1 | ||||
| 2,20 | 2,001 | 16,8 | 12,6 | ||||
| 2,18 | 1,996 | 18,5 | 14,1 | ||||
| 2,16 | 1,001 | 20,1 | 15,5 | ||||
| 2,15 | 1,987 | 21,7 | 16,9 | ||||
| 2,13 | 1,984 | 23,2 | 18,3 | ||||
| 2,12 | 1,980 | 24,7 | 19,7 | ||||
| 2,11 | ∞ | 1,960 | 26,2 | 21,0 | |||
| 2,10 | 27,7 | 22,4 | |||||
| 29,1 | 23,7 | ||||||
| 30,6 | 25,0 | ||||||
| 32,0 | 26,3 | ||||||
| 33,4 | 27,6 | ||||||
| 34,8 | 28,9 | ||||||
| 36,2 | 30,1 | ||||||
| 37,6 | 31,4 |
 2015-03-07
2015-03-07 3096
3096
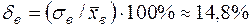 .
.