Статистическая устойчивость

 

В последовательности экспериментов со случайным исходом невозможно точно предсказать результаты отдельных опытов, так как в этих результатах обнаруживаются нерегулярные случайные колебания, не поддающиеся точному учету. Однако, если рассматривать последовательность в целом, а не отдельные результаты, то можно обнаружить чрезвычайно важное явление: несмотря на нерегулярное изменение результатов в отдельных опытах, средние результаты в достаточно длинной последовательности экспериментов со случайным исходом обнаруживают устойчивость.

Пусть в результате эксперимента  событие  может произойти или не произойти. Если выполнено  экспериментов , в которых событие  произошло 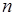 раз, то число

      (2.1)

называется частотой появления события .

Экспериментально установлено, что при увеличении  частота  имеет тенденцию сходиться к некоторому постоянному значению. Об этом экспериментальном факте говорят как об устойчивости частоты, или о статистической устойчивости. Однако, не следует думать, что всякий эксперимент со случайным исходом обладает свойством устойчивости частоты. В теории вероятностей речь идет только об экспериментах, обладающих этим свойством. В качестве иллюстрации свойства статистической устойчивости рассмотрим график зависимости частоты  появления герба при бросании монеты от числа  опытов, представленный на рис.2.1. Для построения этого графика выполнялось бросание монеты 30 раз, в каждом опыте фиксировался исход и вычислялась частота  по формуле (2.1), где  - число опытов, из которых в  опытах появился герб.

Рис. 2.1. График частоты появления герба как функции числа

бросаний монеты.

 

Естественно выдвинуть предположение о существовании предела,

,                       (2.2)

к которому стремится частота с увеличением числа  опытов. Однако, это предположение не может быть доказано или отвергнуто опытом. Но опыт подтверждает более слабое утверждение об устойчивости частоты появления события. Факт статистической устойчивости и является эмпирической основой теории вероятностей и математической статистики.

 

Понятие вероятности

 

Теория вероятностей - это математическая теория, которая дает описание экспериментов со случайными исходами, обладающих свойством статистической устойчивости. Теория вероятностей строится как аксиоматическая теория, то есть в ее основу положена система аксиом. В свою очередь аксиомы сформулированы на основе экспериментальных данных, а именно на свойствах частоты и, в частности, на факте статистической устойчивости, состоящем в тенденции частоты  появления события  стать постоянной и равной некоторому числу при большом числе повторений  эксперимента .

Таким образом, при построении теории необходимо ввести число  называемое вероятностью события , что реализуется с помощью одной из аксиом, которая называется аксиомой существования вероятности. Далее необходимо рассмотреть основные свойства частот и выразить эти свойства как утверждения относительно свойств вероятностей. Эти утверждения вместе с постулатом существования вероятности образуют систему аксиом теории вероятностей.

Частоту  можно рассматривать как результат измерения (оценивания) вероятности  по экспериментальным данным. Таким образом, равенство  означает, что при большом числе  опытов , а ошибка  имеет тенденцию снижаться с увеличением . Поскольку , то частота  появления события  в серии из  опытов удовлетворяет условию

 

.                                        (3.1)

Аналогичному условию должна удовлетворять и вероятность:

.                                       (3.2)

Рассмотрим значения вероятности на границах интервала . Пусть , тогда событие  называется невозможным и обозначается символом . Для невозможного события его частота  и имеет тенденцию приближаться к нулю с увеличением числа  опытов. Если , то событие  называется достоверным и обозначается символом . Частота достоверного события  и с увеличением числа опытов имеет тенденцию приближаться к единице.

 

Алгебра событий

 

Рассмотрим основные операции над событиями и понятие алгебры событий. Пусть  - некоторое событие.

1. Дополнением события  называется событие , состоящее в том, что событие  не произошло.

Операциям над событиями можно давать простую геометрическую интерпретацию. Рассмотрим такую интерпретацию операции дополнения. Пусть эксперимент состоит в случайном бросании точки на плоскость, при этом множество условий  таково, что исход каждого опыта – это попадание точки в область  плоскости, рис.4.1. Реализовать такой опыт можно,

 

 

Рис. 4.1. Событие  и его дополнение .

 

бросая шарик радиуса  в сосуд с плоским дном. При этом область  – это та часть дна сосуда, в которую может попасть центр шарика, то есть области  не принадлежит только полоса шириной  около стенки сосуда. Пусть  – подобласть области . Множества  и  точек плоскости можно рассматривать как события:  – событие, состоящее в том, что случайно брошенная на плоскость точка попадет в область ; и событие  – это попадание точки в область . По условию событие  появляется в каждом опыте, его вероятность , следовательно,  – достоверное событие. По определению  – это событие, состоящее в том, что  не произошло. Поэтому в данной интерпретации  – это непопадание точки в область , то есть  – попадание точки в заштрихованную область, рис.4.1.

2. Объединением (или суммой) двух событий  и  называется третье событие , состоящее в том, что произошло хотя бы одно из событий  или . Для объединения будем использовать обозначение

или  .                                          (4.1)

Признаком операции объединения двух событий может служить союз "или" между ними. Операции объединения, аналогично дополнению, можно дать геометрическую интерпретацию. Пусть  – событие, состоящее в том, что случайно брошенная на плоскость точка попала в область, обозначенную также , рис. 4.2. Аналогично событие  – это попадание точки в область

Рис. 4.2. События ,  и их объединение .

 

. Тогда событие  – это попадание точки в заштрихованную область, рис. 4.2.

Операция объединения определяется для произвольного числа событий. Например, событие

                                    (4.2)

состоит в том, что происходит хотя бы одно из событий , …. Событие

                                             (4.3)

состоит в том, что происходит хотя бы одно из событий … . Очевидно операция объединения коммутативна по определению:

                                     (4.4)

и ассоциативна, что также следует из определения:

.                          (4.5)

 

3. Пересечением (или произведением) двух событий  и  называется третье событие , состоящее в том, что произошли оба события  и . Для обозначения операции пересечения будем использовать обозначения

или .                            (4.6)

Геометрическая интерпретация операции пересечения представлена на рис. 4.3., где  и – события и  – их пересечение – заштрихованная область.

Операция пересечения, также как и операция объединения, определяется для произвольного числа событий. Например, событие

                                    (4.7)

состоит в том, что происходят все события  Событие

                                             (4.8)

состоит в том, что происходят все события

.                                             (4.9)

По определению операция пересечения коммутативна, то есть выполняется условие:

,                                             (4.10)

а также ассоциативна:

.                          (4.11)

Рис. 4.3. События ,  и их пересечение .

Операции объединения  и пересечения  взаимно дистрибутивны. В частности, операция объединения дистрибутивна относительно пересечения:

.               (4.12)

На рис. 4.4,а представлены события горизонтальной штриховкой и вся левая часть (4.12) – вертикальной штриховкой. Аналогично на рис. 4.4, б представлены: событие  – горизонтальной штриховкой, событие  – вертикальной штриховкой, вся правая часть (4.12) – штриховкой "в клеточку".

                                 а                               б

Рис. 4.4. Геометрическая иллюстрация дистрибутивности объединения относительно пересечения.

Аналогично (4.12) операция пересечения дистрибутивна относительно

объединения:

.                 (4.13)

На рис. 4.5, а представлены: событие – горизонтальной штриховкой и левая часть соотношения (4.13) – штриховкой "в клеточку". На рис. 4.5,б: событие  – горизонтальной штриховкой, событие – вертикальной штриховкой и вся правая часть (4.13) – это вся заштрихованная область.

              а                               б

Рис. 4.5. Геометрическая иллюстрация дистрибутивности пересечения относительно объединения.

 

Отметим, что если в (4.13) для операции объединения использовать знак "+", а для пересечения – отсутствие знака, то (4.13) принимает хорошо знакомый вид:

                                (4.14)

– закона дистрибутивности умножения относительно сложения в алгебре чисел. В отличие от этого закон дистрибутивности (4.12) сложения относительно умножения не имеет аналога в алгебре чисел.

 

4. Рассмотренные операции над событиями носят алгебраический характер. Поэтому в теории вероятностей важное значение имеет алгебра событий, которая определяется следующим образом.

Система событий  называется алгеброй событий, если для любой пары событий  и  из условий

                                       (4.15)

следует, что события , , ,  содержатся в .

Говорят, что алгебра событий – это система событий, замкнутая относительно операций дополнения, пересечения и объединения.