Сопоставление результатов финансового анализа с критериями отбора проектов в портфель

Результаты проведения финансового анализа являются основой принятия окончательных решений о включении инвестиционных проектов в портфель. Сравнивая полученные в ходе финансового анализа результаты с заранее определенными критериями отбора проектов в портфель, принимается инвестиционное решение. Крите­рии отбора каждое предприятие устанавливает для себя произвольно, исходя из конкретных условий производственной и инвестиционной деятельности. В основе выбора критерия могут лежать такие признаки, как классификационная категория, к которой отнесены проекты; тип используемого финансового анализа; длительность проектов; эффек­тивность (доходность) и ликвидность проектов; степень их важности для предприятия; стоимость капитала для финансирования проектов и уровень их риска и т.д.

Большое значение для установления критерия имеет правиль­ный выбор нужного показателя и точное определение его порогового значения, являющегося для предприятия мерой оценки капитальных вложений. Основная проблема при отборе инвестиционных проек­тов в портфель заключается в противоречивости этих показателей. Даже при принятии решения в отношении единичного проекта могут возникнуть диаметрально противоположные выводы о приемлемо­сти инвестиций, основанные на том, какой показатель взят за основу. Очевидно, что если речь идет о портфеле, в котором могут быть как независимые, так и конкурирующие проекты, противоречия неиз­бежны.

Критерии, основанные на бухгалтерском подходе к финансовой оценке капитальных вложений (на значении показателей РР и ARR), являются в большей степени независимыми друг от друга: РР полезен в качестве метода, применяемого на этапе первичной оценки и отбора проектов, ARR имеет некоторые преимущества, облегчая сравнение инвестиционных затрат и будущих доходов. Если установление критериев приемлемости и финансовый анализ производятся одним и тем же методом, инвестиционные решения, принятые на их основе, раз­личаться не будут. Тем не менее предприятия могут устанавливать различные пороговые значения этих критериев, поэтому возможность возникновения противоречий не исключена.

Взаимосвязи между критериями, основанными на экономиче­ском (финансовом) подходе к анализу и оценке капитальных вложе­ний, намного сложнее. Если в портфель объединяются независимые проекты, то противоречий между рассчитываемыми показателями NPV, Pin IRR, как правило, не возникает. Все они дают одинаковые результаты относительно принятия инвестиционного решения. Вза­имосвязь между критериями очевидна:

если NPV > О, одновременно IRR > СС и PI > 1;

если NPV < 0, одновременно IRR < СС и PI < 1;

если NPV= 0, одновременно IRR = СС и PI = 1.

Если в портфель объединяются помимо независимых еще и кон­курирующие, взаимоисключающие проекты, то противоречия неиз­бежны. Инвестиционные проекты могут конкурировать между собой в силу того, что они являются взаимоисключающими. Обычно взаи­моисключающими оказываются инвестиции, которые обеспечивают альтернативные способы достижения одного и того же результата или использование какого-либо ограниченного ресурса (только не денеж­ных средств). Ограниченность финансовых ресурсов также делает невозможным включение в портфель одновременно всех приемле­мых инвестиционных проектов и некоторые из них приходится либо отвергать, либо откладывать на будущее. В подобных ситуациях фор­мирование портфеля требует ранжирования проектов по степени их приоритетности (независимо от того, являются они независимыми или взаимоисключающими), а затем отбора в зависимости от ис­пользуемого критерия.

Каждый из существующих критериев отбора проектов в порт­фель имеет свои преимущества и недостатки.

Исследования, проведенные крупнейшими учеными и специа­листами в области финансового менеджмента, показали, что в случае противоречия критериев предпочтение следует отдавать критерию, основанному на значениях показателя NPV. При определении NPV не приходится сталкиваться с вычислительными проблемами, как при расчете IRR. Показатель NPV позволяет определить стоимость, которую имеют капитальные вложения для инвестора, он дает вероятностную оценку прироста стоимости предприятия, в полной мере отвечает основной цели предприятия (наращивание экономического потен­циала и рост благосостояния предприятия и его акционеров), позво­ляет узнать, что может извлечь инвестор из конкретного проекта (так как взаимосвязь NPV и PI может свидетельствовать и о стоимости капитальных вложений и о привлекательности дохода, полученного от конкретной суммы вложенных средств), наконец, позволяет учи­тывать кумулятивность поступлений от проекта и использовать агре­гированную величину для оптимизации портфеля.

Несмотря на то, что по многим сравнительным параметрам при­оритет отдается NPV, практики часто предпочитают критерий, осно­ванный на значениях показателя IRR (у менеджеров американских компаний соотношение предпочтений в пользу критерия IRR —3:1) Это объясняется относительностью показателя IRR, на основе кото­рого легче принимать решение, тогда как NPV является, как известно, абсолютным показателем.

Особенности критериев отбора проектов в портфель и проблемы их применения необходимо охарактеризовать детальнее.

В сравнительном анализе альтернативных, взаимоисключающих проектов критерий IRR дает оценку, которая не всегда совпадает с ре­зультатами анализа NPV, поэтому может использоваться достаточно условно. В подобных ситуациях метод IRR может быть скорректиро­ван. При анализе исходят из показателя IRR, рассчитанного из разницы денежных потоков каждого рассматриваемого проекта. Расчет IRR ведется для приростных показателей капитальных вложений и доходов по проекту. Если при этом IRR > СС, приростные показатели оправданы и целесообразно принять проект с более низким значением IRR.

Нахождение IRR для приростного денежного потока связано с опре­делением точки Фишера, показывающей значение коэффициента дисконтирования, при котором рассматриваемые проекты имеют одинаковый NPV. Она служит пограничной точкой, разделяющей ситуации, определяемые критерием NPVm не определяемые крите­рием IRR. Если значение цены капитала находится за пределами численного значения точки Фишера, рассчитываемые показатели NPV и IRR дают одинаковые результаты при оценке альтернативных про­ектов. Если цена капитала меньше численного значения точки Фи­шера — NPV u IRR противоречат друг другу. Точка Фишера численно равна IRR приростного денежного потока, составленного из разно­стей соответствующих элементов исходных потоков.

Для стандартных, единичных проектов критерий IRR показывает лишь максимальный уровень затрат, допустимый для оцениваемого проекта. Если цена капитала, привлекаемого для финансирования альтернативных проектов/меньше значения IRR для них, выбор может быть сделан лишь с помощью дополнительных критериев.

Недостатком критерия IRR является невозможность с его помощью различать ситуации, когда цена капитала меняется. Расчет показа­теля IRR предполагает, что ставка дисконтирования будет постоян­ной во время всего срока жизни проекта. Если изменения ставки можно предсказать, то NPV проекта легко просчитывается путем при­ведения денежных потоков каждого года по соответствующей каждому году ставке дисконтирования.

Критерий IRR совершенно непригоден для анализа инвестици­онных проектов с неординарными денежными потоками. В этих слу­чаях возникает множественность (или отсутствие вовсе) значений IRR и неочевидность экономической интерпретации возникающих соот­ношений между IRR и ценой капитала. Графическое изображение связи между IRR и NPV приведено на рис. 2.

NPV

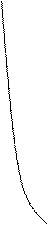B

IRR IRR

IRR i

IRR

А Б

Рис. 2. График NPV проектов

Случай А является типичным проектом с ординарными денежными потоками. Кривая только один раз пересекает ось абсцисс в точке, соответствующей численному значению IRR. В случае Б денежные потоки неординарные, оттоки и притоки капитала чередуются, гра­фик меняет траекторию и несколько раз пересекает ось абсцисс — возникает несколько значений IRR. Случай В вообще не имеет IRR.

Данный недостаток, присущий IRR, в отношении оценки проектов с неординарными денежными потоками, не является критическим. Аналогом IRR, который может применяться при анализе любых про­ектов, является показатель модифицированной внутренней нормы прибыли (MIRR). Для ее определения сначала рассчитывается сум­марная дисконтированная стоимость всех оттоков денежных средств (OF) и суммарная наращенная стоимость всех притоков денежных средств (IF), причем и дисконтирование и наращение осуществляются по цене источника финансирования проекта. Наращенная стоимость притоков называется терминальной стоимостью. Далее определяется коэффициент дисконтирования, уравнивающий суммарную приве­денную стоимость оттоков и терминальную стоимость. Данный ко­эффициент дисконтирования и будет MIRR.

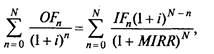
где OF_n — отток денежных средств в n -м периоде;

IF_n — приток денежных средств в n-м периоде.

Формула имеет смысл, если терминальная стоимость превышает сумму дисконтированных оттоков.

Критерий MIRR, основанный на значениях показателя MIRR, характеризующий эффективность проекта и применяемый вместо критерия IRR, всегда имеет единственное значение, в полной мере согласуется с критерием NPV и может использоваться для оценки независимых проектов. Для альтернативных проектов противоречия между критериями NPV и MIRR могут возникать, если проекты несо­измеримы по масштабу либо имеют разную продолжительность. В этом случае рекомендуется применять критерий NPV.

Еще одна проблема метода IRR обусловлена допущением о ре­инвестициях. Модель расчета IRR предполагает, что все денежные потоки от осуществления проекта могут быть реинвестированы по ставке IRR. Однако это не реально. Реинвестирование денежных потоков от капитальных вложений будет происходить по сложившейся на рынке инвестиционной процентной ставке, или по ставке дисконтирования, или в соответствии со стоимостью капитала. Поэтому метод IRR преувеличивает доход, который может быть получен от ин­вестиций. При методе NPV подобных допущений не бывает. Возмож­ность изменять ставку дисконтирования при расчетах, чтобы учесть» изменяющиеся инвестиционные условия, делает метод NPV предпочтительнее.

Безусловно, ориентация на единственный критерий IRR также не всегда оправдана. Основной его недостаток в том, что это абсолютный показатель, который не дает информации о резерве безопасности проекта. Любая серьезная погрешность или ошибка в прогнозе денежного потока, в выборе ставки дисконтирования таит опасность, того, что проект, который ранее рассматривался как прибыльный, окажется убыточным.

Информацию о резерве безопасности проекта дают критерии IRR и PI. При прочих равных условиях, чем больше IRR по сравнениию с ценой капитала, тем больше резерв безопасности. Чем больше значение PI превосходит единицу, тем больше резерв безопасности, С позиции риска можно сравнивать проекты по критериям IRR и PI но нельзя — по критерию NPV.

Высокое значение также NPV не может служить решающим аргументом при принятии решений, так как оно, во-первых, определяется масштабом проекта, а во-вторых, может быть сопряжено с достаточно высоким риском и степень риска, присущая этому значение NPV, не ясна.

При расчете NPV применении его как критерия отбора инвестиционных проектов в портфель существует ряд практических аспектов, которые обязательно должны учитываться: следует принимать во внимание действие налогов, норм амортизации, а также инфляцию.

Нельзя правильно оценить инвестиционный проект и сделать вывод о его включении в портфель, не принимая во внимание вопросы налогообложения. Налоги влияют на значение показателя NPV проектов, изменяя их денежные потоки. Это происходит потому, что реальные денежные поступления, связанные с осуществлением проекта (доходы и затраты), и амортизация основных фондов, занятых в проекте, оказывают влияние на отчетную прибыль и поэтому изменяют налогооблагаемую базу.

На стоимость денежных потоков влияет также инфляция. Она обычно учитывается в ставке дисконтирования, которая используется при оценке проектов.

Норма прибыли, включающая в себя инфляцию, называется номинальной ставкой. Реальная ставка (т.е. без инфляции) показывает, какую реальную прибыль получит инвестор после учета влияния инфляции. Связь между реальной и номинальной ставками (нормой прибыли) можно выразить формулами:

и

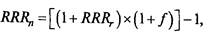
где RRR_r — реальная норма прибыли (ставка);

RRR_n — номинальная норма прибыли (ставка);

f — уровень инфляции.

При расчете NPV инвестиционных проектов важно, чтобы обе ставки (реальная и номинальная) и денежные потоки соответствова­ли друг другу. Если в качестве ставки дисконтирования используется RRR_n, инфляция увеличивает номинальный объем денежных пото­ков за срок жизни инвестиционного проекта. Если предполагается, что денежные потоки останутся постоянными в течение срока жизни проекта, следует использовать RRR_r. На практике весьма распростра­нена ошибка, когда используют несовместимые комбинации RRR и денежных потоков, что приводит к неверной оценке NPV.

Метод NPV позволяет принимать правильное решение при срав­нительном анализе отбираемых в портфель проектов, имеющих раз­ные сроки жизни. Существуют специальные методы, позволяющие устранить временную несопоставимость (влияние временного фак­тора), чтобы корректно сравнить их.

1. Метод цепного повтора в рамках общего срока действия про­ектов — нахождение наименьшего общего кратного сроков действия проектов и предположение, что краткосрочный проект самовозобнов­ляется после своего завершения. Последовательность действий в данном методе следующая:

• находят наименьшее общее кратное сроков действия анализи­руемых проектов;

• рассчитывают с учетом фактора времени суммарный NPV пpoектов, реализуемых необходимое число раз в течение сроков действия проектов, рассматривая каждый проект как повторяющийся;

• выбирают тот проект, для которого суммарный NPV повторя­ющегося потока имеет наибольшее значение.

Данный метод наиболее приемлем, если сроки действия рассматриваемых проектов кратны друг другу.

Однако на практике не редки ситуации, когда инвестиционные ресурсы могут быть реинвестированы бесконечно. Чтобы обеспечить сопоставимость и корректность расчетов для отдаленного во време­ни периода, когда созданные в результате инвестирования активы достигнут конца своей эксплуатации, необходимо выполнить доста­точно сложные вычисления. В таких случаях применяют удобный инструмент упрощения расчетов — эквивалентный аннуитет.

2. Метод определения эквивалентного аннуитета — стандартного, унифицированного аннуитета, который имеет ту же продолжитель­ность, что и оцениваемый инвестиционный проект, и ту же величину текущей стоимости, что и NPV этого проекта. Последовательность действий в данном методе следующая:

• рассчитывают NPV однократной реализации каждого проекта;

• находят для каждого проекта эквивалентный срочный аннуитет, приведенная стоимость которого в точности равна NPV проекта;

• рассчитывают приведенную стоимость бессрочного аннуитета, предполагая, что найденный аннуитет может быть заменен бессроч­ным аннуитетом с той же самой величиной аннуитетного платежа;

• выбирают проект, имеющий максимальное значение бессроч­ного аннуитета.

Эквивалентный аннуитет (ЕА) рассчитывается по формуле

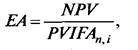
где PVIFA_n,i — текущая стоимость аннуитета ценой в 1 руб. в конце

каждого из п периодов при ставке i

Логика использования эквивалентного аннуитета состоит в том, что если такие аннуитеты определить для всех сравниваемых проек­тов, то проект, у которого ЕА будет наибольшим, будет обеспечивать наибольшую величину NPV всех денежных поступлений в условиях, когда все конкурирующие инвестиции будут предполагать бесконечное реинвестирование или реинвестирование до тех пор, пока сроки жизни всех проектов не завершатся одновременно.

Метод эквивалентного аннуитета технически является самым правильным и обычно легок в применении, так как позволяет исполь­зовать для расчетов финансовые таблицы и финансовые калькуляторы. Использование такого метода допустимо в случаях, когда сопостав­ляемые проекты имеют один и тот же уровень риска.

3. Метод, основанный на предположении, что долгосрочный про­ект продается до его завершения. Этот метод применяют, если проекты достаточно долгосрочны. Алгоритм метода следующий:

• предполагают, что долгосрочный проект продается в тот момент времени (обычно год), когда заканчивается краткосрочный проект;

• оценивают конечную (продажную) стоимость долгосрочного проекта на момент продажи (срок окончания краткосрочного проекта);

• рассчитывают NPV долгосрочного проекта;

• выбирают проект, имеющий большее значение NPV.