Процесс накопления капитала в динамике

Совершенно очевидно, что инвестиция на условиях простого процента менее выгодна, чем на условиях сложного процента, поскольку

rⁿ>rn при любом значении п > 1.

При размещении средств на условиях простого процента доходы по мере их начисления целесообразно снимать для потребления или использования в других инвестиционных проектах или текущей деятельности.

В инвестиционном анализе под стандартным временным интер­валом принято рассматривать один год. В случае же, когда дополни­тельно оговаривается частота начисления процентов по вложенным средствам в течение года, формула расчета будующей стоимости денег может иметь следующий вид:

FV_n =PV (1 + r / m)^nm, 3.7

где r — годовая процентная ставка (коэффициент);

т — количество начислений в году, ед.;

п — срок вложения денежных средств, лет.

Начисление процентов (дивидендов и других видов доходов) может осуществляться один раз в год, один раз в полугодие, поквар­тально, ежемесячно, ежедневно. Характерно, что чем большее количе­ство раз в течение года будут начисляться проценты, тем большую вели­чину составит будущая стоимость накопленной суммы в конце n -го периода.

Пример. Если вклад в сумме 1000 денежных ед. хранить в банке два года, то при годовой ставке 24% в зависимости от частоты начисления про­центов накопленная сумма вклада составит:

а) при начислении процента один раз в год

1000 (1 + 0,24)² = 1537,6 (ден. ед.);

б) при полугодовом начислении процентов

1000 (1+ 0,24: 2)²*² = 1573,5 (ден. ед.);

в) при ежеквартальном начислении процентов

1000 (1 + 0,24: 4)²*⁴ = 1593,8 (ден. ед.);

г) при ежемесячном начислении процентов

1000 (1 + 0,24:12)²* ¹² = 1608,1 (ден. ед.).

В ходе анализа эффективности нескольких инвестиционных про­ектов с различными интервалами наращения капитала необходимо использовать обобщающий финансовый показатель, позволяющий осуществлять их сравнительную оценку. Таким показателем является эффективная годовая процентная ставка (EAR), которая обеспечива­ет переход от PV к FV при заданных значениях их величин. Этот темп прироста капитала является универсальным для любой системы начис­лений и рассчитывается по формуле:

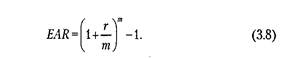
Пример. Предприятие может разместить свободные денежные сред­ства под 36% годовых при ежемесячном начислении процентов или под 38% годовых при условии начисления процентов дважды в год. Какой из вариантов размещения более выгоден для предприятия?

По первой схеме наращения капитала годовой темп прироста вложен­ной суммы составит EAR = (1 + 0,36: 12)¹² - 1 = 0,426 = 42,6 (%).

По второй схеме наращения первоначальный капитал будет ежегод­но увеличиваться на EAR = (1 + 0,38: 2)² - 1 = 0,416 = 41,6 (%).

Очевидно, что во втором случае накопленная сумма будет меньше, несмотря на то, что объявленная процентная ставка выше, чем при пер­вом варианте размещения.

8.5. Расчет текущей стоимости денежных средств в настоящем перио­де времени производится путем дисконтирования. Дисконтирование представляет собой процесс нахождения величины денежных средств на текущий момент времени по ее известному или предполагаемому значению в будущем, исходя из заданной процентной ставки.

Экономический смысл операции дисконтирования заключается во временном упорядочении денежных потоков, относящихся к раз­личным периодам времени. Коэффициент дисконтирования показы­вает, какой процент возврата хочет или может иметь инвестор на вкла­дываемую им сумму. В этом случае величина PV показывает текущую («сегодняшнюю», современную или приведенную) стоимость будущей величины FV денежных средств.

Функция дисконтирования является обратной по отношению к функции начисления сложного процента и выглядит так:

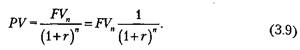
Отношение 1: (1 + r)ⁿ в инвестиционном анализе получило назва­ние коэффициента дисконтирования, а величина r называется нормой дисконта.

Пример. Какую сумму необходимо поместить на депозит под 10% годовых, чтобы через пять лет накопить 1500 тыс. ден. ед.?

При ответе на вопросы подобного рода необходимо рассчитать при­веденную (текущую) стоимость будущего дохода:

PV = 1500: (1 + 0,10)⁵ = 931,4 (тыс. ден. ед.).

Таким образом, инвестирование 931,4 тыс. ден. ед. на срок пять лет при ставке доходности 10% обеспечит накопление в сумме 1500 тыс. ден. ед.

Специфика инвестиционных проектов состоит в том, что они пред­полагают не отдельные или единовременные платежи (как доходы, так и расходы), а некоторую их последовательность во времени. Такие последовательности, или ряды платежей, называются денежными пото­ками (cash flows — CF), а отдельный элемент этого ряда — членом потока.

Для оценки эффективности инвестиций, планирования погаше­ния задолженности, сравнения эффективности коммерческих контрак­тов и т.п. необходимо оперировать сопоставимыми (с точки зрения временной концепции стоимости денег) величинами денежных пото­ков доходов и денежных потоков затрат. Для этого финансовый анализ предполагает расчет одной из двух обобщающих характеристик денеж­ного потока: наращенной суммы и современной стоимости суммарно­го денежного потока.

Наращенная сумма (amount of cash flows) — сумма всех членов денежного потока с начисленными на них к концу срока процентами. Под современной, или текущей, стоимостью денежного потока (present value of cash flows) понимают сумму всех его членов, дисконтирован­ных на начало горизонта расчета.

Пример. Фирме предложено инвестировать 100 тыс. ден. ед. на срок 5 лет при условии возврата в конце каждого года по 20 тыс. ден. ед. и выплате дополнительного вознаграждения в конце пятого года в раз­мере 30 тыс. ден. ед. Стоит ли принимать это предложение, если свобод­ные денежные средства фирма в настоящее время размещает на банков­ском депозите под 12% годовых?

Первый подход. Все денежные потоки доходов приводятся к момен­ту принятия решения (началу первого года), т.е. дисконтируются. После этого они становятся сопоставимыми как между собой, так и с суммой первоначальных вложений. Находится текущая стоимость денежного потока доходов по формуле:

где CF_i — денежный поток i -го шага расчета;

r — норма дисконта;

п — количество шагов в горизонте расчета;

PV — суммарный дисконтированный денежный поток, порожденный инвестированием.

Затем текущая стоимость денежных потоков доходов сравнивается с величиной первоначальных вложений. В качестве нормы дисконта здесь необходимо использовать 12%, поскольку это тот уровень доходности, который фирма может получить от альтернативного варианта размеще­ния свободных денежных средств. Схема приведения денежных потоков в сопоставимый вид путем дисконтирования представлена на рис.

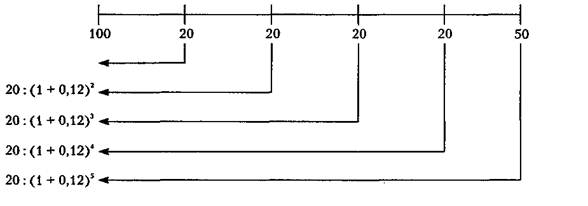
Схема расчета текущей стоимости денежного потока.

PV= 20: (1 + 0,12)¹ + 20: (1 + 0,12)² + 20: (1 + 0,12)³ + 20: (1 + 0,12)⁴+ +50: (1 + 0,12)⁵ = 17,86 + 15,94 + 14,24 + 12,72 + 28,35 = + 89,11 (тыс. ден. ед.).

Общая сумма всех денежных потоков доходов от предлагаемого вари­анта инвестирования, выраженная в текущей стоимости, оказалась мень­ше, чем та сумма денег, которую нужно вложить для получения этих дохо­дов. От такого инвестирования следует отказаться.

Второй подход. Можно для достижения сопоставимости доходов и вложений воспользоваться приведением всех денежных средств к кон­цу рассматриваемого периода времени (применить операцию наращения). В этом случае будущая сумма денежного потока находится по формуле

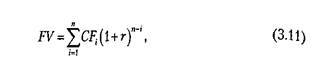
где CFi — денежный поток i-го шага расчета;

r — норма процента;

п — количество шагов в горизонте расчета;

FV — суммарный наращенный денежный поток, порожденный инве­стированием.

Эта величина покажет, какой суммой средств будет располагать фир­ма на конец пятого года, если все доходы, порожденные инвестировани­ем, по мере их поступления будут размещаться на депозитном вкладе под 12% годовых. Схема приведения денежных потоков в сопоставимый вид путем наращения представлена на рис.

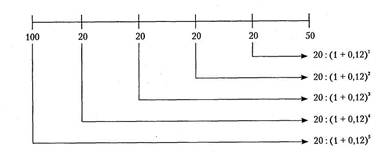
Схема расчета будущей стоимости денежного потока

FV= 20(1 + 0,12)⁴ + 20(1 + 0,12)³ + 20(1 + 0,12)² + 20(1 + 0Д2)¹ +

+ 50(1 + 0,12)° = 31,48 + 28,1 + 25,08 + 22,4 +50 = 157,06 (тыс. ден. ед.).

Если же фирма откажется от такого варианта инвестирования и раз­местит свободную сумму 100 тыс. ден. ед. на депозитном вкладе, то к концу пятого года накопленная величина вклада составит: FV- 100(1 + 0,12)⁵= 176,20 (тыс. ден. ед.).

Таким образом, от предложенного варианта инвестирования опять следует отказаться.

Иногда в инвестиционном анализе может быть применен и тре­тий подход к обеспечению сопоставимости разновременных денежных потоков. Он состоит в том, что все затраты и результаты приводятся к определенному моменту времени внутри рассматриваемого перио­да, который, будучи промежуточным, представляет интерес для инве­сторов и аналитиков. В качестве такого момента, например, может быть выбран момент начала эксплуатации будущего проектного решения. Формула для расчета суммы сопоставимых денежных потоков для этого варианта имеет вид

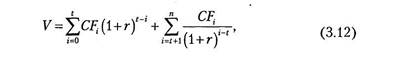
где r — норма процента (дисконта);

п — количество шагов в горизонте расчета;

t — период времени от начала горизонта расчета до момента, к кото­рому приводятся все денежные средства;

V — суммарный денежный поток, порожденный инвестированием, представленный в сопоставимом виде.

Схема приведения денежных потоков в сопоставимый вид по это­му алгоритму показана на рисунке:

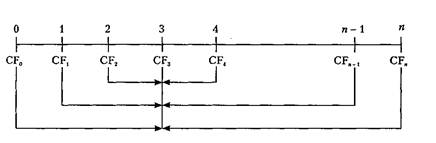
Схема приведения денежных потоков к промежуточному моменту

Приведение денежных потоков к одному временному моменту и по схеме наращения, и по схеме дисконтирования, и по смешанной схеме математически дает один и тот же результат при условии, что горизонт расчета один и тот же. Однако поскольку эффективность инвестиционного проекта анализируется постоянно в течение всего срока его жизни (на прединвестиционной стадии, на стадии осу­ществления вложении, на стадии эксплуатации), то может изменять­ся и сам горизонт расчета (увеличиваться прогнозный период по мере Продвижения вперед и получения новых данных), и количество шагов ^внутри него. В зависимости от целей анализа временные отрезки могут Как агрегироваться, так и разукрупняться (те денежные потоки, которые на прединвестиционной стадии прогнозировались в годовом исчис­лении, на стадии эксплуатации могут быть уточнены в помесячном или поквартальном разрезе).

В связи с этим в инвестиционном анализе в основном пользуются обратной задачей (т.е. дисконтированием, приведением всех величин к «сегодняшнему» моменту времени, каковым является момент нача­ла осуществления проекта или принятия решения по нему). Это свя­зано с необходимостью обеспечения независимости относительной ценности настоящих и будущих благ и показателей эффективности проекта от того, во сколько шагов производится их соизмерение.

8.6. Частными случаями расчета настоящей и будущей стоимости денег являются формулы на основе аннуитетной модели денежных потоков. Аннуитет представляет собой такой вид денежных потоков, при котором потоки осуществляются в равных размерах через равные периоды времени. Аннуитет может быть исходящим денежным пото­ком по отношению к инвестору (например, осуществление периоди­ческих равных процентных платежей по облигациям или банковским кредитам) или входящим денежным потоком (например, поступление арендной платы, которая обычно устанавливается одинаковой фикси­рованной суммой; получение депозитных процентов и др.).

Поступления и выбытия средств могут происходить в начале каж­дого конкретного периода (в этом случае имеет место предваритель­ный поток — пренумерандо) или в конце каждого периода (тогда говорят о последующем потоке — постнумерандо). Классическим аннуитетом считается модель на основе потоков постнумерандо (рав­ные платежи или поступления в конце каждого периода).

Будущая стоимость классического аннуитета, продолжающегося в течение п периодов, определяется по формуле

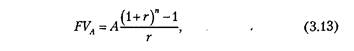
где FV_A — будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), ден. ед.;

А — член аннуитета, характеризующий размер отдельного платежа, ден. ед.

Порядок исчисления FV_A показан на рисунке: Расчет будущей стоимости классического аннуитета.

Пример. Какая сумма будет накоплена на счете, если в течение четы­рех лет в конце каждого года вносить 350 тыс. ден. ед., а банк начисляет по вкладам 6% годовых?

В данном случае необходимо рассчитать будущую стоимость класси­ческого аннуитета со сроком действия четыре года:

FV_A = 350 [(1 + 0,06)⁴- 1]: 0,06 = 1528 (тыс. ден. ед.)

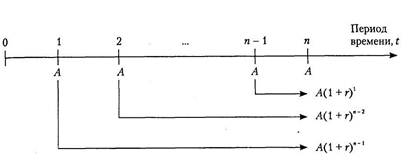
Схема расчета будущей стоимости классического аннуитета.

Текущая стоимость аннуитета равна сумме денежных средств, дис­контированных индивидуально по каждому периоду времени. Ее ве­личина в случае потока постнумерандо находится по формуле

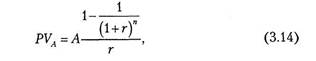
где PV_A — текущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), ден. ед.

Схема расчета текущей стоимости аннуитета, основанного на пото­ках постнумерандо, показана на рис. 3.8.

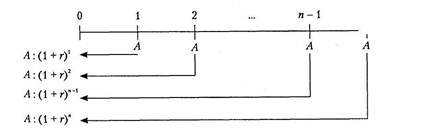
Схема расчета текущей стоимости классического аннуитета

Пример Какую сумму необходимо положить на депозит под 10% годо­вых, чтобы затем снимать по 300 тыс. ден. ед. в конце каждого года на про­тяжении пяти лет?

Рассчитаем текущую стоимость аннуитета, имеющего денежные пото­ки вида постнумерандо: PV_А = 300[(l - 1: (1+0,10)⁵]: 0,10 =1137 (тыс. ден.ед.)

Таким образом, разместив 1137 тыс. ден. ед. на депозитном вкладе под 10% годовых, инвестор будет иметь возможность снимать по 300 тыс ден. ед. пять лет подряд, или 1500 тыс. ден. ед. Разница между первона­чальным вкладом 1137 тыс. ден. ед. и накоплением 1500 ден. ед. обеспе­чивается суммой процентов, начисляемых на уменьшаемый остаток вкла­да по схеме сложного процента. Этот процесс предполагает в конечном счете нулевой остаток на депозите.

В практической деятельности коммерческих организаций возмож­на ситуация, когда поступления или оттоки денежных средств проис­ходят в начале каждого периода (например, лизинговые платежи). В таком случае речь идет об аннуитете, осуществляемом на основе пото­ков пренумерандо, иногда его называют авансовым аннуитетом. Для такой модели денежных потоков текущая и будущая стоимость аннуи­тета рассчитываются по формулам

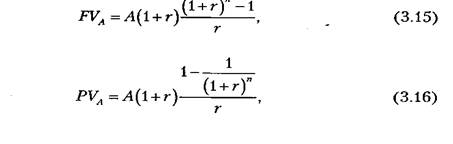
где: FV_A,PV_A – будущая и текущая стоимость аннуитета, осуществляемо­го на условиях предварительных платежей (пренумерандо), ден. ед.;

А – член аннуитета, характеризующий размер отдельного плате­жа, ден. ед.

Иногда возникает необходимость принятия решения о выгодно­сти приобретения аннуитета с необозримо долгим сроком получения денежных поступлений. Например, по договору страхования следует единовременно внести некую сумму на счет страховой компании, вза­мен чего (при наступлении страхового случая) страховщик ежегодно и пожизненно перечисляет застрахованному фиксированную сумму страховых выплат. В подобных случаях имеет место бессрочный аннуитет.

Постановка задачи с позиций будущей стоимости при бессрочном аннуитете не имеет смысла, а выгодность покупки такого аннуитета оценивается с помощью расчета текущей стоимости по формуле

где РV_А — текущая стоимость бессрочного (неопределенно длительного по времени) аннуитета, ден. ед.

В этом случае известен размер ежегодных поступлений, а в каче­стве нормы дисконта обычно принимается гарантированная процент­ная ставка (например, по банковскому депозиту).

В практике инвестиционного анализа могут возникать ситуации, когда известна не годовая процентная ставка, а ставка за меньший пери­од времени (месяц, квартал, полугодие и пр.). Переход к годовой вели­чине процентной ставки можно осуществить, основываясь на опреде­лении эффективной процентной ставки (EAR), по формуле

r = [(l + r_m)^m - l]100%, (3.18)

где r — годовая процентная ставка, %;

r_т — процентная ставка за подпериод т, %;

т — количество подпериодов в рамках периода (года).

Пример Недельный темп инфляции составляет 0,25%. Для прогно­зирования денежных потоков инвестиционного проекта необходимо определить текущую годовую ставку инфляции. Она будет равна i= [(1 + 0,0025)⁵²- 1]100% = 13,9 (%).

Если необходимо перейти от годовой нормы процента к норме по меньшему временному интервалу (установить процентную ставку за неделю, декаду, месяц и т.п.), можно воспользоваться обратной фор­мулой

Такое определение нормы дисконта необходимо при оценке эффективности инвестиционных проектов, поскольку при прогнози­ровании денежных потоков в течение расчетного периода использует­ся различная длительность шага расчета: первый год разбивается на месяцы, второй — на кварталы, третий — на полугодия, далее шаги принимаются равными одному году. В некоторых случаях, когда про­ект рассчитывается на длительный срок (например, более 20 лет), последние шаги могут составлять три-пять лет.

Все рассмотренные выше формулы позволяют привести разновре­менные денежные потоки в сопоставимый вид. Однако желательно учесть два в общем-то разных аспекта влияния фактора времени: нерав­ноценность разновременных эффектов и неравномерность денежного потока внутри шага.

При правильном разбиении расчетного периода всегда можно в общих чертах описать характер денежного потока на каждом шаге, выделив при этом доходы или расходы:

■ возникающие в начале шага;

■ возникающие в конце шага;

■ равномерно возникающие на протяжении шага.

Выводы

1. Во время резких изменений в экономике, технологии, экологии и политике выживание и успех в мире бизнеса в большей степени, чем когда-либо, зависят от правильности принимаемых решений. Инвестиционное решение — одна из наиболее важных деловых инициатив, которая должна осуществляться предпринимателями или менеджерами, поскольку инвестиции связывают финансовые ресурсы на относительно большой период времени. Инвестици­онное решение воплощается в инвестиционный проект.

2. Понятие «инвестиционный проект» можно трактовать по раз­ному: как дело, деятельность, мероприятие, предполагающее осу­ществление комплекса каких-либо действий, обеспечивающих достижение определенных целей; как систему организационно-правовых и расчетно-финансовых документов, необходимых для осуществления каких-либо действий или описывающих такие действия; как основной документ, устанавливающий необходимость осуществления реального инвестирования, в котором в определен­ной последовательности излагаются основные характеристики проекта и финансовые показатели, связанные с его реализацией.

3. Для инвестиционных проектов характерно интервальное про­текание процессов вложения ресурсов и получения в будущем потока доходов. В связи с этим важный момент при анализе инве­стиций — правильное определение расчетного периода или перио­да реализации проекта. Суммарная продолжительность прединвестиционной, инвестиционной и эксплуатационной фаз цикла составляет срок жизни проекта.

4. Для проведения анализа инвестиционного проекта расчетный период разбивается на шаги. Шагом расчетного периода называ­ется отрезок времени в расчетном периоде, для которого опреде­ляются технические, экономические и финансовые показатели проекта. Величина шага зависит от продолжительности различ­ных фаз жизненного цикла проекта. Расчетный период должен охватывать весь жизненный цикл инвестиционного проекта вплоть до его прекращения.

5. Все издержки, связанные с реализацией инвестиционного про­екта, можно разделить на три группы: первоначальные (предпроизводственные), текущие (затраты на производство инвестицион­ного продукта) и ликвидационные. Инвестиции следует четко отделять от затрат на производство (издержек фазы эксплуатации инвестиционного объекта). Особое значение имеет правильное определение величины чистых инвестиций.

6. Центральное место в анализе инвестиционных проектов зани­мает оценка будущих денежных потоков, возникающих в резуль­тате осуществления проекта. Чистый денежный поток, генериру­емый проектом в течение ряда временных периодов,— это чистое изменение от периода к периоду вызванных проектом денежных доходов и расходов. Расчет величины чистого денежного потока возможен с применением прямого и косвенного методов.

7. При оценке эффективности реальных инвестиций возникает задача обеспечения сопоставимости разновременных затрат и результатов, которая решается путем приведения стоимости де­нежных средств к одному моменту времени. Такое приведение воз­можно с применением операций дисконтирования или наращения капитала.

8. При расчете наращения и дисконтирования денежных потоков могут использоваться модели простых и сложных процентов. При последовательном осуществлении денежных потоков в равных размерах и через равные промежутки времени в инвестиционных расчетах используются формулы текущей и будущей стоимости аннуитета.

Контрольные вопросы

1. Дайте понятие инвестиционного проекта, рассмотрите фазы его разработки и классификацию инвестиционных проектов.

2. Что такое жизненный цикл инвестиционного проекта и какие факторы его определяют?

3. Выделите проблемы проведения достоверной оценки началь­ных инвестиционных затрат и предложите пути их решения.

4. Какова сущность косвенного и прямого методов оценки денеж­ного потока от операционной деятельности, в чем их разли­чия?

5. В чем причины несовпадения величины учетной прибыли и денежных потоков инвестиционного проекта?

6. Опишите последовательность расчета денежного потока на этапе разработки проекта и начального инвестирования.

7. Какова последовательность расчета денежного потока на эта­пе реализации (эксплуатации) проекта?

8. Как можно рассчитать денежный поток на этапе ликвидации (завершения) проекта?

9. В чем сущность временной концепции стоимости денег?

10. Дайте определение операций дисконтирования и наращения капитала. В чем состоит необходимость их применения при анализе инвестиционных проектов?

11. Что такое аннуитетная модель денежных поступлений и как рассчитывается текущая и будущая стоимость аннуитета?

12. Дайте определение понятия эффективной годовой процент­ной ставки. Каковы направления ее использования при анализе инвестиций?