ПО
МАТЕМАТИЧЕСКОЙ
СТАТИСТИКЕ
и варианты индивидуальных заданий
для выполнения расчётно-графических
работ
часть 1
г. Тюмень 2007
Предисловие
В сборнике содержатся методические указания и варианты лабораторной работы по теме: «Первичная обработка результатов наблюдения методом математической статистики. Оценка параметров «нормального» распределения».
Цель выполнения лабораторной работы – привить студентам навыки самостоятельной обработки эмпирически полученных данных с помощью основных методов математической статистики.
Методика сборника обеспечивает самостоятельное выполнение расчётно-графической работы.
Описание лабораторной работы включает краткие теоретические сведения и план выполнения работ:
· алгоритм вычисления;
· образец выполнения работы;
· контрольные вопросы;
· варианты заданий.
Лабораторный практикум содержит 50 вариантов и гарантирует индивидуальность его выполнения.
Наличие алгоритма позволяет все расчёты производить как в «ручном» режиме так и с помощью ЭВМ.
Рекомендуется для инженерных, экономических и агрономических специальностей.
Лабораторная работа №1
Первичная обработка результатов наблюдения методом математической статистики
Цель работы: Привить навыки первичной обработки эмпирических данных с помощью методов математической статистики.
Содержание работы:
1. Группировка данных в вариационный ряд и представление в виде эмпирической функции распределения.
2. Графическое изображение вариационного ряда и эмпирической функции распределения.
3. Вычисление основных числовых характеристик выборочной совокупности.
4. Определение границ истинных значений числовых характеристик, изучаемой случайной величины с заданной надёжностью.
5. Содержательная интерпретация результатов первичной обработки по условию задачи.
Форма отчета:
1. Представление работы по указанному в методике образцу.
2. Самостоятельное изучение теоретического материала с помощью предлагаемых контрольных вопросов.
3. Устное собеседование по работе, сдача зачета.
§ 1.1. Краткие теоретические сведения и план
выполнения работы.
Изучение свойств случайных величин методом математической статистики основано на первичной обработке результатов наблюдений, выраженных в числовой форме.
Целью первичной обработки является представление первичной числовой информации в более обозримой, сжатой форме, а также получение сведений об основных закономерностях изучаемой совокупности случайных величин.
В математической статистике различают генеральную совокупность и выборочную.
Под генеральной совокупностью понимается все мыслимое множество случайных объектов, обладающих общностью некоторого, изучаемого в данном исследовании, признака. Это множество, как правило, счетное.
Выборочная совокупность (выборка)- эта часть генеральной совокупности, которая фактически изучается.
Для того, чтобы по выборке можно было достаточно уверенно судить о свойствах генеральной совокупности она должна быть репрезентативной, т.е. достаточной по численности, случайной по отбору с соблюдением равной возможности каждого элемента генеральной совокупности попасть в выборку.
Теоретической основой выборочного метода является теорема Чебышева.
Теорема: с вероятностью, сколь угодно близкой к достоверности можно утверждать, что при достаточно большом числе наблюдений, ограниченной дисперсии генеральной совокупности попарно независимых случайных величин, разность между средним арифметическим и средним арифметическим их математических ожиданий будет сколь угодно малой, т.е.
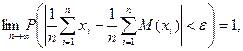
в частности 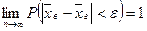 ,
,
где 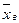 - средняя для выборочной совокупности;
- средняя для выборочной совокупности;
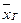 -средняя для генеральной совокупности;
-средняя для генеральной совокупности;
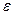 -как угодно малое положительное число.
-как угодно малое положительное число.
Итоги эмпирических наблюдений представляют собой простой статистический ряд- таблицу числовых значений изучаемой случайной величины. Известно, что, если находить числовые характеристики, предварительно сгруппировав полученные данные, то их значения будут ближе подходить к истинным значениям аналогичных характеристик генеральной совокупности.
Первичная обработка результатов наблюдений состоит из нескольких этапов. Рассмотрим содержание каждого из них.
Этап I. Группировка данных в вариационный ряд и представление его в виде функции распределения.
Для того, чтобы статистические данные представить в виде вариационного ряда с равноотстоящими вариантами необходимо:
1.В исходной таблице эмпирических данных найти наименьшее (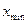 ) и наибольшее (
) и наибольшее (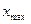 ) значения.
) значения.
2.Определить размах варьирования: 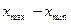
3. Наметить число интервалов группировки. Имея в виду, что выделением большого числа групп можно затушевать общую картину распределения, малое же число не позволит выявить характерную особенность изучаемой случайной величины. Исходя из опыта рекомендуется выделять от 5 до 20 групп так, чтобы каждая группа была достаточно наполнена значениями вариант. Можно также воспользоваться формулами:
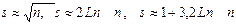
где s -число групп, n -объем выборки.
4. Определить длину интервала
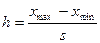 .
.
Если вычисленное отношение – число иррациональное, то его округляют до удобного целого значения.
5. Записать интервалы группировок и расположить их в порядке возрастания границ
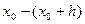 ,
, 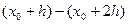 ,……….,
,………., 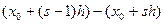 ,
,
где 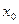 - нижняя граница первого интервала. За
- нижняя граница первого интервала. За 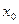 берется удобное “круглое” число не большее
берется удобное “круглое” число не большее 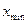 , верхняя граница последнего интервала должна быть не меньше
, верхняя граница последнего интервала должна быть не меньше 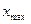 .Это делается для того, чтобы интервалы содержали в себе исходные значения случайной величины.
.Это делается для того, чтобы интервалы содержали в себе исходные значения случайной величины.
6. Разнести исходные данные по интервалам группировок, т.е. подсчитать по исходной таблице число значений случайной величины, попадающих в указанные интервалы. Если некоторые значения совпадают с границами интервалов, то их относят либо только к предыдущему, либо только к последующему интервалу.
Записать интервальный ряд частот и относительных частот.
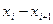 | 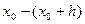 | 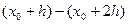 | … | 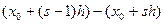 |
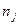 | 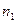 | 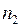 | … | 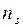 |
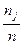 | 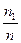 | 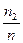 | … | 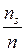 |
7. От интервального ряда перейти к дискретному. Для этого каждый интервал заменить его средним значением, оставив частоты и относительные частоты без изменения.
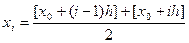
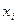 | 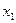 | 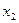 | … | 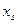 |
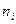 | 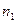 | 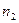 | … | 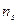 |
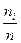 | 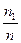 | 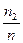 | … | 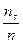 |
8. Записать эмпирическую функцию распределения.

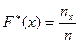
где 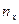 - число вариант, значения которых меньше чем
- число вариант, значения которых меньше чем 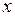 ;
;
n - число всех значений, объем выборки.
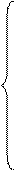


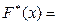


………………………..
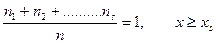
 F*(x) определяет относительную частоту события (X<x).
F*(x) определяет относительную частоту события (X<x).
Замечание №1. Интервалы необязательно брать равными по длине. На участках, где значения располагаются гуще, удобнее брать более мелкие короткие интервалы, а там где реже - более крупный.
Замечание №2. Появление “граничных” значений 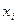 нежелательно, это ведет к смещению эмпирического распределения от его истинного положения на числовой оси влево, либо вправо, выбирая границы, регулирования длину интервала, следует этого избегать.
нежелательно, это ведет к смещению эмпирического распределения от его истинного положения на числовой оси влево, либо вправо, выбирая границы, регулирования длину интервала, следует этого избегать.
Замечание №3 Если для некоторых значений получены “нулевые”, либо малые значения частот 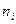 , то необходимо перегруппировать данные, укрупняя интервалы (увеличивая шаг
, то необходимо перегруппировать данные, укрупняя интервалы (увеличивая шаг 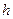 ).
).
Этап II. Графическое изображения ряда и эмпирической функции распределения.
Графически интервальный вариационный ряд изображается либо в виде гистограммы частот – ступенчатой фигуры, состоящей из прямоугольников, основанием которых служат интервалы группировки, а высоты равны отношению частоты к длине интервала 
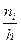 , либо в виде гистограммы относительных частот, когда высоты прямоугольников равны отношению относительной частоты к длине интервала группировки
, либо в виде гистограммы относительных частот, когда высоты прямоугольников равны отношению относительной частоты к длине интервала группировки 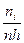 .
.
Дискретный вариационный ряд графически изображается в виде полигона частот или относительных частот.
Полигон частот – это ломаная линия, отрезки которой соединяют точки с координатами (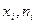 ).
).
Полигон относительных частот – это ломанная линия, отрезки которой соединяются точками с координатами (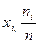 ).
).
Эмпирическая функция распределения графически изображается в виде линии, изменяющейся скачкообразно. На оси абсцисс откладывается значения интервалов, на оси ординат соответствующие им вероятности (значения функции), вычисляемые по формуле 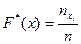 , где
, где 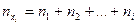 .
.
Скачки наблюдаются при переходе от одного интервала к другому.
Графическое изображение вариационных рядов и эмпирической функции распределения лучше уяснить на конкретном примере в разделе “Образец выполнения задания”.
Этап III. Вычисление числовых характеристик.
Вычисление числовых характеристик осуществляются по следующим формулам:
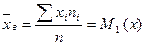 .
.
2. Дисперсия вычисляется либо по определению
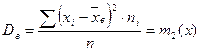
либо по формуле 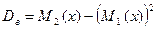 , где
, где 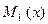 и
и 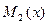 - начальные эмпирические моменты первого и второго порядков.
- начальные эмпирические моменты первого и второго порядков.
3. Среднее квадратическое отклонение
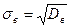 .
.
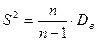 .
.
5. Исправленное среднее квадратическое отклонение
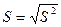 .
.
6. Коэффициент асимметрии
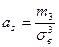
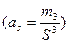 ,
,
где 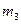 - центральный эмпирический момент третьего порядка, он вычисляется либо по определению
- центральный эмпирический момент третьего порядка, он вычисляется либо по определению
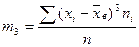 ,
,
либо по формуле
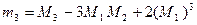 ,
,
где 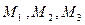 - начальные эмпирические моменты первого, второго и третьего порядков.
- начальные эмпирические моменты первого, второго и третьего порядков.
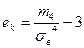 ,
,
где 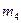 - центральный эмпирический момент четвертого порядка. Он вычисляется либо по определению
- центральный эмпирический момент четвертого порядка. Он вычисляется либо по определению
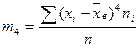
либо по формуле 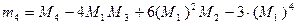 ,
,
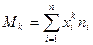 ,
, 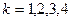
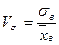 ,
, 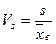
(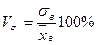 ,
, 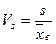 )
)
Замечание 1: Так как все числовые характеристики выражаются через 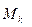 , то удобнее вначале вычислить числовые значения
, то удобнее вначале вычислить числовые значения 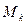 , а затем значения числовых характеристик.
, а затем значения числовых характеристик.
Замечание 2: Для упрощения расчетов, если они выполняются “вручную” удобнее перейти от данных значений вариант 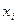 к условиям
к условиям 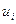 по формуле
по формуле
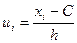 ,
,
где h – длина интервала группировки,
С – ложный нуль.
Чаще всего в качестве ложного нуля принимается либо варианта, находящаяся в середине вариационного ряда, либо мода 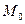 (варианта
(варианта 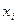 , имеющая наибольшую частоту), либо любое другое число, упрощающее расчеты.
, имеющая наибольшую частоту), либо любое другое число, упрощающее расчеты.
Если за 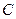 принять какое - либо значение
принять какое - либо значение 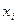 , то соответствующая ему условная варианта
, то соответствующая ему условная варианта 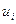 будет равна нулю, а слева и справа от нуля будут располагаться соответственно значения
будет равна нулю, а слева и справа от нуля будут располагаться соответственно значения 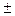 1,
1, 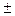 2,
2, 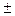 3,
3, 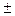 4 и т.д.
4 и т.д.
Если, например, 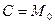 , то вариационный ряд в условных вариантах примет вид
, то вариационный ряд в условных вариантах примет вид
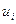 | … | -2 | -1 | … | |||
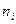 | … | 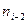 | 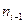 | 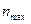 | 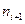 |  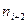 | … |
Числовые характеристики в условных вариантах 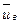 ,
, 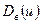 ,
, 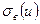 , вычисляют с той лишь разницей, что вместо
, вычисляют с той лишь разницей, что вместо 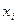 используется
используется 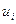 .
.
Однако после вычисления числовых характеристик в условных вариантах необходимо перейти к первоначальным значениям вариант. Это осуществляется по формулам:
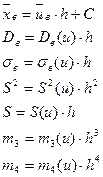
Промежуточные расчеты при вычислении числовых характеристик удобнее оформлять в виде таблицы.
Этап IV. Определение границ истинных значений числовых характеристик изучаемой величины с заданной надежностью.
Числовые характеристики, вычисленные по случайной выборке из генеральной совокупности, лишь приближенно характеризуют истинные значения аналогичных характеристик изучаемой генеральной совокупности. Поэтому возникает вопрос о надежности, с которой можно принять вычисленные значения и о границах допустимых значений. Частично эти вопросы решаются путем нахождения доверительных (надежностных) интервалов для основных числовых характеристик.
Надежностный интервал для генеральной средней имеет вид:
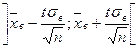 или
или 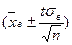 ,
,
где
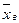 - среднее выборочное
- среднее выборочное
n – объем выборки
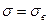 , если большая выборка (
, если большая выборка (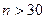 ),
),
t – значение аргумента функции Лапласа, при котором она равна 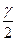 ,
,
t – находится по таблицам значений функции Лапласа из условия
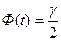
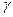 - вероятность суждений, называемая надежностью. Она выбирается самим исследователем. Значения
- вероятность суждений, называемая надежностью. Она выбирается самим исследователем. Значения 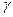 =0.95, как правило, считается достаточным для большинства исследований. Надежностный интервал с вероятностью содержит в себе генеральную среднюю.
=0.95, как правило, считается достаточным для большинства исследований. Надежностный интервал с вероятностью содержит в себе генеральную среднюю.
Замечание. Если выборка мала (n<30), то надежностный интервал для генеральной средней имеет вид:
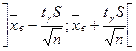
где S – исправленное выборочное среднеквадратическое отклонение,
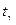 - число, взятое из таблицы значений
- число, взятое из таблицы значений 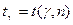 по объему выборки n и надежности
по объему выборки n и надежности 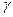 .
.
При больших n результаты нахождения надежноcтного интервала двумя указанными способами практически неразличимы.
Надежностный интервал для среднеквадратического отклонения имеет вид
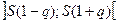 ,
,
т.е. определяется выражением 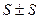 ∙ q или, если левая часть отрицательна, то ее отбрасывают и интервал примет вид
∙ q или, если левая часть отрицательна, то ее отбрасывают и интервал примет вид
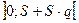 ,
,
где S - исправленное выборочное среднее квадратическое отклонение,
q – табличное значение критических точек 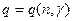 , оно зависит от объема выборки n и заданной надежности
, оно зависит от объема выборки n и заданной надежности 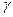 .
.
Этап V. Содержательная интерпретация результатов первичной обработки данных по условию задачи.
Итогом первичной обработки данных служит содержательная интерпретация результатов произведенных вычислений.
Арифметическое среднее, вычисленное по выборочным данным, 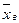 представляет собой обобщенную характеристику всей совокупности значений в целом. Значение
представляет собой обобщенную характеристику всей совокупности значений в целом. Значение 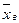 - являясь как бы точкой сгущения значений, характеризует центральное положение возможных значений случайной величины.
- являясь как бы точкой сгущения значений, характеризует центральное положение возможных значений случайной величины.
Доверительный интервал 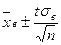 указывает на то, что с вероятностью
указывает на то, что с вероятностью 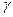 , генеральная средняя
, генеральная средняя 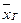 изучаемой случайной величины заключена в найденном интервале, или, что данный интервал с надежностью
изучаемой случайной величины заключена в найденном интервале, или, что данный интервал с надежностью 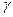 содержит в себе истинное среднее значение генеральной совокупности
содержит в себе истинное среднее значение генеральной совокупности 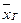 .
.
Среднее квадратическое отклонение 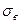 служит показателем, который дает представление о наиболее вероятной средней ошибке отдельного, единичного наблюдения, взятого из данной совокупности.
служит показателем, который дает представление о наиболее вероятной средней ошибке отдельного, единичного наблюдения, взятого из данной совокупности.
Основные значения, ядро вариационного ряда содержится в интервале
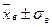 , или
, или 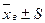 .
.
Отклонение от 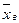 , превосходящее по модулю
, превосходящее по модулю 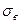
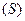 возможны, но вероятность их уменьшается по мере удаления от
возможны, но вероятность их уменьшается по мере удаления от 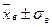 ,
, 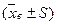 .
.
Надежностный интервал 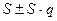 с вероятностью
с вероятностью 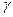 содержит в себе значение генерального среднего квадратического отклонения.
содержит в себе значение генерального среднего квадратического отклонения.
Коэффициент асимметрии 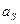 - указывает на нарушение симметрии, наличие скоса.
- указывает на нарушение симметрии, наличие скоса.
Если 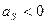 , то скос наблюдается справа, если
, то скос наблюдается справа, если 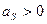 , то слева, если
, то слева, если 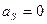 , то распределение симметричное.
, то распределение симметричное.
Коэффициент эксцесса 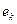 - указывает на характер вершины распределения.
- указывает на характер вершины распределения.
Если 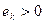 , то распределение островершинное, это говорит о том, что значения признака не значительно разбросаны вокруг среднего значения. Если
, то распределение островершинное, это говорит о том, что значения признака не значительно разбросаны вокруг среднего значения. Если 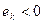 , то распределение пологое, это говорит о том, что значения признака значительно разбросаны вокруг среднего значения. Если
, то распределение пологое, это говорит о том, что значения признака значительно разбросаны вокруг среднего значения. Если 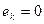 , то распределение совпадает со стандартным нормальным.
, то распределение совпадает со стандартным нормальным.
Коэффициент вариации V – стандартное отклонение, выраженное в процентах к средней арифметической данной совокупности. Он является относительным показателем изменчивости. Если V <10%, то изменчивость считают незначительной, если 10%< V <20% то изменчивость считают средней, если V >20%, то изменчивость значительная.
Использование коэффициента вариации V как показателя колеблемости (вариации) имеет смысл только при положительных значениях вариант и совершенно не применимо, если варианты принимают как положительные так и отрицательные значения.
Рассмотренные числовые характеристики необходимо сопоставлять с вариационным рядом, его графическим изображением и интерпретировать с учетом единиц измерения и содержания, указанных в условиях задачи.
 2015-01-30
2015-01-30 2596
2596