Погрешности измерений

1.3.1. Основные понятия и виды погрешностей

Процедура измерений состоит из следующих основных этапов: принятие модели объекта измерения, выбор метода измерений, выбор средств измерений, проведение эксперимента для получения численного значения результата измерения. Различного рода недостатки, присущие этим этапам, приводят к тому, что результат измерения отличается от истинного значения измеряемой величины.

Причины возникновения погрешности могут быть различными. Измерительные преобразования осуществляются с использованием различных физических явлений, на основании которых можно установить соотношение между измеряемой величиной объекта исследования и выходным сигналом средства измерений, по которому оценивается результат измерения. Точно установить это соотношение никогда не удается вследствие недостаточной изученности объекта исследования и неадекватности его принимаемой модели, невозможности точного учета влияния внешних факторов, недостаточной разработанности теории физических явлений, положенных в основу измерения, использования простых, но приближенных аналитических зависимостей вместо более точных, но сложных и т.д. В результате принимаемая зависимость между измеряемой величиной и выходным сигналом средства измерений всегда отличается от реальной, что приводит к погрешности, которую называют методической погрешностью измерения.

В погрешность измерения входит погрешность средств измерений, используемых в эксперименте. Допускаемые значения основной погрешности средств измерений указывают в нормативно - технической документации на эти средства и могут быть указаны на самих средствах. В условиях эксперимента у применяемых средств измерений могут возникнуть дополнительные погрешности из-за влияния внешних факторов (например, температура окружающей среды, внешнее магнитное поле), неправильной установки прибора (например, вертикальная или наклонная установка прибора, который должен устанавливаться горизонтально).

Следует также иметь в виду, что включение средства измерений в цепь, где производится измерение, может изменить режим цепи за счет взаимодействия средства измерений с цепью (с объектом измерения). Указанные погрешности, обусловленные несовершенством свойств используемых средств измерений, образуют инструментальную составляющую погрешности измерений.

В процессе измерения часто принимает участие экспериментатор. Он может внести субъективную погрешность, которая является следствием индивидуальных свойств человека, обусловленных физиологическими особенностями его организма, скоростью реакции или укоренившимися неправильными навыками. Например, если нескольким экспериментаторам поручить установить одно и то же значение тока в цепи по аналоговому амперметру, то при всей тщательности установки значения тока будут отличаться друг от друга.

При проведении эксперимента может появиться необходимость в обработке промежуточных результатов измерений. Для этих целей удобно использовать средства вычислительной техники (микрокалькуляторы, микро- или мини-ЭВМ). Они могут внести свою составляющую погрешности, обусловленную неточностью выполнения вычислительных операций.

Таким образом, погрешность измерения образуется из методической погрешности, инструментальной погрешности, погрешности вычислений и погрешности, вносимой оператором.

В основу приведенной классификации погрешностей положены причины возникновения погрешностей.

В зависимости от режима работы (статического или динамического) используемого средства измерений различают погрешности в статическом режиме (статические погрешности) и погрешности в динамическом режиме. В статическом режиме измеряемая величина и выходной сигнал (например, отклонение указателя), по которому оценивают результат измерения, являются неизменными во времени. В динамическом режиме выходной сигнал изменяется во времени. Типичным примером динамического режима работы средства измерений является измерение изменяющейся во времени величины. При измерении постоянной величины динамический режим возникает при подключении средства измерений к исследуемому объекту и продолжается до тех пор, пока выходной сигнал не достигает постоянного установившегося значения. Особенностью динамического режима является то, что, помимо перечисленных выше погрешностей, характерных для статического режима, здесь возникает погрешность, обусловленная инерционными свойствами средства измерений. Инерция (тепловая, механическая, электрическая) средства измерений приводит к тому, что выходной сигнал не сможет успевать правильно реагировать на быстрые изменения входной измеряемой величины, искажая таким образом представление о характере этих изменений. Погрешность, обусловленную инерционными свойствами, называют динамической погрешностью и определяют ее как разность между погрешностью в динамическом режиме и статической погрешностью, соответствующей значению измеряемой величины в данный момент времени.

В зависимости от способа выражения погрешности измерения различают абсолютную и относительную погрешности. Абсолютную погрешность Dх=х-х_о выражают в единицах измеряемой величины. Более наглядной характеристикой точности при сравнении различных результатов измерения является относительная погрешность: d =Dх/х_о » Dх/х. Знак относительной погрешности определяется знаком Dх. Относительная погрешность может быть выражена в процентах. Здесь х- показание средства измерения, х₀- истинное значение измеряемой величины.

В зависимости от характера изменения различают:

1) систематическую погрешность измерения - составляющую погрешности измерения, остающуюся постоянной или закономерно изменяющую при повторных измерениях одной и той же величины;

2) случайную погрешность измерения - составляющую погрешности измерения, изменяющуюся случайным образом при повторных измерениях одной и той же величины.

Систематические погрешности. Наличие систематических погрешностей может быть обнаружено путем анализа условий проведения эксперимента или повторными измерениями одного и того же значения измеряемой величины разными методами или приборами. Примером постоянной систематической погрешности может быть погрешность, обусловленная несоответствием истинного значения меры, например измерительной катушки сопротивления при косвенном измерении тока, с помощью которой производится измерение, ее номинальному значению.

Примером переменной систематической погрешности может быть погрешность от закономерного изменения напряжения вспомогательного источника питания (разряд аккумулятора),если результат измерения зависит от значения этого напряжения. Систематические погрешности могут быть в значительной степени исключены или уменьшены устранением источников погрешностей или введением поправок, устанавливаемых на основании предварительного изучения погрешностей мер и приборов, применяемых при измерении, использованием поправочных формул и кривых, выражающих зависимость показаний приборов от внешних условий (например, температуры) и т.д. Систематические погрешности могут быть также исключены путем нескольких проведенных определенным образом измерений. Применение того или иного способа зависит от требуемой точности, условий проведения эксперимента, наличия поправочных формул и других причин.

Следует иметь в виду, что полностью исключить систематические погрешности невозможно, так как методы и средства, с помощью которых обнаруживаются и оцениваются систематические погрешности, сами имеют свои погрешности. Поэтому всегда остается неисключенный остаток систематической погрешности.

Случайные погрешности. Эти погрешности, как правило, вызываются сложной совокупностью изменяющихся факторов, обычно неизвестных экспериментатору и трудно поддающихся анализу. Иногда причины, вызывающие случайные погрешности, могут быть известны (например, наводки от внешних электромагнитных полей), но если эти причины сами по себе имеют случайный, хаотический характер, то и погрешности, вызванные ими, будут тоже случайными.

Если причины появления случайных погрешностей известны, то для уменьшения этих погрешностей уменьшают влияние причин на результат измерения (например, экранируют цепи). При невозможности устранения этих причин или когда они неизвестны, влияние случайных погрешностей на результат измерения можно уменьшить путем проведения многократных измерений одного и того же значения измеряемой величины с дальнейшей статистической обработкой полученных результатов методами теории вероятностей.

Иногда к систематическим погрешностям применяют такой же подход, как к случайным. Так, например, не исключенный остаток систематической погрешности рассматривают, как случайную величину, которая может иметь любое значение в пределах погрешности средств измерений, с помощью которых выявлялась систематическая погрешность. Аналогично следует поступать в тех случаях, когда систематическая погрешность по тем или иным причинам не может быть исключена в процессе эксперимента. Например, систематическая погрешность от влияния температуры окружающей среды на используемое средство измерений может быть хорошо изучена и составлены таблицы поправок для исключения этой погрешности, но по условиям эксперимента температура не изменяется. В этом случае поправку ввести невозможно, но можно утверждать, что систематическая погрешность имеет некоторое значение в пределах, соответствующих возможному диапазону изменения температуры в процессе эксперимента, т.е. рассматривать эту погрешность как случайную величину.

Кроме перечисленных погрешностей измерения, встречается так называемая грубая погрешность измерения, существенно превышающая ожидаемую погрешность при данных условиях. Результат измерения, содержащий грубую погрешность, иногда называют промахом. Он возникает при внезапных кратковременных изменениях условий эксперимента, например при кратковременном отключении источника питания механическом ударе, при неправильном отсчете экспериментатором показаний средств измерений и т.п. Грубые погрешности по своей природе тоже случайны и не могут быть предсказаны заранее. Промахи можно выявить путем обработки методами теории вероятностей результатов повторных измерений одного и того же значения измеряемой величины. После выявления они должны быть исключены.

Результат измерения всегда содержит как систематическую, так и случайную погрешности. Поэтому погрешность результата измерения Dх в общем случае нужно рассматривать как случайную величину, тогда систематическая погрешность Dх_с есть математическое ожидание этой величины, а случайная погрешность Dх - центрированная случайная величина. При этом Dх=Dх_с+ Dх.

1.3.2.Вероятностный подход к описанию

погрешностей

Полным описанием случайной величины, а следовательно и погрешности, является ее закон распределения, которым определяется характер появления различных результатов отдельных измерений. В практике измерений встречаются различные законы распределения, некоторые из которых рассмотрены ниже.

Нормальный закон распределения (закон Гаусса). Этот закон является одним из наиболее распространенных законов распределения погрешностей. Объясняется это тем, что во многих случаях погрешность измерения образуется под действием большой совокупности различных, независимых друг от друга причин. На основании центральной предельной теоремы теории вероятностей результатом действия этих причин будет погрешность, распределенная по нормальному закону при условии, что ни одна из этих причин не является существенно преобладающей.

Нормальный закон распределения погрешностей описывается формулой

w (Dx) = 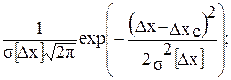(1.1)

где w (Dx) - плотность вероятности погрешности Dx; s[Dx] - среднее квадратическое отклонение погрешности; Dх_с - систематическая составляющая погрешности.

Вид нормального закона, описываемого выражением (1.1) представлен на рис. 1.4 для двух значений s[Dх]. Так как Dx=Dx-Dх_с, то закон распределения случайной составляющей огрешности w (Dx) имеет тот же вид (рис.1.5) и описывается выражением, аналогичным, (1-2), т.е

w (Dx)= 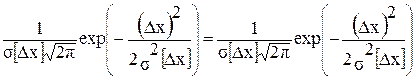; (1.2)

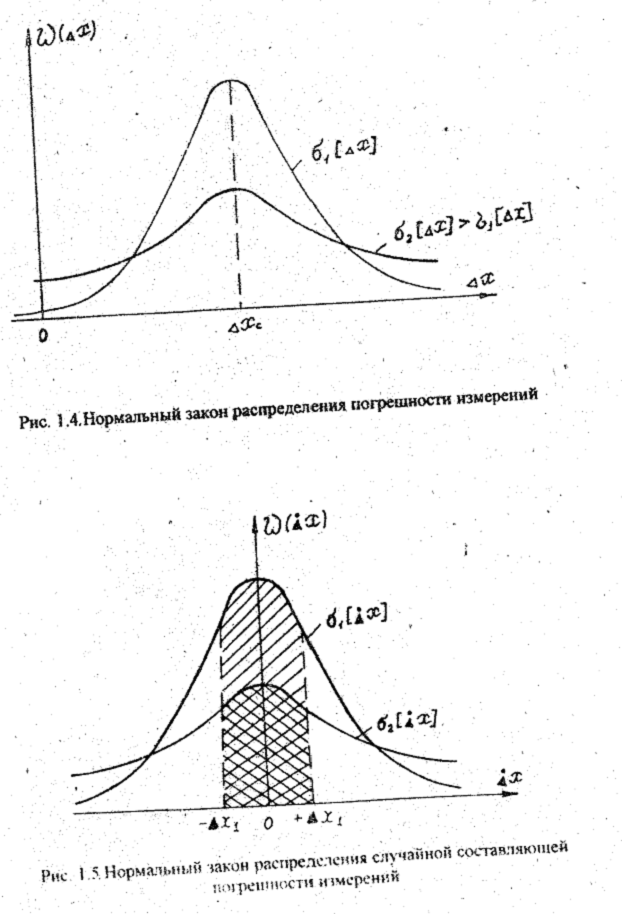
где s[Dx] - среднее квадратичное отклонение случайной составляющей погрешности; s[Dx]= s[Dx].

Таким образом, закон распределения погрешности Dх отличается от закона распределения случайной составляющей погрешности Dх только сдвигом по оси абсцисс на величину систематической составляющей погрешности Dх _с.

Из теории вероятностей известно, что площадь под кривой плотности вероятности характеризует вероятность появления погрешности. Из рис.1.5 видно, что вероятность Р появления погрешности в диапазоне ± Dх₁ при s₁[Dx] больше, чем при s₂[Dx] (площади, характеризующие эти вероятности, заштрихованы). Полная площадь под кривой распределения всегда равна 1, т.е. полной вероятности. Учитывая это, можно утверждать, что погрешности, абсолютные значения которых превышают [Dx₁], появляются с вероятностью, равной 1 - Р, которая при s₁[Dx] меньше, чем при s₂[Dx]. Следовательно, чем меньше s[Dx], тем реже встречаются большие погрешности, тем точнее выполнены измерения. Таким образом, среднее квадратичное отклонение s[Dx] можно использовать для характеристики точности измерений:

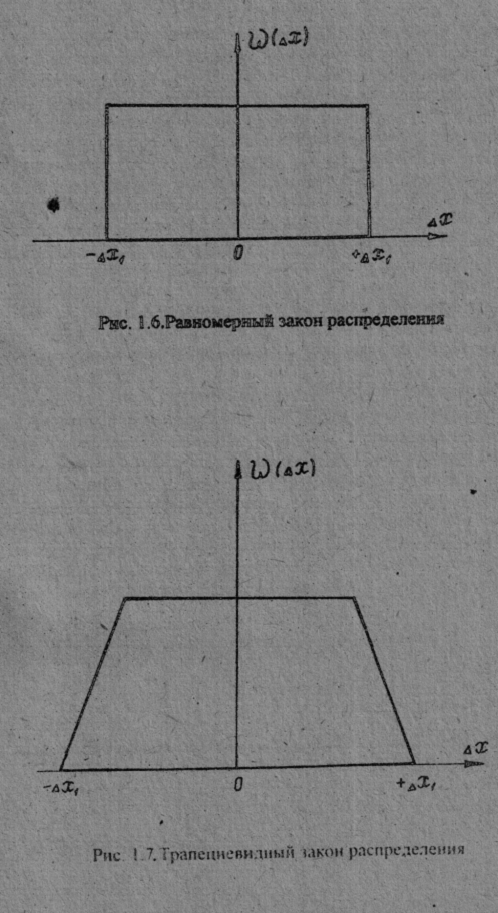
Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешности w(Dx) постоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис.1.6. Аналитически он может быть записан так:

w(Dx)= 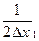при - Dх₁ £ Dх £ +Dх₁ (1.3)

w (Dx)=0 при Dх < - Dх₁ и Dх > - Dх₁ (1.4)

С таким законом распределения хорошо согласуется погрешность от трения в опорах электромеханических приборов, не исключенные остатки систематической погрешностей, погрешность дискретности в цифровых приборах и др.

Трапециевидный закон распределения. Это распределение графически изображено на рис.1.7. Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерным законом различна. Например, при последовательным соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале ±Dx₁, а другой - равномерно распределенную в интервале ±Dx₂, суммарная погрешность преобразования будет описываться трапециевидным законом распределения.

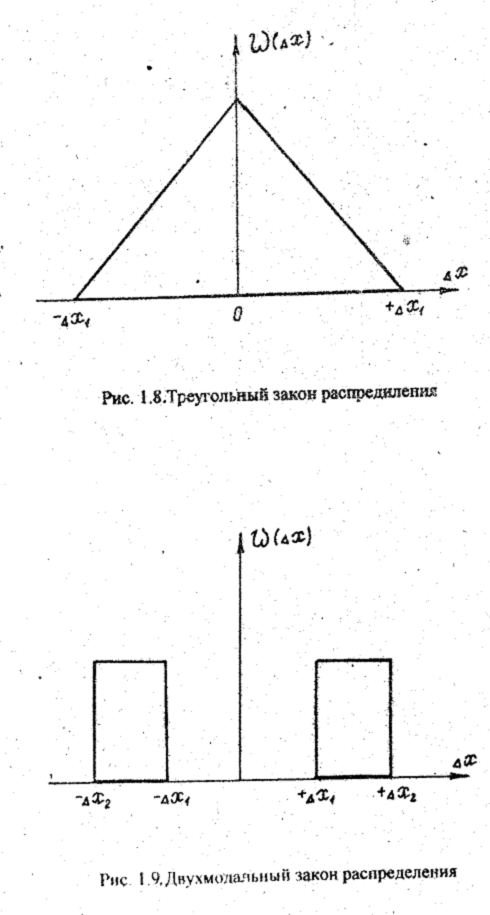
Треугольный закон распределения (закон Симпсона). Это распределение (см.рис.1.8) является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения.

Двухмодальные законы распределения. В практике измерений встречаются двухмодальные законы распределения, т.е. законы распределения, имеющие два максимума плотности вероятности. В качестве примера на рис.1.9 изображен двухмодальный закон распределения, который может быть в приборах, имеющих погрешность от люфта кинематических механизмов или от гистерезиса при перемагничивании деталей прибора.

Если законы распределения погрешностей неизвестны, то они могут быть установлены на основании статистической обработки опытных данных рис.1.10. Однако экспериментальное определение законов распределения весьма трудоемко, поэтому к нему прибегают лишь при весьма ответственных измерениях.

Иногда закон распределения погрешности принимают, исходя из физического представления о причинах появления погрешностей и анализа составляющих погрешностей измерения. Так, например, если погрешность измерения образуется из пяти и более составляющих, среди которых нет существенно преобладающих, то закон распределения результирующей погрешности обычно принимают нормальным. В противном случае, анализируя составляющие погрешности, принимают для них вид законов распределения и методами теории вероятностей находят закон распределения для результирующей (суммарной) погрешности измерения.

Из сказанного следует, что точный вид закона распределения погрешностей обычно неизвестен. Реальные законы распределения даже в простейших случаях отличаются от теоретических стандартных законов распределения, рассмотренных выше, где они называются стандартными аппроксимациями функций плотности вероятности. Поэтому характеристики погрешности не удается найти точно. Однако практика показывает, что погрешность 10-20% при определении самой погрешности зачастую вполне удовлетворительна.

1.3.3. Вероятностные оценки погрешностей

В результате измерения получают значение измеряемой величины в виде числа в принятых единицах величины. Погрешность измерения тоже удобно выражать в виде числа. Однако погрешность измерения является случайной величиной, исчерпывающим описанием которой может быть только закон распределения.

Из теории вероятностей известно, что закон распределения можно охарактеризовать числовыми характеристиками (неслучайными числами), которые и используются для количественной оценки погрешности.

Основными числовыми характеристиками законов распределения являются математическое ожидание и дисперсия, которые определяются выражениями:

M[Dх] 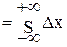w (Dx) d (Dx); (1.5)

D[Dх] 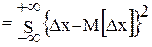w(Dx)d(Dx)=D[Dх] 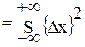w(Dx)d(Dx); (1.6)

где М - символ математического ожидания; D - символ дисперсии.

Математическое ожидание погрешности измерений есть неслучайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях. Математическое ожидание харак систематическую составляющую погрешности измерения, т.е. М [Dx] = Dx_с. Как числовая характеристика погрешности М[Dх] показывает на смещенность результатов измерения относительно истинного значения измеряемой величины.

Дисперсия погрешности D[Dх] характеризует степень рассеивания (разброса) отдельных значений погрешности относительно математического ожидания. Так как рассеивание происходит за счет случайной составляющей погрешности, то D[Dx] = D[Dx]. Чем меньше дисперсия, тем меньше разброс, тем точнее выполнены измерения. Следовательно, дисперсия может служить характеристикой точности проведенных измерений. Однако дисперсия выражается в единицах погрешности в квадрате. Поэтому в качестве числовой характеристики точности измерений используют среднее квадратическое отклонение s[Dх] = 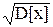с положительным знаком выражаемое в единицах погрешности.

Обычно при проведении измерений стремятся получить результат измерений с погрешностью, не превышающей допускаемое значение. Знание только среднего квадратического отклонения не позволяет найти максимальную погрешность, которая может встретиться при измерениях, что свидетельствует об ограниченных возможностях такой числовой характеристики погрешности, как s[Dх]. Более того, при условиях измерений, когда законы распределения погрешностей могут отличаться друг от друга, погрешность с меньшей дисперсией может принимать большие значения.

Максимальные значения погрешности зависят не только от s[Dх], но и от вида закона распределения. Когда распределение погрешности теоретически неограниченно, например, при нормальном законе распределения, погрешность может быть любой по значению. В этом случае можно лишь говорить об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным интервалом, характеризующую его вероятность - доверительной вероятностью, а границы этого интервала - доверительными значениями погрешности.

В практике измерений применяют различные значения доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений. Так, например, при нормальном законе распределения случайных погрешностей со средним квадратическим отклонением s[Dх] часто пользуются доверительным интервалом от +3s[Dх] до -3s[Dх], для которого доверительная вероятность равна 0,9973. Такая доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет больше 3s[Dх]. Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей, чем 3s[Dх], маловероятное событие, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению 3s[Dх] (правило "трех сигм").

В соответствии с ГОСТ 8.011-72 доверительный интервал является одной из основных характеристик точности измерений. Одну из форм представления результата измерения этот стандарт устанавливает в следующем виде: х; Dх от Dх_н до Dх_в; P, где х - результат измерения в единицах измеряемой величины; Dх, Dх_н, Dх_в - соответственно погрешность измерения с нижней и верхней ее границами в тех же единицах; Р - вероятность, с которой погрешность измерения находится в этих границах.

ГОСТ 8.011-72 допускает и другие формы представления результата измерения, отличающиеся от приведенной формы тем, что в них указывают раздельно характеристики систематической и случайной составляющих погрешности измерения. При этом для систематической погрешности указывают ее вероятностные характеристики. Ранее уже отмечалось, что иногда систематическую погрешность приходится оценивать с вероятностных позиций. В этом случае основными характеристиками систематической погрешности являются М [Dx_с], s[Dx_с] и ее доверительный интервал. Выделение систематической и случайной составляющих погрешности целесообразно, если результат измерения будет использован при дальнейшей обработке данных, например при определении результата косвенных измерений и оценке его точности, при суммировании погрешностей и т.п.

Любая из форм представления результата измерения, предусмотренная ГОСТ8.011-72, должна содержать необходимые данные, на основании которых может быть определен доверительный интервал для погрешности результата измерения. В общем случае доверительный интервал может быть установлен, если известен вид закона распределения погрешности и основные числовые характеристики этого закона.

1.3.4. Основы метрологического обеспечения

Развитие науки и техники неразрывно связано с возрастанием роли измерений. Автоматизация управления производственными процессами, техническими объектами и исследованиями ставит перед измерительной техникой новые и ответственные задачи, связанные с усложнением измерительных процедур, повышением точности, быстродействия и т.п. Многообразие видов измерений и средств измерений неуклонно возрастает, причем это качественное и количественное развитие измерений должно идти в рамках обеспечения единства измерений, под которым понимается выражение результата измерения в указанных единицах с указанием значений характеристик погрешностей.

Возникло новое понятие - метрологическое обеспечение, под которым понимают установление и применение научных и организационных основ, технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерений.

Научной основой метрологического обеспечения является метрология - наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности измерений.

Организационной основной метрологического обеспечения является метрологическая служба России, состоящая из государственной и ведомственной служб. Под метрологической службой подразумевается сеть учреждений и организаций, возглавляемых Госстандартом России, деятельность которых направлена на метрологическое обеспечение.

Техническую основу метрологического обеспечения составляют: система государственных эталонов единиц физических величин; система передачи размеров единиц физических величин от эталонов всем средствам измерений с помощью образцовых средств измерений и средств поверки; система государственных испытаний средств измерений, обеспечивающая единообразие средств измерений при разработке и выпуске их в обращение; система обязательной поверки или метрологической аттестации средств измерений; система стандартных образцов состава и свойств веществ и материалов; система стандартных справочных данных о физических константах и свойствах веществ и материалов.

Правовую основу метрологического обеспечения составляет Государственная система обеспечения единства измерений (ГСИ), представляющая собой комплекс нормативно - технических документов, устанавливающих единую номенклатуру стандартных взаимосвязанных правил и положений, требований и норм, относящихся к организации и методике оценивания и обеспечения точности измерений.

Основными объектами стандартизации ГСИ являются: единицы физических величин; государственные эталоны и общесоюзные поверочные схемы; методы и средства поверки средств измерений; номенклатура нормируемых метрологических характеристик средств измерений; нормы точности измерений; способы выражения и формы представления результатов измерения и показателей точности измерений; методики выполнения измерений; организация и порядок проведения государственных испытаний, поверки, метрологической аттестации средств измерений; термины и определения в области метрологии и т. д.

Для обеспечения единства измерений ГСИ требует выполнения следующих положений. Результаты измерений должны выражаться в единицах физических величин, допущенных к применению в России по ГОСТу 8.417-81 (СТ СЭВ 1052-78) “ГСИ. Единицы физических величин”. В соответствии с этим стандартом основными единицами являются: метр (м) - единица длины; килограмм (кг) - единица массы; секунда (с) - единица времени; ампер (А) - единица силы тока; кельвин (К) - единица термодинамической температуры; моль (моль) - единица количества вещества; кандела (кд) - единица силы света.

К дополнительным единицам относят радиан (рад) - единица плоского угла и стерадиан (ср) - единица телесного угла. Кроме основных и дополнительных, система единиц предусматривает производные единицы, образуемые из основных и дополнительных при помощи определяющих уравнений. Угловые единицы не могут быть введены в число основных, так как это вызвало бы затруднение в трактовке размерностей величин, связанных с вращением (дуги окружности, площади круга, работа пары сил и т. п.). Вместе с тем они не являются и производными единицами, так как не зависят от выбора основных единиц. Допускаются к применению также внесистемные единицы.

Средства измерений, предназначенные к серийному выпуску, подлежат государственным испытаниям. Основными целями государственных (приемочных и контрольных) испытаний является установление соответствия выпускаемых в стране серийно и закупаемых за границей средств измерений требованиям стандартов и техническим заданиям.

Средства измерений, находящиеся в пользовании, должны периодически подвергаться государственной поверке, ревизии, экспертизе. Поверка средств измерений производится для установления пригодности их к применению. Ревизия средств измерений производится для установления соответствия средств и методик измерений необходимому уровню метрологического обеспечения производства. Экспертиза производится в тех случаях, когда возникают вопросы о соответствии средств измерений и методик их применения техническим условиям.

Метрологические характеристики средств измерений, подлежащие нормированию, должны соответствовать государственным стандартам, которые устанавливают номенклатуру метрологических характеристик, средств измерений, а также способы их представления в нормативно - технической документации.

Форма представления результатов измерений должна соответствовать стандартам. В номенклатуру устанавливаемых стандартом показателей входят функции распределения вероятности систематической и случайной погрешностей результатов измерений, числовые характеристики систематической и случайной погрешностей, а также интервалы, в которых погрешности результатов измерений находятся с заданной вероятностью.

Измерения, нормы точности которых регламентированы стандартами или нормативно - техническими документами, должны выполняться по стандартным или аттестованным методикам выполнения измерений.

1.4. Эталоны единиц физических величин

Государственная система обеспечения единства измерений устанавливает требования к эталонам единиц физических величин и к системе передачи размера единицы каждой величины к рабочим средствам измерений.

Эталоны единиц физических величин - средства измерений (или комплексы средств измерений), обеспечивающие воспроизведение и (или) хранение единиц с целью передачи их размеров рабочим средствам измерений. Передача размеров осуществляется с помощью поверочных схем.

В настоящее время в стране действует примерно 130 эталонов единиц физических величин. Эталоны единиц классифицируют по ряду признаков. Соответственно делению физических величин различают эталоны основных и производных единиц, а по точности воспроизведения единиц и подчиненности - первичные (исходные) и вторичные.

Первичные эталоны воспроизводят и (или) хранят единицы и передают их размеры с наивысшей точностью, достижимой в данной области измерений. Разновидностью первичных эталонов являются специальные эталоны, предназначенные для воспроизведения единиц в установленных особых условиях (сверхвысокие частоты, малые и большие энергии, давления, температуры и т. п.). Первичные и специальные эталоны, официально утвержденные в качестве исходных для страны, называют государственными, на каждый из них утверждают государственный стандарт.

К вторичным эталонам относят эталоны - копии, эталоны сравнения и рабочие эталоны. Эталоны - копии предназначены для передачи размера единицы рабочим эталонам, которые служат для поверки образцовых и наиболее точных рабочих средств измерений. Эталоны сравнения предназначены для взаимного сличения эталонов, которые не могут быть непосредственно сличены друг с другом.

По своему составу эталоны могут быть одиночные и групповые. Одиночный эталон представляет собой одну меру (прибор или установку), а групповой эталон состоит из однотипных мер (измерительных устройств), воспроизводящих размер единицы в виде среднего арифметического результатов воспроизведения каждым из элементов этой совокупности.

Кроме национальных эталонов, имеются международные эталоны, принадлежащие группе стран и предназначенные для поддержания единства измерений в международном масштабе путем периодического сличения национальных эталонов с международным и между собой.

Государственный первичный эталон единицы массы - килограмма состоит из национального прототипа килограмма (гири из платино-иридевого сплава) и эталонных весов, предназначенных для передачи размера единицы массы вторичным эталонам. Среднее квадратическое отклонение относительной погрешности воспроизведения эталоном единицы массы равно 7*10⁹.

В настоящее время ведутся работы по созданию "естественного" эталона единицы массы, например, используя счет числа молекул.

Государственный первичный эталон единиц длины - комплекс средств, воспроизводящих метр в виде 1650763,73 длин волн излучения в вакууме, соответствующего переходу между определенными уровнями атома криптона-86. Эталон обеспечивает воспроизведения метра с относительным средним квадратическим отклонением результата измерений, не превышающим 5*10⁹.

Государственный первичный эталон единицы времени - комплекс средств, воспроизводящих секунду в виде 192 631 770 периодов колебаний электромагнитного излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия - 133. Этот эталон является также эталоном единицы частоты - герца. Он обеспечивает воспроизведение единиц с относительным средним квадратическим отклонением результата измерений, не превышающим 1*10^-13, при неисключенной относительной систематической погрешности, не превышающей 1*10 ^-12 .

Появление высокостабильных лазеров позволило осуществить согласованное определение метра и секунды на основе одной линии излучения. В связи с этим в 1983г. XVII Генеральной конференцией по мерам и весам принято решение о новом определении метра, в соответствии с которым, метр определен как длина пути, проходимого светом за 1/299 792 548 долю секунды. В настоящее время ведутся работы по созданию единого эталона единиц времени, частоты и длины. При этом используется фундаментальная зависимость l =ct, где l - путь, проходимый излучением; с =299 792 548 м/с - скорость света (излучения); t - время.

Государственный первичный эталон единицы силы постоянного тока – ампера - это комплекс средств, в состав которых входят токовые весы. B токовых весах, представляющих собой рычажные равноплечие весы, с одной стороны на коромысло действует сила взаимодействия двух солиноидов, обтекаемых постоянным током, а с другой стороны - гиря известной массы. При равновесии весов сила тока определяется через массу гири, ускорение свободного падения в месте расположения весов и постоянную электродинамической системы (двух соленоидов), зависящую от формы и размеров соленоидов, диаметра сечения провода соленоидов, значения относительной магнитной проницаемости среды и т. д. Таким образом, ампер воспроизводится через основные единицы - метр, килограмм и секунду. Эталон воспроизводит размер ампера с относительным средним квадратическим отклонением результата измерений, не превышающим 4*10^-6, при относительной систематической погрешности, не превышающей 8*10^-6.

Для поддержания единства измерений можно ограничиваться созданием эталонов только основных величин. Однако для облегчения выполнения этой задачи созданы эталоны производных единиц. Рассмотрим некоторые эталоны производных единиц электрических величин.

В состав государственного эталона вольта входит: мера напряжения на основе эффекта Джозефсона (возникновение напряжения между разделенными тонким слоем диэлектрика двумя сверхпроводниками в высокочастотном электромагнитном поле); группа насыщенных нормальных элементов для хранения размера единицы, компенсатор постоянного тока для сличения нормальных элементов. Эталон воспроизводит размер вольта с относительным средним квадратичным отклонением результата измерения, не превышающим 5*10^-6, при относительной неисключенной систематической погрешности, не превышающей 1*10^-6.

Государственный эталон единицы сопротивления воспроизводит фарад с помощью 10 манганиновых катушек сопротивления с относительным средним квадратическим отклонением результата измерений, не превышающим 1*10^-7, при неисключенной относительной систематической погрешности, не превышающей 5*10^-7.

Государственный эталон единицы емкости воспроизводит фарад с помощью конденсатора с относительным средним квадратическим отклонением результата измерений, не превышающим 7*10^-7, при неисключенной относительной систематической погрешности, не превышающей 13*10^-7.

Государственный эталон единицы индуктивности воспроизводит генри с помощью четырех катушек индуктивности с относительным средним квадратическим отклонением результата измерений, не превышающим 1*10^-5, при неисключенной относительной систематической погрешности, не превышающей 1*10^-5.

1.5. Средства измерений

Средства измерений представляют собой технические средства, служащие для определения размеров измеряемых величин и имеющие нормированные метрологические свойства.

Основными видами средств измерений являются: меры, измерительные приборы, измерительный инструмент, измерительные машины, измерительные установки. К средствам измерений относятся также измерительные принадлежности и измерительные преобразователи, применяемые только совместно с указанными выше измерительными устройствами, для расширения диапазона измерений, повышения точности и чувствительности основных средств измерений, передачи результатов измерения на расстояние и обеспечения техники безопасности. Их метрологические характеристики непосредственно влияют на результат измерений.

1.5.1.Образцовые и рабочие средства измерения

По метрологическому назначению средства измерений делят на образцовые и рабочие. Образцовые средства измерений предназначены для поверки по ним других средств измерений, как рабочих, так и образцовых менее высокой точности. Эта задача чисто метрологического характера, так как именно последовательный ряд образцовых средств измерений различных разрядов обеспечивает передачу размера единицы от эталона до рабочего прибора, а тем самым и сохранение единства мер в стране. Процесс передачи размера единиц от образцовых средств измерений высшей точности рабочим и образцовым средствам измерений называется поверкой, поэтому все образцовые средства измерений являются средствами поверки.

Рабочие средства измерений применяются для измерений, служащих тем или иным конкретным целям в разнообразной деятельности человека.

Сущность разделения средств измерений на образцовые и рабочие лежит не в конструкции и не в точности, а в их назначении.

Одно и то же средство измерений может быть предназначено для практических измерений как в качестве рабочего средства измерения, так и в качестве образцового, другими словами, в качестве средства поверки, а также градуировки. Лишь немногие образцовые средства измерений отличаются по конструкции и некоторым метрологическим характеристикам от рабочих. Но когда средства измерений предназначаются для применения в качестве образцовых, они как бы ставятся в особое положение, изолируются от любых других измерений, кроме проводимых в целях поверки и градуировки.

Однако не каждое средство измерений целесообразно использовать как образцовое. Например, для образцового средства измерений не так важно, насколько велики поправки к его показаниям, как важна стабильность и воспроизводимость его показаний. К образцовым средствам измерений предъявляются более высокие требования в отношении воспроизводимости показаний, чем к аналогичным рабочим средствам измерений.

Запрещение применять образцовые средства измерений для практических измерений является одним из важнейших правил метрологии. Однако им нередко пренебрегают или недооценивают его значение.

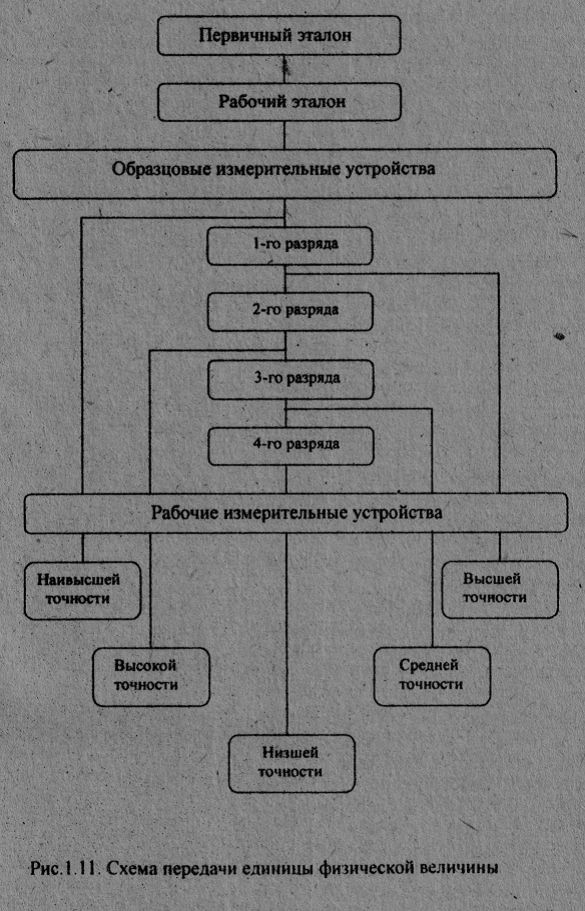
Приведенная на рис.1.11 схема наглядно иллюстрирует это правило.

Каким бы точным ни было средство измерений, применяемое для практических измерений, оно не может применяться для поверки других средств измерений. Само оно должно поверяться по образцовому средству измерений, имеющему более высокую точность.

В свою очередь, к рабочим средствам измерений могут предъявляться свои специфические требования, связанные с условиями их применения.

Средства измерений могут быть в виде мер, измерительных приборов, измерительных установок или измерительных машин.

Мера - тело или устройство, служащее для воспроизведения одного или нескольких известных значений данной величины для целей измерения. Например, гиря; плоскопараллельная концевая мера длины; линейка с делениями; рулетка; измерительная колба; катушка электрического сопротивления; температурная лампа; нормальный элемент; измерительный конденсатор; генератор стандартных сигналов.

Набор мер - совокупность мер, применяемых как отдельно, так и в различных сочетаниях с целью воспроизведения ряда значений величины в определенных пределах. Например, набор гирь; набор плоскопараллельных концевых мер длины; набор измерительных конденсаторов.

Необходимо подчеркнуть, что под набором мер подразумевается не произвольная группа мер с любыми значениями, а совокупность мер с целесообразно выбранным рядом значений.

Магазин мер - набор мер, в котором меры объединены в одно конструктивное целое с устройством для соединения их в различных сочетаниях. Магазины мер широко применяются в электротехнике (магазины сопротивления, магазины индуктивности, магазины емкости).

Ряды значений мер и наборы мер. Рабочие и образцовые меры изготовляют в виде отдельных экземпляров, наборов и магазинов. Даже тогда, когда меры изготовляют в виде отдельных экземпляров, ряд из значений выбирают таким образом, чтобы они обеспечивали переход от одного значения к другому с соблюдением метрологических требований. Например, образцовые катушки электрического сопротивления не только изготовляют, но и применяют отдельно, последовательное или параллельное включение их, как правило, не производится. Тем не менее их изготовляют с номинальными значениями, представляющими собой закономерный ряд и равными 1*10nОм, где n- целые числа или нуль.

При изготовлении наборов или магазинов мер к выбору ряда значений предъявляют особые требования. При этом стремятся наиболее рационально, используя наименьшее число мер, обеспечить возможность получения наибольшего числа сочетаний. Например, набор гирь строится по ряду 1;2;2;5 (в каждом десятичном числовом разряде), что дает возможность воспроизвести все значения от 1 до 10. Такой ряд признан более рациональным, чем ряд 1; 2; 3; 4, содержащий гири четырех размеров вместо трех. Это имеет большое значение при массовом производстве. Кроме того, гири 2 и 3, а особенно 3 и 4 не очень заметно отличаются по размерам, что усложняет пользование ими. Этот же ряд применяется и в магазинах электрических мер со штепсельным переключением. Кроме него, в магазинах мер со штепсельным и рычажным переключением применяется декадная система (1;2;3;...;10)*10 n.

К наборам плоскопараллельных концевых мер длины (называемых для кратности "плитками") предъявляется другое требование: любое значение длины (в заданных пределах) должно воспроизводиться с помощью не более чем четырех - пяти мер. Так, набор из 87 плиток длиной от 0.5 до 100 мм позволяет воспроизводить длину от 0.5 до 340 мм с интервалами 0.005;0.01 и 0.1 мм, применяя не более четырех плиток. Если бы набор плиток был составлен по ряду, подобному набору гирь (1;2;2;5;10;20;...), то для воспроизведения длины 188,88 мм понадобилось бы не четыре, а 13 мер.

Измерительный прибор - средство измерений, в котором измеряемая величина преобразуется в показание или сигнал, пропорциональный измеряемой величине в форме, доступной для непосредственного восприятия наблюдателем. В отличие от меры измерительный прибор не воспроизводит известное значение величины, а измеряемая величина должна подводиться к нему извне, воздействовать на него тем или иным способом.

В состав измерительного прибора входят узлы и детали, служащие для восприятия воздействующей величины, а также для преобразования ее в показания, которые могут быть отсчитаны наблюдателем. Измерительный прибор может содержать также узлы, предназначенные для выполнения дополнительных действий, например, регулирования, сигнализации, дозирования, сортировки, посылки кодированных сигналов и др.

Измерительная установка - совокупность функционально объединенных средств измерений, в которых для преобразования измеряемой величины в сигнал служат одно или несколько измерительных и ряд вспомогательных устройств, расположенных в одном месте.

В состав измерительной установки могут входить измерительные приборы, меры, измерительные приспособления и измерительные преобразователи, а также вспомогательные и регулировочные устройства, источники питания.

Измерительные установки в большинстве случаев обладают большей или меньшей универсальностью, как в отношении номенклатуры измеряемых величин, так и в отношении диапазонов измерений.

Измерительные машины являются измерительными установками более узкого назначения. Как правило, они имеют большие размеры. К измерительным машинам относятся силоизмерительные машины и машины для измерения больших длин.

Средства измерений включают в себя отсчетное устройство, измерительный механизм и измерительные принадлежности.

Отсчетное устройство - часть конструкции средства измерений, предназначенная для отсчитывания значения измеряемой величины. Отсчетное устройство показывающего средства измерений обычно состоит из шкалы и указателя или цифрового преобразователя, отсчетное устройство осуществляет запись ряда значений измеряемой величины на диаграмме; в интегрирующем измерительном устройстве чаще всего применяется счетный механизм. При этом под отсчетом понимается число, отсчитанное при данном измерении по отсчетному устройству либо полученное путем счета последовательных отметок или сигналов. Показание же средства измерений - это значение измеряемой величины, устанавливаемое по отсчету, например, путем умножения на цену деления.

Измерительный механизм, или измеритель, - часть конструкции средства измерений, включающая органы, воспринимающие измеряемую величину и преобразующие ее действие в показания отсчетного устройства. Измерительный механизм состоит из элементов, взаимодействие которых вызывает их взаимное перемещение. Нередко воспринимающий орган измерительного механизма называют чувствительным элементов.

Измерительная принадлежность - устройство, применяемое при измерении и служащее для поддержания надлежащих значений измеряемых или влияющих на измерение величин или для повышения чувствительности измерительных устройств. Примерами измерительных принадлежностей являются: усилитель, лупа, термостат для поверки термометров. Характерная особенность измерительных принадлежностей заключается в том, что они служат для улучшения условий измерений, не изменяя непосредственно диапазонов измерения.

Измерительное средство иногда может быть представлено измерительным преобразователем.

Измерительный преобразователь - средство измерений, служащее для преобразований измеряемой величины в величину, действующую на измерительный механизм.

Далеко не всегда целесообразно, а во многих случаях и невозможно строить средство измерений так, чтобы измеряемая величина непосредственно воздействовала на его измерительную часть или на измерительный механизм. Обычно измеряемая величина подвергается предварительному преобразованию, которое может быть многоступенчатым, и измерительный механизм измеряет уже преобразованную величину, находящуюся в определенной зависимости от измеряемой величины.

1.5.2. Измерительные преобразователи

Многоступенчатое преобразование измеряемой величины приобретает в современной измерительной технике все большее значение и преследует самые разнообразные цели. Поэтому возникла необходимость классифицировать измерительные преобразователи по их назначению и функциям, которые они выполняют.

Но прежде чем рассматривать различные виды измерительных преобразователей, остановимся на одной особенности измерительных преобразователей. Выше подчеркивалось, что измерительные преобразователи не являются чем-то самостоятельным. Киловольтметр, например, имеет измерительный механизм, шкала которого проградуирована в киловольтах.

В действительности, измерительный механизм измеряет напряжение не более 100В. Его соединяют с измерительным трансформатором напряжения, который и преобразует измеряемое напряжение, например 110кВ, в напряжение 110В. Ни измеритель на 100В со шкалой в киловольтах, ни трансформатор напряжения, каждый в отдельности, не могут измерять напряжение 110кВ. Только в совокупности они представляют собой средство измерений - киловольтметр.

Несмотря на то, что измерительный трансформатор по своим размерам может во много раз превосходить измеритель, он является составной частью измерительного устройства. Но, с другой стороны, измерительные преобразователи могут применяться не только для измерений, но и для других целей, где преобразование одной величины в другую с известной точностью может иметь значение, например, в автоматических устройствах. В частности, к упомянутому измерительному трансформатору напряжения может быть подключена автоматическая система защиты линии передачи.

Приемный или первичный преобразователь - измерительный преобразователь, к которому подведена измеряемая величина, т.е. он является первым в измерительной цепи.

Для приемных преобразователей характерно то, что на них воздействует непосредственно измеряемая величина. Физическая величина, в которую преобразует измеряемую величину приемный преобразователь, может быть подведена к измерительному механизму, может быть подана на другой преобразователь или использована, например, для целей телеизмерений.

К приемным преобразователям могут быть отнесены такие одноступенчатые преобразователи, как термопары или сужающие устройства расходомеров, основанных на принципе измерения перепада давления в потоке жидкости или газа.

Из многоступенчатых преобразователей можно назвать приемный преобразователь термохимического газоанализатора.

Передающий преобразователь - измерительный преобразователь, служащий для преобразования показаний измерительного механизма или величины, полученной от приемного преобразователя, в другую физическую величину для передачи ее на расстояние.

Передающий преобразователь может быть аналогично приемному одно- и многоступенчатым.

Для этой группы преобразователей характерным является назначение величины, образуемой на его "выходе".

Очевидно, что преобразователь может одновременно выполнять функции приемного и передающего.

Приемные и приемно-передающие преобразователи часто называют датчиками.

Масштабный преобразователь - измерительный преобразователь, служащий для изменения в определенное число раз значения одной из величин, действующих в цепи измерительного прибора, без изменения ее физической природы. К числу таких преобразователей относятся уже упоминавшиеся измерительные трансформаторы напряжения, а также трансформаторы тока, измерительные усилители и т.п. Масштабные преобразователи чаще всего являются одним из видов приемных преобразователей, хотя могут служить и передающими.

Первичный измерительный механизм (первичный измеритель) - измерительный механизм, служащий для измерения величины, создаваемой приемным преобразователем. К числу таких механизмов относятся, например, дифманометры расходомеров переменного перепада давления.

Вторичный измерительный механизм (вторичный измеритель) - механизм, служащий для измерения величины, получаемой от передающего преобразователя.Вторичным измерителем может служить автоматический потенциометр, измеряющий электрическое напряжение, создаваемое передающим преобразователем, например, передающим преобразователем расхода жидкости или газа.

Измерительные устройства - наименование категории средств измерений, охватывающей измерительные приборы и измерительные преобразователи.

1.5.3. Погрешности измерительных средств

При пользовании измерительными средствами необходимо различать определенные группы их погрешностей.

Погрешность измерительного прибора - алгебраическая разность между показанием прибора и действительным значением измеряемой величины (определенным более точным методом).

Погрешности измерительных приборов являются одной из важнейших метрологических характеристик приборов. Они отражают несовершенство измерительного устройства и возникают вследствие многих причин, а именно: несовершенства конструкции, материалов и технологии изготовления, неудовлетворительного качества изготовления, погрешности градуировки и др.

Погрешность меры - алгебраическая разность между номинальным и действительным значениями меры. Для многозначной меры погрешности при данном показании определяется как разность между показанием и действительным значением измеряемой величины.

Номинальное значение меры - значение данной физической величины, обозначенное на мере (или на ее футляре). Это определение относится главным образом к однозначным мерам. Для многозначных мер и магазинов мер - это "показание меры", под которым подразумевают значение величины, воспроизводимой мерой, устанавливаемое по отсчету.

При сравнении приведенного определения понятия погрешности меры с общим определением этого понятия следует отметить, что номинальное значение меры соответствует измеренному значению величины x. На первый взгляд такое сравнение кажется странным. Но стоит вспомнить, что номинальное значение - это не что иное, как показание, а действительное значение величины, воспроизводимой мерой, отличается от него и ближе к истинному значению этой величины.

Если, например, номинальное значение массы гири 1кг, а ее действительное значение 0,999кг, то погрешность гири +0.001кг.

Необходимо помнить, что отклонение номинального значения меры от действительного - величина, противоположная по знаку погрешности меры.

Вариация показаний - наибольшая разность между показаниями, полученными при многократно повторенных измерениях одной и той же величины.

Приведенная погрешность - погрешность, выраженная в процентах от какого-либо определенного значения, в большинстве случаев от диапазона измерения, определяемого пределами рабочей части шкалы измерительного устройства. Когда нижний предел измерения равен нулю, приведенная погрешность выражается в процентах от верхнего предела измерения данного устройства. Точность ряда средств измерений с различными пределами измерения может сопоставляться только по их приведенным погрешностям. Поэтому классы точности многих средств измерений определяются по наибольшим допускаемым приведенным погрешностям. Однако именно они являются часто причиной грубых ошибок в оценке погрешностей измерений.

Относительная погрешность меры или измерительного прибора - погрешность, которая выражается отношением погрешности меры или измерительного прибора к значению самой измеряемой величины, а не отношением ее к какому-либо постоянному значению, как это имеет место в приведенной погрешности.

Поправка - значение, которое прибавляется алгебраически к результату измерения, полученному с помощью средства измерений, для исключения систематических погрешностей. По знаку поправка противоположна погрешности.

Для однозначных мер, поправка по знаку совпадает с отклонением номинального значения меры от ее действительного значения (т.е. с разностью между действительным и номинальным значениями меры).

1.6. Поверка средств измерений

Поверкой мер и измерительных приборов называют совокупность действий, выполняемых для определения или оценки погрешностей средства измерений. Цель, которую в первую очередь преследует поверка, - выяснить, соответствуют ли точностные характеристики приборов регламентированным значениям и пригодно ли средство измерений к применению.

Иногда поверку пытаются ограничить небольшим участком диапазона измерений и заданием точности в зависимости от конкретного случая применения прибора. Например, амперметр поверяют только при силе тока 4 А, что соответствует устойчивому режиму работы определенной установки. Такая поверка не может быть рекомендована, так как при выходе из строя данного амперметра для его замены необходимо будет подвергнуть такой же специализированной поверке другой амперметр. В то же время поверенные таким образом средства измерений непригодны для применения на других рабочих местах. Поэтому, как правило, пользуются средствами измерений, погрешности которых определены для всей шкалы и соответствуют требуемой точности измерений. В этом случае замена вышедшего из строя средства измерений не составляет труда. Кроме того, такое средство измерений может быть применено в любом другом месте, где требования к нему и условия его применения не выходят за рамки, установленные соответствующими нормами (стандартами).

При поверке средств измерений, предназначенных для применения без поправок, определяют, не выходят ли их погрешности (а также некоторые другие показатели) за установленные пределы, не превышают ли они допускаемые значения. При поверке средств измерений, применяемых с учетом поправок к их показаниям, задача усложняется, так как необходимо определять значения погрешностей. Повышаются требования к образцовым средствам измерений, процесс поверки становится более трудоемким.

Какое значение имеет определение погрешности, можно наглядно показать на примере плоскопараллельных концевых мер длины (“плиток"). При изготовлении плиток их длину доводят до номинального" значения, указанного на каждой плитке, с большей или меньшей точностью. По оставшемуся отклонению от номинального значения плитки делят на классы: чем меньше это отклонение, тем выше класс (тем меньше номер класса). Например, для плитки 2-го класса с номинальным размером 130 мм допускается отклонение +0,001 мм. Если при измерении такой погрешностью можно пренебречь, то длину плитки принимают равной 130 мм, хотя действительная ее длина может быть любой между 129,999 и 130,001 мм. Однако с помощью этой можно провести более точные измерения, если определить действительную ее длину.

Если длина плитки номинальным размером 130 мм определена с погрешностью, не превышающей 0,0004 мм, то ее длина может оказаться, например, равной 130,0005+0,0004 мм. Длину плитки при ее использовании принимают равной 130,0005 мм. Если погрешность определения размера плитки не превышает 0,00012 мм, длина ее может оказаться равной, например, 129,99945+0,00012 мм. За действительную длину плитки принимают 129,99945 мм. Естественно, что в каждом из описанных случаев к образцовым средствам измерений и методам поверки предъявляют различные требования, причем эти требования тем выше, чем выше необходимая точность.

Поверка средств измерений имеет большое значение, выходящее далеко за рамки данной лаборатории, института, предприятия. Обеспечивая единство мер, как одно из условий обеспечения единства измерений во всех звеньях народного хозяйства страны, она обеспечивает тем самым бесперебойное и безотказное взаимодействие этих звеньев максимально эффективное использование результатов их работы. Известно немало случаев, когда из-за нарушения единства мер, несопоставимости показаний средств измерений оказалось невозможным наладить работу важных и сложных установок.

Обеспечение взаимозаменяемости изделий, деталей и узлов зависит в первую очередь от правильной и своевременной поверки средств измерений.

Большое значение имеет поверка средств измерений и в международном масштабе. Без обеспечения международного единства мер и единства измерений практически невозможно наладить торговлю, культурный и научный обмен, если объекты торговли и обмена имеют характеристики, определяемые путем измерений.

Поверка средств измерений является по существу одним из звеньев многоступенчатого процесса передачи размера единицы от эталона до рабочего средства измерений. Именно связь с эталоном является необходимым условием повсеместного единства мер, единства измерения. Связь эта осуществляется ступенями, причем, если идти от эталона, каждая следующая ступень по точности ниже предыдущей. При применении средств измерений в рабочих условиях эта связь осуществляется как бы в обратном направлении: от применяемого им средства измерений вверх до эталона. Быть уверенным в правильности показаний рабочего средства измерения можно, только поверив его с помощью более точного образцового средства измерений.

Чтобы удостовериться в том, что погрешности образцового средства измерений малы настолько, насколько это необходимо для поверки рабочего средства измерений, образцовое средство измерений в свою очередь подвергается поверке с помощью еще более точного образцового средства измерений и так далее до эталона.

1.6.1. Выбор образцового средства измерений

Во сколько раз погрешности образцового средства измерений должны быть меньше, чем допускаемые погрешности рабочего средства измерений? От ответа на этот вопрос зависит выбор образцового средства измерений. Однако до настоящего времени однозначного ответа на этот вопрос не дано. Это объясняется тем, что дать такой ответ невозможно.

При выборе образцовых средств измерений следует учитывать не только погрешности, но также и степень достоверности определения погрешностей поверяемых и образцовых средств измерений. При этом возникают существенные трудности, так как применить математический аппарат теории вероятностей безоговорочно нельзя. Та погрешность, которой обычно характеризуется точность прибора, содержит и случайные, и систематические погрешности, и, кроме того, она может изменяться под действием внешних причин.

Требования, предъявляемые к образцовым измерениям, в некоторой степени противоречивы. С одной стороны, чем они точнее, тем больше уверенность в правильности определения погрешностей поверяемого средства измерений. С другой стороны, более точное средство измерений дорого, эксплуатация его сложна, оно требует бережного обращения, нормальный режим его применения более ограничен, его необходимо поверять чаще, чем средство измерений менее точное, но более надежное.

Граница высшего уровня точности образцового средства измерений, при которой обеспечивается надежная поверка, определяется сравнительно просто. Как правило, значение погрешности дается в виде числа с одной или максимум двумя значащими цифрами, причем вторая цифра равна 5, например 1; 0,1;0,25% и т.д. Можно считать, что погрешность средства измерений определена достаточно достоверно, если погрешность образцового средства измерений не превышает в десять раз меньшее значение. Например, тогда, когда для поверки измерительного устройства с допускаемой погрешностью 1% применяется образцовое измерительное устройство, погрешности которого не превышают 0,1%.

Сказанное относится к случаю поверки средств измерений, для которых не требуется указание поправок. При определении поправок к показаниям средств измерений предельная допускаемая погрешность поверяемых средств измерений не может служить критерием для определения необходимой точности образцового средства измерений. Таким критерием является точность, с которой требуется определить поправки. Эта точность ограничивается степенью постоянства показаний средств измерений, возможной точностью отсчета и некоторыми другими характеристиками, присущими поверяемым средствам измерений.

Пример. Для электроизмерительного показывающего прибора класса 0,5 допускаемая погрешность составляет +0,5% от верхнего предела измерения (конечного значения рабочей части шкалы). Шкала прибора имеет 100 делений, погрешность отсчета показаний может быть снижена до +0,1 деления, т.е. до +0,1%. Вариации показаний практически не обнаруживаются, т.е. они не превышают 0,1 деления. К такому прибору можно дать поправки, при пользовании которыми погрешности не будут превышать +0,1 деления (+0,1%). Для поверки прибора (при отношении погрешностей 1:10) следует применить образцовый измерительный прибор, погрешности которого не превышают +0,01%. Если же вариации показаний поверяемого прибора достигают 0,3 деление (0,3%), введение поправок теряет смысл и поверку можно провести с по