Константа скорости реакции k зависит от природы реагирующих веществ и от температуры, но не зависит от их концентраций

Уравнение (1), связывающее скорость реакции с концентрацией реагирующих веществ, называется кинетическим уравнением реакции. Если опытным путем определено кинетическое уравнение реакции, то с его помощью можно вычислять скорости при других концентрациях тех же реагирующих веществ.

Влияние температуры.

Зависимость скорости реакции от температуры определяется правилом Вант-Гоффа:

При повышении температуры на каждые 10о скорость большинства реакций увеличивается в 2-4 раза.

Математически эта зависимость выражается соотношением

vt 2 = vt 1 γ,

где vt 1, vt 2 - скорости реакции соответственно при начальной (t 1) и конечной (t 2) температурах, а γ - температурный коэффициент скорости реакции, который показывает, во сколько раз увеличивается скорость реакции с повышением температуры реагирующих веществ на 10°.

Правило Вант-Гоффа является приближенным и применимо лишь для ориентировочной оценки влияния температуры на скорость реакции. Температура влияет на скорость химической реакции, увеличивая константу скорости.

Уравнение Аррениуса. Зависимость скорости реакции от температуры обычно описывают уравнением Аррениуса, которое в простейшем виде можно записать как v = v0 a = v0e–Ea/RT, где v0 – скорость, которую имела бы реакция при нулевой энергии активации (фактически это частота столкновений в единице объеме). Поскольку v0 слабо зависит от температуры, все определяет второй сомножитель – экспоненциальный: с увеличением температуры этот сомножитель быстро увеличивается, причем тем быстрее, чем больше энергия активации Еа. Указанная зависимость скорости реакции от температуры называется уравнением Аррениуса, оно – одно из важнейших в химической кинетике.

• 53. Исследование механизма химической реакции. Понятия: простые (элементарные) реакции,

порядок, молекулярность, сложные реакции разного типа. Привести примеры. Лимитирующая стадия химического процесса.

Сложные реакции. Стехиометрич. ур-ние, как правило, не отражает истинного механизма реакции. Так, газофазная термически активируемая неразветвленная цепная р-ция Н2 + Вr2 2НВr состоит из след.простых стадий: термич. инициирование Вr2; продолжения цепи + Н2НВr +; + + Вr2НВr +; + НВr Н2 +; обрыв цепи + + Вr2. Скорость процесса описывается сложным ур-нием, включающим константы скорости всех простых стадий и концентрации в-в Вr2, Н2 и НВr. Другой пример -нуклеоф. замещение при атоме С, соответствующее стехиометрич. ур-нию RX + Y-RY+X-, к-рое в зависимости от природы реагентов и р-рителя может идти по двум разл. механизмам SN2 и SN1 (см. Нуклеофильные реакции).

Характеризуя механизм сложной р-ции, часто указывают на его главную отличит.особенность: ионный механизм реакции, когда наиб. характерно участие в отдельных стадиях ионов; радикальный механизм реакции, радикально-цепной, нуклеоф. или элект-роф. замещение и т.п. Иногда механизм реакции называют по имени исследователя, его предложившего и доказавшего, напр. механизм реакции Налбандяна - Воеводского для взаимод. Н2 с О2, механизм реакции Бендера для замещения при карбонильном атоме С и т. п.

Установление механизма сложной р-ции начинается с изучения изменения во времени концентраций исходных в-в и, если возможно, промежут. в-в, определения порядков р-ции по отдельным реагентам при широком диапазоне вариации условий (т-ра, начальные парциальные и суммарные давления для газофазных р-ций; исходные и суммарные концентрации реагентов, природа р-рителя для р-ций в р-рах). На основе полученных данных предлагают одну или неск. возможных схем р-ции и составляют системы дифференц. ур-ний. При решении этих систем с помощью ЭВМ различают прямую и обратную задачи. В прямой задаче константы скорости и константы равновесия отд. простых стадий, полученные экспериментально или оцененные независимым путем, задают ЭВМ, к-рая численно или графически представляет результаты решения системы ур-ний в виде кинетич. кривых сложной р-ции. Затем эти кривые сопоставляют с эксперим. данными. В обратной задаче, существенно более сложной, ЭВМ на основе схемы р-ции и всего объема кинетич. сведений "выдает" константы скорости отдельных стадий. Чем сложнее кинетич. закономерности (смена порядка р-ций, запределивание кинетич. кривых, появление на них изломов и др. особенностей), тем больше возможностей, сопоставляя эксперим. данные и результаты расчетов, дискриминировать ту или иную схему в поисках истинного механизма реакции.

Важную роль в установлении механизма реакции играет исследование природы продуктов и промежут. в-в методами УФ, ИК и гамма-резонансной спектроскопии, ЭПР, ЯМР, масс-спект-рометрии, хим. поляризации ядер, электрохим. методами и т.п. Разрабатываются способы получения и накопления высокоактивных промежут. продуктов: ионов, радикалов, возбужденных частиц с целью непосредственного изучения их реакц. способности. Для получения констант скорости тех стадий сложной р-ции, в к-рых участвуют высокоактивные частицы, информативно моделирование этих стадий в специальных ("чистых") условиях, напр. путем проведения р-ций при низких т-рах (до 100-70 К), в ионном источнике масс-спектрометра высокого давления, в ячейке спектрометра ион-циклотронного резонанса и т.п. При изучении гетерогенно-каталитич. р-ций важно независимое исследование адсорбции всех участвующих в р-ции в-в на пов-сти катализатора, изучение спектров адсорбир. частиц в оптич. и радиочастотном диапазонах, а также установление их природы физ. и физ.-хим. методами (рентгеновская и УФ фотоэлектронная спектроскопия, оже-спектроскопия, спектроскопия энергетич. потерь электронов и др.).

Элементарные реакции. Для установления механизма реакции привлекают как теоретич. методы (см. Квантовая химия, Динамика элементарного акта), так и многочисленные эксперим. методы. Для газофазных р-ций это - молекулярных пучков метод, масс-спектрометрия высокого давления, масс-спектро-метрия с хим. ионизацией, ионная фотодиссоциация, ион-циклотронный резонанс, метод послесвечения в потоке, лазерная спектроскопия-селективное возбуждение отдельных связей или атомных групп молекулы, в т.ч. лазерно-индуцированная флуоресценция, внутрирезонаторная лазерная спектроскопия, активная спектроскопия когерентного рассеяния. Для изучения механизма реакции в конденсир. средах используют методы: ЭПР, ЯМР, ядерный квадрупольный резонанс, хим. поляризацию ядер, гамма-резонансную спектроскопию, рентгенo- и фотоэлектронную спектроскопию, р-ции с изотопными индикаторами (мечеными атомами) и оптически активными соед., проведение р-ций при низких т-рах и высоких давлениях, спектроскопию (УФ, ИК и комбинационного рассеяния), хемилюминесцентные методы, полярографию, кинетич. методы исследования быстрых и сверхбыстрых р-ций (импульсный фотолиз, методы непрерывной и остановленной струи, температурного скачка, скачка давления и др.). Пользуясь этими методами, зная природу и строение исходных и конечных частиц, можно с определенной степенью достоверности установить структуру переходного состояния (см. Активированного комплекса теория), выяснить, как деформируется исходная молекула или как сближаются исходные частицы, если их несколько (изменение межатомных расстояний, углов между связями), как меняется поляризуемость хим. связей, образуются ли ионные, свободнорадикальные, триплетные или др. активные формы, изменяются ли в ходе р-ции электронные состояния молекул, атомов, ионов.

Проведение реакции в условиях, когда концентрация одного из реагентов много меньше концентрации другого (других) и скорость реакции зависит от концентрации только этого реагента, используется для определения частных порядков реакции – это т.н. метод избыточных концентраций или метод изолирования Оствальда. Порядок реакции по данному веществу определяется одним из перечисленных ниже методов.

Графический метод заключается в построении графика зависимости концентрации реагента от времени в различных координатах. Для различных частных порядков эти зависимости имеют следующий вид:

Если построить графики этих зависимостей на основании опытных данных, то лишь одна из них будет являться прямой линией. Если, например, график, построенный по опытным данным, оказался прямолинейным к координатах lnC = f(t), то частный порядок реакции по данному веществу равен единице.

Метод подбора кинетического уравнения заключается в подстановке экспериментальных данных изучения зависимости концентрации вещества от времени в кинетические уравнения различных порядков. Подставляя в приведённые в таблице уравнения значения концентрации реагента в разные моменты времени, вычисляют значения константы скорости. Частный порядок реакции по данному веществу равен порядку того кинетического уравнения, для которого величина константы скорости остаётся постоянной во времени.

Метод определения времени полупревращения заключается в определении t1/2 для нескольких начальных концентраций. Как видно из приведённых в таблице уравнений, для реакции первого порядка время полупревращения не зависит от Co, для реакции второго порядка – обратно пропорционально Co, и для реакции третьего порядка – обратно пропорционально квадрату начальной концентрации.

По характеру зависимости t1/2 от Co нетрудно сделать вывод о порядке реакции по данному веществу. Данный метод, в отличие от описанных выше, применим и для определения дробных порядков.

2.1.6 Молекулярность элементарных реакций

Элементарными (простыми) называют реакции, идущие в одну стадию. Их принято классифицировать по молекулярности:

Молекулярность элементарной реакции – число частиц, которые, согласно экспериментально установленному механизму реакции, участвуют в элементарном акте химического взаимодействия.

Мономолекулярные – реакции, в которых происходит химическое превращение одной молекулы (изомеризация, диссоциация и т. д.):

I2 ––> I• + I•

Бимолекулярные – реакции, элементарный акт которых осуществляется при столкновении двух частиц (одинаковых или различных):

СН3Вr + КОН ––> СН3ОН + КВr

Тримолекулярные – реакции, элементарный акт которых осуществляется при столкновении трех частиц:

О2 + NО + NО ––> 2NО2

Реакции с молекулярностью более трёх неизвестны.

Для элементарных реакций, проводимых при близких концентрациях исходных веществ, величины молекулярности и порядка реакции совпадают. Тем не менее, никакой чётко определенной взаимосвязи между понятиями молекулярности и порядка реакции не существует, поскольку порядок реакции характеризует кинетическое уравнение реакции, а молекулярность – механизм реакции.

54. Химическое равновесие. Обратимые и необратимые химические реакции. Константа

равновесия. Закон действующих масс для равновесия. Принцип Ле-Шателье.

Химическим равновесием называется такое состояние химической системы, при котором количества исходных веществ и продуктов не меняются со временем.

Реакции, которые протекают только в одном направлении и завершаются полным превращением исходных реагирующих веществ в конечные вещества, называются необратимыми.

Примером такой реакции может служить разложение хлората калия (бертолетовой соли) при нагревании:

2ClO 3 = 2KCl + 3O 2 ↑

Реакция прекратится тогда, когда весь хлорат калия превратится в хлорид калия и кислород. Необратимых реакций не так много. Большинство реакций являются обратимыми.

Обратимыми называются такие реакции, которые одновременно протекают в двух взаимно противоположных направлениях.

В уравнениях обратимых реакций между левой и правой частями ставят две стрелки, направленные в противоположные стороны. Примером такой реакции может служить синтез аммиака из водорода и азота:

∆H = -46,2 кДж / моль

В технике обратимые реакции, как правило, невыгодны. Поэтому различными методами (изменение температуры, давления и др.) их делают практически необратимыми.

Необратимыми называются такие реакции, при протекании которых:

1) образующиеся продукты уходят из сферы реакции - выпадают в виде осадка, выделяются в виде газа, например

ВаСl2 + Н 2SО 4 = ВаSО4↓ + 2НСl

Na 2CO 3 + 2HCl = 2NaCl + CO2 ↓ + H2O

2) образуется малодиссоциированное соединение, например вода:

НСl + NаОН = Н2О + NаСl

3) реакция сопровождается большим выделением энергии, например горение магния

Mg + 1/2 О2 = МgО, ∆H = -602,5 кДж / моль

В уравнениях необратимых реакций между левой и правой частями ставится знак равенства или стрелка.

Конста́нта равнове́сия — величина, определяющая для данной химической реакции соотношение между термодинамическими активностями (либо, в зависимости от условий протекания реакции, парциальными давлениями, концентрациями или фугитивностями) исходных веществ и продуктов в состоянии химического равновесия (в соответствии с законом действующих масс). Зная константу равновесия реакции, можно рассчитать равновесный состав реагирующей смеси, предельный выход продуктов, определить направление протекания реакции.

Константа равновесия.

Важнейший параметр, характеризующий обратимую химическую реакцию – константа равновесия К. Если записать для рассмотренной обратимой реакции A + D C + D условие равенства скоростей прямой и обратной реакции в состоянии равновесия – k1[A]равн[B]равн = k2[C]равн[D]равн, откуда [C]равн[D]равн/[A]равн[B]равн = k1/k2 = К, то величина К называется константой равновесия химической реакции.

Итак, при равновесии отношение концентрации продуктов реакции к произведению концентрации реагентов постоянно, если постоянна температура (константы скорости k1 и k2 и, следовательно, константа равновесия К зависят от температуры, но не зависят от концентрации реагентов). Если в реакции участвуют несколько молекул исходных веществ и образуется несколько молекул продукта (или продуктов), концентрации веществ в выражении для константы равновесия возводятся в степени, соответствующие их стехиометрическим коэффициентам. Так для реакции 3H2 + N2 2NH3 выражение для константы равновесия записывается в виде K = [NH3]2 равн/[H2]3равн[N2]равн. Описанный способ вывода константы равновесия, основанный на скоростях прямой и обратной реакций, в общем случае использовать нельзя, так как для сложных реакций зависимость скорости от концентрации обычно не выражается простым уравнением или вообще неизвестна. Тем не менее, в термодинамике доказывается, что конечная формула для константы равновесия оказывается верной.

Для газообразных соединений вместо концентраций при записи константы равновесия можно использовать давление; очевидно, численное значение константы при этом может измениться, если число газообразных молекул в правой и левой частях уравнения не одинаковы.

Чтобы легче понять принцип Ле Шателье, рассмотрим простую химическую реакцию. Два вещества (реактивы) взаимодействуют друг с другом, в результате взаимодействия образуется третье вещество (продукт), которое стремится к расщеплению на исходные вещества. Это можно изобразить в виде следующего уравнения:

A + B <—> C

Двойная стрелка обозначает обратимую реакцию. При протекании прямой реакции слева направо происходит образование вещества C из веществ A и B. В случае обратной реакции (справа налево) вещество C расщепляется на вещества A и B. Когда эта система находится в химическом равновесии, скорости прямой и обратной реакций одинаковы — в одной точке данной системы образуется молекула вещества C, а где-то в другом месте другая молекула вещества С распадается.

Если в систему добавить избыток вещества A, равновесие временно нарушится, так как вырастет скорость образования вещества C. Но чем быстрее будет расти концентрация вещества C, тем быстрее оно будет расщепляться — пока снова не будет достигнуто равновесие между прямой и обратной реакциями. Тогда скорость образования вещества C из веществ A и B сравняется со скоростью расщепления вещества С на вещества A и B.

Действие принципа Ле Шателье можно проследить на примере изменения химического состава дождя или растворения шипучей антацидной (снижающей кислотность желудочного сока) таблетки в воде. В обоих случаях в химической реакции участвуют углекислый газ (CO2), вода(H2O) и угольная кислота (H2CO3):

CO2 + H2O <—> H2CO3

Когда дождевая капля попадает в воздух, она поглощает углекислый газ, и концентрация в левой части реакции возрастает. Для поддержания равновесия образуется большее количество угольной кислоты. В результате дождь становится кислотным (см. Кислотный дождь). Добавление углекислого газа смещает равновесие реакции вправо. Противоположная реакция происходит при опускании в воду таблетки антацида (вещества, нейтрализующего кислоту). Бикарбонат натрия (антацид) вступает в реакцию с водой, и образуется угольная кислота, что приводит к увеличению концентрации вещества в правой части реакции. Чтобы восстановилось равновесие, угольная кислота разлагается на воду и углекислый газ, который мы и наблюдаем в виде пузырьков.

55. Теории переходного состояния и активного комплекса. Энергия активации и уравнение Аррениуса

В основе теории лежит закон действия масс и необх-сть активных столкновений, но сам процесс столкновения рассматривается более детально с точки зрения структурных и энерг-х уменьшений.

Рассмотрим процесс вида: А+MN=AM+N

При достаточном сближении атома А с молекулой MN,начинает ослаблять связь M-N и одновременно начинается формирование связи А-M, в результате образуется активный комплекс/переходное состояние A-M-N, в котором за счет взаимного влияния частиц и ослабления валентных связей.

Атом М в равной степени принадлежит атомам А и N, в дальнейшем наиболее вероятным течением процесса является разрыв связи M-N и образование молекулы А-М:

А+MN=A-M-N=A-M+N (1)

Мерой относительной устойчивости реакции веществ: А+MN и пер.состояние A-M-N является константой равновесия К*. От обычной константы она отличается величиной и размерностью. Само первое состояние: A-M-N также нельзя отождествлять с промежуточными хим. соединениями. Время его существования ничтожно, оно короче времени соударения, его структура составляет максимум потенциальной энергосистемы. Образование активированного комплекса в реакции требует определенной энергии активации, распад же его происходит самопроизвольно, т.е. при своем движении по пути реакции реагентная система проходит через энергетический барьер. Скорость реакции 1 равно числу активных комплексов, проходящих в единицу времени через энергетический барьер в направлении хода реакции. Она определяется как произведение так называемой линейной концентрации С* активного комплекса вдоль пути реакции.

Средняя скорость движения этого комплекса по данному пути

W=КС1С2=χС*V.

- С1 и С2 концентрация веществ: А и МN

Из последнего выражения => что константа скорости:

K=(χ(C*)V)/(C1*C2) (2) C*/(C1C2)=К* (3) К=(К*)χV (4)

V и χ вычисляются по уравнениям молекулярно-кинетической теории газов и квантовой теории. К* определяется методами статистической термодинамики на основании спектроскопии данных.

К= χ((RT)/(NAh))e-ΔF*/RT (5) ΔF*=ΔU*-TΔS* (6) K= χ((RT)/(NAh))e-ΔU*/RTeΔS*/R

ΔF* -изменение энергии Гельм-Гольца в процессе активации

NA –число Авогадро

h – постоянная Пианка

ΔU* -изменение внутренний энергии при активации

ΔS* -изменение энтропии при активации

Изменение внутренней энергии при активации:

ΔU=E

K=χ((RT)/(NAh))e-E/RT * eΔS*/R

Сравним полученное выражение с уравнением для константы скорости в теории активных столкновений:

K=PZ0e-E/RT

В результате сравнения получим:

PZ0=χ((RT)/(NA*h))*eΔS*/R

Отсюда следует, что стерический фактор Р действительно является вероятной характеристикой, так как определяется изменением энтропии в процессе образования активного комплекса. Возможность вычислять ΔS* и стерического фактора Р придают особую ценность теории первого состояния.

Энергия активации в элементарных реакциях, минимальная энергия реагентов (атомов, молекул и других частиц), достаточная для того, чтобы они вступили в хим. реакцию, т. е. для преодоления барьера на поверхности потенциальной энергии, отделяющего реагенты от продуктов реакции.

Более точную зависимость константы скорости реакции от температуры устанавливает уравнение Аррениуса:

k = k0 exр (- Еа \RT), где Еа- аррениусовская или опытная энергия активации; Т – абсолютная температура; R – универсальная газовая постоянная; k0 – предэкспоненциальный множитель, мало зависящий от температуры.

уравнение Аррениуса часто представляют в логарифмической форме:

lnk = lnk0 – Е0\RT удобной для графического определения энергии активации. Энергию активации (энтальпию активации) можно вычислить по значениям константы скорости, измеренным при нескольких разных температурах. По экспериментальным данным строят график зависимости lnk от1 \T тангенс угла наклона полученной прямой линии к оси Х равен (-Еа\R) стр 257

Энергию активации можно также оценить, если известны константы скорости при двух температурах Т1и Т2. Тогда для каждой температуры можно записать

lnk1 = lnk0 – Е0\RT1

lnk2= lnk0 – Е0\RT2 вычитая из второго уравнения первое, получают:

lnk2 – lnk1 = (lnk0 – Е0\RT2) – (lnk0 – Е0\RT1)

отсюда: ln(k2\k1)= Еа (Т2–T1)\RТ2Т1

выражение для энергии активации имеет вид:

Еа = RТ2Т1 ln(k2\k1)\(Т2–T1) где Еа - Дж\ моль

Энергия активации представляет собой избыток энергии (в расчете на 1 моль) по сравнению со средней энергией молекул при данной температуре, необходимый для того, чтобы реагирующие частицы могли вступить в химическую реакцию и определяется свойствами реагирующих частиц, их энергетическим состоянием. Чтобы написать уравнение Аррениуса в дифференциальной форме, дифференцируют логарифмическую форму по температурах и получают:

d lnk\dТ = Еа\RТ2 чем больше энергия активации, тем быстрее увеличивается константа скорости реакции с возрастанием температуры.

В настоящее время разработаны две основные теории, объясняющие кинетику протекания элементарных реакций.

Теория активных столкновений. Эта теория базируется на двух общих положениях.:

-реакция осуществляется в момент столкновения двух молекул А и В;

-столкновение приводит к химическому превращению только в том случае, когда молекулы А и В обладают достаточно большим запасом энергии. Эта энергия необходима для преодоления сил отталкивания, проявляющихся при сближении любых валентно-насыщенных молекул. Если относительная скорость движения молекул А и В (вдоль линии, соединяющей центры) достаточно велика, молекулы могут сблизится до таких малых расстояний, на которых возможно перераспределение химических связей в реагентах.

В теории активированного комплекса для любой элементарной реакции предполагается, что начальная конфигурация атомов переходит в конечную в результате непрерывного изменения межъядерных расстояний.

Например в ходе элементарной реакции А + ВС -> АВ + С сближаются атомы А и В. Расстояние А-В (R1) уменьшается, а расстояние В-С (R2) увеличивается.

Установлено, что подобные реакции осуществляются с наименьшей затратой энергии, если атомы располагаются на одной линии, соединяющей их центры. Тогда ход реакции можно описать, использую всего два межъядерных расстояния R1 и R2. В процессе непрерывного изменения межъядерных расстояний всегда образуется промежуточная конфигурация А...В...С, в которой связь В-С уже ослаблена, но еще не полностью разорвана, а связь А-В уже начала образовываться. Такая конфигурация является критической для данной реакции. Продукты реакции могут появиться только при условии образования этой конфигурации, которая называется переходным состоянием или активированным комплексом.

• 56. Явление катализа. Катализаторы и каталитические системы. Энергетическая диаграмма

хода реакции с участием катализатора. Виды катализа: положительный, отрицательный,

гомогенный и гетерогенный, ферментативный, аутокатализ – их краткая характеристика.

Ката́лиз (греч. κατάλυσις восходит к καταλύειν — разрушение) — избирательное ускорение одного из возможных термодинамически разрешенных направлений химической реакции под действием катализатора(ов), который многократно вступает в промежуточное химическое взаимодействие с участниками реакции и восстанавливает свой химический состав после каждого цикла промежуточных химических взаимодействий

По влиянию на скорость реакции катализ многие источники делят на положительный (скорость реакции растет) и отрицательный (скорость реакции падает). В последнем случае происходит процесс ингибирования, который нельзя считать 'отрицательным катализом', поскольку ингибитор в ходе реакции расходуется.

Катализ бывает гомогенным и гетерогенным (контактным). В гомогенном катализе катализатор состоит в той же фазе, что и реактивы реакции, в то время, как гетерогенные катализаторы отличаются фазой.

Гомогенный катализ

Примером гомогенного катализа является разложение пероксида водорода в присутствии ионов йода. Реакция протекает в две стадии:

H2О2 + I → H2О + IO

H2О2 + IO → H2О + О2 + I

При гомогенном катализе действие катализатора связано с тем, что он вступает во взаимодействие с реагирующими веществами с образованием промежуточных соединений, это приводит к снижению энергии активации.

Гетерогенный катализ

При гетерогенном катализе ускорение процесса обычно происходит на поверхности твердого тела — катализатора, поэтому активность катализатора зависит от величины и свойств его поверхности. На практике катализатор обычно наносят на твердый пористый носитель.

Механизм гетерогенного катализа сложнее, чем у гомогенного. Механизм гетерогенного катализа включает пять стадий, причем все они обратимы.

Диффузия реагирующих веществ к поверхности твердого вещества

Физическая адсорбция на активных центрах поверхности твердого вещества реагирующих молекул и затем хемосорбция их

Химическая реакция между реагирующими молекулами

Десорбция продуктов с поверхности катализатора

Диффузия продукта с поверхности катализатора в общий поток

Примером гетерогенного катализа является окисление SO2 в SO3 на катализаторе V2O5 при производстве серной кислоты (контактный метод).

ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ (биокатализ), ускорение биохим. р-ций при участии белковых макромолекул, называемых ферментами (энзимами). Ферментативный катализ- разновидность катализа, хотя термин "ферментация" (брожение)известен с давних времен, когда еще не было понятия хим. катализа.

Автокатализ — катализ химической реакции одним из её продуктов или исходных веществ. Одним из наиболее широко известных примеров автокатализа является окисление щавелевой кислоты перманганатом калия:

2MnO4− + 5C2O42− + 16H+ = 2Mn2+ + 10CO2 + 8H2O

Катализатором этой реакции являются ионы Mn2+. При комнатной температуре эта реакция вначале протекает медленно, но по мере накопления в растворе продукта-катализатора, она ускоряется.

Автокатализ играет ключевую роль в эволюционной химии, поскольку реакция, катализируемая собственными продуктами, получает преимущество перед реакциями, получающими катализатор извне (тем более - перед некаталитическими реакциями), что создает условия для естественного отбора.

• 57. Фазовые равновесия в гетерогенных системах. Правило фаз Гиббса. Понятия: фаза, степень

свободы, компонент, независимый компонент.

Большинство веществ могут существовать в одном из трех агрегатных состояний: газообразном (парообразном), жидком и твердом. В определенных условиях эти фазы способны переходить друг в друга, то есть всякую жидкость путем испарения можно перевести в газ, а охлаждением – в твердое состояние. На рис. 6.9 показаны взаимные фазовые превращения вещества.

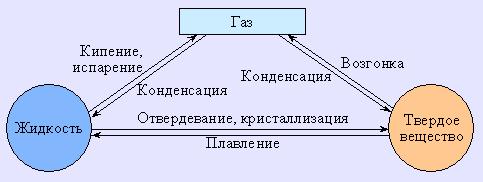
Рисунок 6.9

Взаимное превращение трех агрегатных состояний друг в друга

Равновесия между различными фазами одной системы называют фазовыми, а описывают эти фазовые равновесия посредством фазовых диаграмм или диаграмм состояния. Фазовая диаграмма позволяет установить условия равновесия между числом фаз, числом компонентов и числом степеней свободы (вариантностью) системы.

Фаза (Ф) – гомогенная (однородная по химическому составу и термодинамическим свойствам) часть системы, отделенная от других частей поверхностью раздела. Так, два нерастворимых друг в друге твердых вещества, как и две несмешивающиеся жидкости, образуют две фазы.

Компоненты (К) – химически индивидуальные вещества, наименьшее число которых достаточно для образования фаз системы.

Число компонентов определяется количеством индивидуальных веществ в системе за вычетом числа возможных между ними обратимых взаимодействий. Например, система из трех индивидуальных веществ H2O, H2, O2 будет двухкомпонентной, поскольку для образования всех фаз достаточно любых двух веществ:

= H2 + 1/2O2.

По числу компонентов системы делятся на одно-, двух-, трех- и многокомпонентные.

Степени свободы (С) – число параметров (температура, давление, состав системы), которые можно произвольно менять без изменения числа фаз в системе.

Правило фаз Гиббса: в изолированной равновесной системе число степеней свободы равно числу компонентов системы плюс два минус число фаз:

С = К + 2 – Ф

В качестве примера однокомпонентной системы, для которой правило фаз С = 3 – Ф, на рис. 6.10 приведена фазовая диаграмма диоксида углерода.

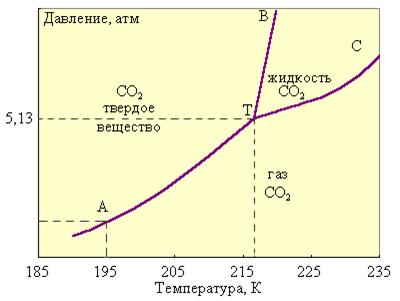
Рисунок 6.10

Фазовая диаграмма CO2

При P < 5,3 атм. CO2 в жидком состоянии не может находится. При атмосферном давлении твердый диоксид углерода сублимирует при 195 K.

Если один из параметров системы (температура или давление) имеет постоянное значение, то правило фаз принимает вид:

C = K + 1 – Ф.

Это уравнение используется при изучении конденсированных систем, состоящих только из твердых и жидких фаз, поскольку состояния равновесия в таких системах малочувствительны к изменению давления.

Наибольшее практическое значение имеют только изобарные диаграммы двухкомпонентных систем, содержащие только конденсированные фазы. Рассмотрим некоторые из них.

58. Однокомпонентные системы. Диаграмма состояния воды.

ОДНОКОМПОНЕНТНЫЕ СИСТЕМЫ

физ.-хим. системы, образованные одним компонентом. Состояние О. с. определяется двумя параметрами состояния. Число параметров состояния (вариантность О. с.), к-рое можно произвольно менять без изменения числа фаз, равно 2 для однофазной О. с., 1 - для двухфазной (напр., вода - пар) и нулю - для трёхфазной (напр., лёд - вода - пар).

Рассмотрим диаграмму состояния однокомпонентной системы на примере диаграммы состояния воды.

Области фазовой диаграммы, ограниченные кривыми, соответствуют тем условиям (температурам и давлениям), при которых устойчива только одна фаза вещества. Например, при любых значениях температуры и давления, которые соответствуют точкам диаграммы, ограниченным кривыми ВТ и ТС, вода существует в жидком состоянии. При любых температуре и давлении, соответствующих точкам диаграммы, которые расположены ниже кривых АТ и ТС, вода существует в парообразном состоянии.

Кривые фазовой диаграммы соответствуют условиям, при которых какие-либо две фазы находятся в равновесии друг с другом. Например, при температурах и давлениях, соответствующих точкам кривой ТС, вода и ее пар находятся в равновесии. Это и есть кривая давления пара воды. В точке Х на этой кривой жидкая вода и пар находятся в равновесии при температуре 373 К (100°С) и давлении 1 атм (101,325 кПа); точка Х представляет собой точку кипения воды при давлении 1 атм.

Кривая АТ является кривой давления пара льда; такую кривую обычно называют кривой сублимации.

Кривая ВТ представляет собой кривую плавления. Она показывает, как давление влияет на температуру плавления льда: если давление возрастает, температура плавления немного уменьшается. Такая зависимость температуры плавления от давления встречается редко. Обычно возрастание давления благоприятствует образованию твердого вещества. В случае воды повышение давления приводит к разрушению водородных связей, которые в кристалле льда связывают между собой молекулы воды, заставляя их образовывать громоздкую структуру. В результате разрушения водородных связей происходит образование более плотной жидкой фазы.

В точке Y на кривой ВТ лед находится в равновесии с водой при температуре 273 К (0°С) и давлении 1 атм. Она представляет собой точку замерзания воды при давлении 1 атм.

Кривая SТ указывает давление пара воды при температурах ниже ее точки замерзания. Поскольку вода в нормальных условиях не существует в виде жидкости при температурах ниже ее точки замерзания, каждая точка на этой кривой соответствует воде, находящейся в метастабильном состоянии. Это означает, что при соответствующих температуре и давлении вода находится не в своем наиболее устойчивом (стабильном) состоянии. Явление, которое соответствует существованию воды в метастабильном состоянии, описываемом точками этой кривой, называется переохлаждением.

На фазовой диаграмме имеются две точки, представляющие особый интерес. Прежде всего, отметим, что кривая давления пара воды заканчивается точкой С. Она называется критической точкой воды. При температурах и давлениях выше этой точки пары воды не могут быть превращены в жидкую воду никаким повышением давления. Другими словами, выше этой точки паровая и жидкая формы воды перестают быть различимыми. Критическая температура воды равна 647 К, а критическое давление составляет 220 атм.

Точка Т фазовой диаграммы называется тройной точкой. В этой точке лед, жидкая вода и пары воды находятся в равновесии друг с другом. Этой точке соответствуют температура 273,16 К и давление 6,03 10-3 атм. Лишь при указанных значениях температуры и давления все три фазы воды могут существовать вместе, находясь в равновесии друг с другом.

59. Термический анализ состояния двухкомпонентных систем. Диаграммы плавкости, их типы.

Диаграмма состояния представляет собой графическое изображение фазового состояния сплавов и критических точек в зависимости от температуры и концентрации в условиях равновесия.

Для того чтобы обеспечить равновесное состояние системы, охлаждение сплава из жидкого состояния осуществляют очень медленно. Равновесными считаются такие условия, при которых процессы, протекающие в системе, являются обратимыми. В данном случае – процессы, происходящие при охлаждении сплава, должны в точности совпадать с процессами, протекающими при его нагреве.

Диаграмму состояния строят в координатах температура – концентрация (рис. 3.4). Для сплавов, состоящих из двух компонентов А и В, состав характеризуется отрезком прямой, принятым за 100 %. Крайние точки А и В соответствуют 100 % чистых компонентов. Любая точка на этом отрезке характеризует состав двойного сплава. Так, например, точка С соответствует сплаву, состоящему из 20 % В и 80 % А; точка D – 60 % В и 40 % А.

Для построения диаграммы состояния из компонентов изготовляют серию сплавов различного состава и для каждого из них строят кривую охлаждения по результатам термического анализа в координатах температура – время (так же, как для металлов). Особенности поликристаллического строения сплавов в твердом состоянии изучаются с помощью оптического микроскопа обычно при 100–1000-кратном увеличении. Атомная структура сплавов и параметры кристаллических решеток определяются методом рентгеноструктурного анализа.

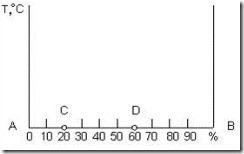
Рис. 3.4. Координаты для изображения диаграммы состояния двухкомпонентной системы

В зависимости от характера строения двухкомпонентных сплавов (в жидком состоянии оба компонента неограниченно растворяются друг в друге, образуя однородный жидкий раствор) различают следующие основные типы диаграмм состояния:

1) при образовании компонентами механической смеси;

2) при неограниченной растворимости компонентов в твердом состоянии;

3) при ограниченной растворимости компонентов в твердом состоянии;

4) при образовании компонентами химического соединения.

Диаграмма состояния сплавов из компонентов,

образующих в твердом состоянии механическую смесь

Экспериментально установлено, что при совместной кристаллизации сплавов, компоненты которых не растворяются друг в друге в твердом состоянии, температура начала кристаллизации всегда ниже, чем у исходных компонентов. Температура же окончания процесса перехода в твердое состояние одинакова для сплавов любого состава двухкомпонентной системы.

• 60. Диаграммы состояния систем с эвтектикой, химическим соединением, твердыми растворами. Правило рычага.

На рис. 3.5 приведена диаграмма состояния сплава с компонентами А и В. Выше линии КСN все сплавы двухкомпонентной системы представляют собой однофазный жидкий сплав (ж. с.). Эта линия называется линией ликвидуса (с греч. – жидкий), линия DСЕ – линией солидуса (с греч. – твердый). Ниже линии DСЕ все сплавы находятся в твердом состоянии. Сплав, соответствующий точке С, называется эвтектическим (эвтектикой).

Эвтектикой, таким образом, называется механическая смесь кристаллов двух (или более) твердых веществ, одновременно закристаллизовавшихся из жидкого сплава при температуре ниже температуры плавления отдельных компонентов или любых других их смесей. Это определение относится к твердой эвтектике. Жидкой эвтектикой называется жидкий расплав (раствор), из которого возможна такая кристаллизация.

В отличие от эвтектики, эвтектоид – аналогичная ей составляющая металлических сплавов, – образуется не из жидкой, а из твердой фазы. Эвтектоид, по сравнению с эвтектикой, имеет более тонкое дисперсное строение из двух или более фаз.

Рис. 3.5. Диаграмма состояния сплавов, образующих в твердом состоянии механическую смесь компонентов А и В

Эвтектический сплав данной системы имеет строго определенное процентное соотношение компонентов А и В. Сплавы, расположенные слева от эвтектики, называются доэвтектическими, а справа – заэвтектическими.

В доэвтектических сплавах сначала при охлаждении ниже линии ликвидуса КС выделяются кристаллы компонента А, а в заэвтектических – ниже линии СN – кристаллы компонента В.

После затвердевания, т.е. ниже линии солидуса DСЕ, доэвтектические сплавы состоят из кристаллов А и эвтектики, а заэвтектические – из кристаллов В и эвтектики.

Дисперсные системы – системы, где одно вещество в виде частиц

различной величины распределено в другом веществе.

Степень раздробленности вещества называется степенью дисперсности

Д=1/d (величина обратная среднему диаметру частицы).

Среда, в которой находится диспергированное (раздробленное) вещество

называется дисперсионной средой, а раздробленное вещество в виде частиц

разных размеров - дисперсной фазой.

Дисперсионная среда и дисперсная фаза - это дисперсная система.

Классификация дисперсных систем:

1. По степени дисперсности:

1) Грубодисперсные - размер частиц - 10−7

- 10−5 м;