МАТЕМАТИКА
ИРЭ (ЭТФ), Эр–1  7, Эл-15, 2 семестр, 23, 2016/2017 уч. год
7, Эл-15, 2 семестр, 23, 2016/2017 уч. год
Лектор: доц. Ратникова Т.А.
Экзаменационная программа
1. Несобственные интегралы с неограниченным верхним пределом от неотрицательных функций. Теоремы сравнения.
2. Свойства несобственных интегралов с бесконечным верхним пределом (линейность, интегрирование по частям, формула Ньютона-Лейбница).
3. Приложения определенного интеграла. Вычисление площади фигуры, длины дуги, объема тел вращения.
4. Обыкновенные дифференциальные уравнения. Решение дифференциального уравнения. Общее и частное решение. Формулировка теоремы о существовании и единственности решения задачи Коши для дифференциального уравнения первого порядка.
5. Уравнения с разделяющимися переменными, линейные уравнения первого порядка. Метод вариации произвольной постоянной. Метод Бернулли.
6. Однородные уравнения. Уравнения Бернулли.
7. Дифференциальные уравнения, допускающие понижение порядка.
8. Линейные однородные дифференциальные уравнения n -го порядка с постоянными коэффициентами. Фундаментальная система решений.
9. Линейные неоднородные дифференциальные уравнения n -го (n>1) порядка с постоянными коэффициентами. Теорема о структуре решения. Метод подбора частного решения.
10. Линейные неоднородные дифференциальные уравнения n -го (n>1) порядка с постоянными коэффициентами. Метод вариации постоянных.
11. Множества в n-мерном пространстве. ФНП. Линии и поверхности уровня.
12. Частные производные первого порядка, геометрический смысл.
13. Дифференцируемость функций многих переменных. Необходимое условие дифференцируемости. Полный дифференциал. Достаточные условия дифференцируемости функции многих переменных.
14. Касательная плоскость и нормаль к поверхности.
15. Достаточные условия экстремума функции двух переменных.
16. Условный экстремум. Функция Лагранжа. Необходимое условие условного экстремума. Достаточные условия условного минимума (максимума).
17. Неявные функции. Теорема о разрешимости неявной функции. Производная функции, заданной неявно.
18. Дифференцирование сложной функции многих переменных. Инвариантность формы первого дифференциала для функций многих переменных.
19. Скалярное поле. Примеры. Градиент скалярного поля, производная по направлению и ее связь с градиентом. Свойства градиента скалярного поля.
20. Формула Тейлора для функций многих переменных.
21. Числовая последовательность. Предел числовой последовательности, его свойства. Арифметические действия с последовательностями, имеющими предел. Ограниченность последовательности, имеющей предел. Существование предела у ограниченной монотонной последовательности.
22. Числовой ряд. Сумма и сходимость ряда. Остаток ряда. Арифметические операции с рядами. Необходимый признак сходимости. Ряды с положительными членами. Признаки сравнения.
23. Достаточные признаки сходимости рядов с положительными членами: признаки Даламбера, Коши; интегральный признак Коши.
24. Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость. Теорема Лейбница. Оценка остатка условно сходящегося ряда. Действия с абсолютно сходящимися рядами.
25. Функциональный ряд. Область сходимости. Признак Вейерштрасса.
26. Степенные ряды. Теорема Абеля. Интервал сходимости. Непрерывность суммы степенного ряда. Интегрирование и дифференцирование степенного ряда (без доказательства).
27. Ряд Тейлора. Разложение функции в ряд Тейлора. Теорема о разложении в ряд Тейлора.
28. Единственность разложения в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора. Применение степенных рядов.
29. Тригонометрическая система функций. Тригонометрический ряд Фурье, условия его сходимости и свойства суммы.
30. Тригонометрические ряды Фурье для четных и нечетных функций, их свойства. Ряды Фурье по косинусам и синусам, условия их сходимости и свойства суммы.
Перечень задач к экзамену:
1. Найти площадь фигуры, ограниченной данными кривыми:
а) 
б) 
2. Исследовать на сходимость ряд: 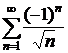 ;
;  .
.
3.Найти область сходимости ряда:  .
.
4.Вычислить с точностью 0,01: 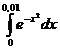 .
.
5.Разложить функцию 
а) в ряд Фурье по косинусам на интервале  ;
;
б) в ряд Фурье на интервале  и построить график суммы ряда
и построить график суммы ряда  :
: 
6. Разложить в ряд Тейлора по степеням x:  .
.
7.Найти локальный экстремум функции и составить уравнения касательной плоскости и нормали в точке экстремума

8.Составить уравнение касательной плоскости в точке 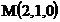 и вычислить градиент и производную по направлению к поверхности уровня функции
и вычислить градиент и производную по направлению к поверхности уровня функции 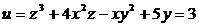 в направлении вектора
в направлении вектора  .
.
9. Решить уравнения:
1. Найти общее решение или общий интеграл дифференциального уравнения и сделать проверку: 
2. Решить задачу Коши и сделать проверку: 
3. Найти общее решение уравнения и сделать проверку:
а)  ; б)
; б)  ; в)
; в)  .
.
 2018-01-08
2018-01-08 1072
1072






