Глава 4. Основы моделирования в медицине

4.1. ПОНЯТИЕ МОДЕЛИ

Моделирование - это метод познания, состоящий в создании и исследовании моделей. Модель - это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Таким образом, в понятие «модель» обычно вкладывается общий смысл сходства, подобия образца, какого-то отражения, т. е. наличие внешнего, чувственно-наглядного, осязаемого и зримого сходства оригинала с копией. Кроме факта соответствия важен и критерий этого соответствия: чему именно в отражаемом явлении должна соответствовать модель. Таким образом, давая представление о моделировании, следует отметить такие важные свойства модели, как, вопервых, соответствие свойств модели свойствам предмета и, во-вторых, определенный критерий этого соответствия.

При изучении различных сторон сложных объектов приходится упрощать модель, отказываясь от отражения некоторых ее свойств. Поэтому модель, в некотором смысле, проще реального объекта, поскольку не охватывает все стороны моделируемого оригинала. В первую очередь это связано со сложностью оригинала, к которому относятся живые системы. В дальнейшем, по мере расширения знаний, модель может дополняться различными деталями, все ближе и ближе приближаясь к реальному объекту. Поэтому построение модели носит циклический характер, направленный на постепенное приближение модели к оригиналу. По известному выражению одного из пионеров кибернетики У.Р. Эшби: «Лучшая модель кошки - сама кошка».

Однако модель - это не только отражение наших знаний об исследуемом объекте, но и источник новых сведений, полученных с помощью модели. Исследование модели позволяет оценить поведение моделируемого объекта в новых условиях или при различных воздействиях, которые на реальном объекте проверить невозможно (исследование на людях) или затруднительно (дорогостоящие объекты или негативные последствия экспериментов).

 

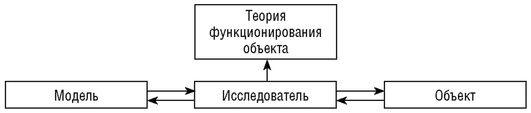
Рис. 4.1. Процесс моделирования

Поэтому в более широком смысле модель можно рассматривать как мысленно представляемую или материально реализованную систему, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает новую информацию об этом объекте.

Процесс моделирования включает три элемента: субъект (исследователь), объект исследования и модель, опосредующую отношения познающего субъекта и познаваемого объекта (рис. 4.1). Сравнивая результаты модельных экспериментов и функционирование реального объекта, а также их реакции на изменяющиеся условия, возможно перенести знания, полученные при изучении модели, на объект. Таким образом, знания, полученные при исследовании модели и дополненные свойствами оригинала, которые не нашли отражение в модели, могут быть использованы для получения теории функционирования объекта (см. рис. 4.1).

4.2. КЛАССИФИКАЦИЯ МОДЕЛЕЙ

Существует множество классификаций, поскольку сам процесс познания окружающей действительности состоит в непрерывном моделировании наблюдаемых явлений. Рассмотрим некоторые из них.

4.2.1. Классификация моделей по методологии применения

Учебные модели воспроизводят функциональные особенности объекта или его структуру, что дает возможность учащимся изучить свойства оригинала, которые невозможно наблюдать на живом объекте. К ним относятся модели клетки, сердечно-сосудистой системы, различные тренажеры, макеты отдельных органов и опорно-двигательного аппарата.

Опытные модели используются для исследования объекта и прогнозирования его будущих характеристик. Например, искусственные протезы клапанов сердца.

 

Научно-исследовательские модели создаются для исследования процессов и явлений. К ним относятся модели распространения инфекционных заболеваний, кинетики лекарственных веществ в организме, модель камер сердца и его клапанов.

Игровые модели - это различного рода игры: деловые, экономические, лечебные. С помощью таких моделей можно разрешать конфликтные ситуации, оказывать психологическую помощь, проигрывать поведение объекта в различных ситуациях.

Имитационные модели имитируют реальность с той или иной степенью точности.

4.2.2. Классификация моделей в зависимости от целей использования

Оптимизационные модели предназначены для определения новых свойств моделируемого объекта. Пример - расчет вероятности развития осложнения после операции.

Описательные модели описывают поведение некоторой системы и не предназначены для целей управления. Это, например, формулы, описывающие изменение концентрации лекарственного вещества в крови после его введения.

4.2.3. Классификация моделей по способу представления

Предметные модели воспроизводят геометрические, физические и другие свойства объектов в материальном мире. Например, искусственный хрусталик, искусственный тазобедренный сустав, скелет человека.

Информационные модели отражают свойства объектов, предметов или процессов с помощью ассоциативных знаков (слова, рисунки, схемы, чертежи, формулы и т. д.). Например, схема кровоснабжения сердца.

Типы информационных моделей: словесные, графические, математические.

В зависимости от структуры информационные модели делятся на табличные, иерархические и сетевые.

4.2.4. Классификация моделей в зависимости от временного фактора

Статические модели описывают систему в определенный момент времени. Например, классификация заболеваний, методов исследования.

Динамические модели описывают процессы изменения и развития систем. Пример - схематическое описание развития физиологических систем в процессе развития ребенка.

 

4.2.5. Классификация моделей, применяемых в медицине

Вещественные (структурные) модели воспроизводят структуру объекта и взаимоотношение его частей. Примером таких моделей в медицине могут служить различные протезы, по внешнему виду похожие на реальные части тела, которые они замещают. В технике к вещественным моделям относят уменьшенные копии самолетов, плотин, зданий, которые используются для оценки некоторых характеристик этих объектов в экспериментальных условиях.

Энергетические (функциональные) модели используются для моделирования функциональных взаимоотношений в изучаемых объектах. Эти модели по внешнему виду не напоминают моделируемые объекты, но их целью является выполнение функций этих объектов. Например, в медицине широко используются такие системы, как аппарат искусственной почки или искусственного дыхания.

Структурно-функциональные модели сочетают свойства вещественных и энергетических моделей, т. е. и по внешнему виду, и по выполняемым функциям модели подобны заменяемым органам. К таким моделям относятся биоуправляемые протезы, искусственный хрусталик глаза, последние разработки в области искусственного сердца.

В отличие от первых двух моделей информационные модели производят описание объекта. В медико-биологических исследованиях до недавнего времени для описания работы биологических систем использовали преимущественно словесные модели. Однако с помощью словесных моделей затруднительно четко изложить закономерности работы изучаемого объекта. Поэтому все чаще применяются математические модели, которые используют количественные соотношения между параметрами исследуемой биосистемы.

 

Математическая модель представляет собой систему математических соотношений - формул, функций, уравнений, систем уравнений и т. п., описывающих те или иные стороны изучаемого объекта, явления, процесса. Использование математических моделей позволяет перейти к сжатому изложению гипотез и закономерностей, а главное - к широкому применению компьютерных технологий.

Кроме рассмотренных классов моделей в медицине широко распространены биологические модели. Для изучения протекания патологических процессов, отработки новых методов хирургического вмешательства и изучения новых лекарственных средств широко используют биологические модели различных животных. Полученные результаты с определенной долей осторожности переносятся на человека. В зависимости от целей исследования подбирают животных так, чтобы уровень организации изучаемой системы был близок к уровню организации таковой у человека. Например, биологической моделью наследственной артериальной гипертензии человека являются спонтанно гипертензивные крысы, выведенные Окамото и Аоки (1967) из популяции крыс линии Вистар-Киото. У спонтанно гипертензивных животных артериальное давление спонтанно повышается с 4-5-й недели жизни ввиду реализации наследственных механизмов. Причем стадии развития болезни и ее осложнения аналогичные, как и при наследственной артериальной гипертензии человека.

4.3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В МЕДИЦИНЕ

Наибольшее значение в медицинских исследованиях получили математические модели. Обычно это система уравнений, описывающая взаимосвязь между переменными, характеризующими реальный физиологический процесс или систему. Математические модели подразделяются на детерминированные и вероятностные. В детерминированных моделях переменные и параметры предполагаются постоянными или описываются детерминированными функциями. В вероятностных моделях характеризующие ее переменные и параметры являются случайными функциями или случайными величинами.

 

Детерминированные математические модели чаще всего представляют собой систему алгебраических или дифференциальных уравнений. Вероятностные модели строятся по результатам экспериментального определения статических или динамических характеристик объектов на основе методов математической статистики.

Необходимость применения в медицине математических методов моделирования с использованием компьютерной техники диктуется тем, что с их помощью можно адекватно и в короткий срок обобщить сложную сущность явлений и процессов, описать и понять факты, выявить взаимосвязи, найти рациональное решение с гораздо большей полнотой и надежностью, чем это делается на базе словесных характеристик; элементарных рутинных расчетов.

В настоящий момент времени сформировалось представление о том, что может дать применение метода математического моделирования в медицине:

• систематизировать и объединять знания о физиологических системах;

• идентифицировать важные параметры (физиологически содержательные свойства) и определять общую чувствительность системы к вариации каждого параметра;

• количественно оценивать трудноизмеряемые и вообще неизмеряемые показатели;

• быстро и эффективно проверять гипотезы без обращения к эксперименту;

• планировать эксперименты и исследования;

• предсказывать поведение реальной системы.

Успех математического моделирования в медицине зависит от того, насколько глубоко исследованы системы организма и на этой основе эффективно выделены информативные подпространства признаков. Авторы моделей в математическом описании функций организма отражают физические, биохимические, физиологические и структурные характеристики объекта исследования.

Важной проблемой в математическом моделировании в медицине является адекватность математического выражения биологического явления. Проблемность этой ситуации состоит в том, что математический аппарат создавался в расчете на изучение процессов неживой природы (механических, атомных, молекулярных), характеризующихся одномерным распределением, которое не свойственно биопроцессам.

 

Живые системы обладают целым рядом специфических характеристик, отличающих их от неживых систем. Основные особенности живых систем заключаются в следующем.

1. Биологические системы являются открытыми системами, обменивающимися с окружающей средой веществом, энергией и информацией.

2. Живые объекты относятся к сложным системам, имеющим пространственное структурирование, многокомпонентность и вероятностный характер поведения.

3. Биологические объекты относятся к размножающимся системам, т. е. способным к авторепродукции.

4. В биологических системах имеется сложная иерархическая система регулирования. Регуляция процессов жизнедеятельности происходит на клеточном, органном, системном уровнях и на уровне целостного организма. Все эти уровни взаимосвязаны между собой и обмениваются информацией для выработки оптимальных управляющих сигналов.

4.3.1. Этапы построения математической модели

Построение математических моделей биосистем подразумевает проведение экспериментальных исследований для получения количественных характеристик изучаемых процессов. В дальнейшем эти характеристики становятся объектом исследования, и на их основе с учетом теоретических предпосылок строится модель, объясняющая функционирование изучаемого объекта. Наивысшей точкой такого обобщения является математическая модель, заменяющая реальный объект исследования. Построенная модель представляет собой некоторое упрощение реального объекта как по структуре, так и по сложности внутренних и внешних связей, но обязательно отражает те свойства объекта, которые являются целью исследования.

 

В дальнейшем модель подвергается всесторонней проверке и корректировке для более полного соответствия модели и реального объекта. Н.М. Амосов предложил следующие этапы построения математических моделей живых систем.

1. Постановка задачи, которая заключается в определении цели исследования и моделирования на основании некоторой первоначальной гипотезы.

2. Построение функциональной схемы объекта - определение входов и выходов, режимов изменения входных воздействий, исследуемых режимов (норма, патология).

3. Планирование эксперимента. На этом этапе определяют режимы изменения входных сигналов, внутренних состояний системы, производится отработка комплекса контрольно-измерительной аппаратуры.

4. Проведение серии пробных опытов для отработки методики исследований, приемлемости принятых допущений, проверки исходной гипотезы.

5. Проведение основной серии опытов для получения статических и динамических характеристик.

6. Предварительная статистическая обработка материала, полученного на стадии экспериментирования с биосистемой.

7. Выбор типа и вида модели на основании анализа результатов статистической обработки данных.

8. Определение параметров модели по результатам экспериментов.

9. Всестороннее исследование математической модели биосистемы с целью определения достоверности и границ применимости модели.

Сравнение результатов, полученных с помощью модели и реального объекта, позволяет определить основные показатели качества модели:

• информативность, которая оценивается корреляцией между экспериментальным значением отклика системы на внешнее воздействие и значением отклика, рассчитанным по модели;

• адекватность, которая означает отражение моделью с заданной точностью определенной совокупности свойств объекта;

• устойчивость коэффициентов регрессии и структуры модели.

Статические модели сердечно-сосудистой системы позволяют получить и исследовать аналитические выражения, связывающие переменные кровообращения с параметрами, характеризующими насосную функцию сердца и резистивно-емкостные свойства сосудистого русла.

 

Ряд моделей статики сердечно-сосудистой системы, разработанных В.А. Лищуком, использовались в эксперименте и клинике сердечнососудистой хирургии. Особенностью этих исследований является то, что в каждом конкретном случае выбирается модель, все параметры которой могут быть определены на основании измеряемых переменных. Используя показатели, измеряемые и вычисляемые по модели, осуществляется процедура идентификации с целью перехода от модели, описывающей общие для некоторого класса больных свойства и отношения, к индивидуальной модели сердечно-сосудистой системы больного, в данный момент находящегося под наблюдением. Эта модель применяется для выбора лечения в реальном времени, причем с такой целью и таким образом, чтобы объединить:

• физиологические знания;

• клинический опыт;

• текущие наблюдения;

• возможности математических методов;

• возможности вычислительной и измерительной техники;

• искусство врача.

Направленность на клиническое применение определила особые требования к математическим моделям: необходимость отражения патологических процессов и компенсаторных сдвигов, лечебных воздействий (медикаментозных, изменения режима вентиляции, жидкостного баланса и пр.), представления клинического контроля, оценку модели в реальном времени, а также наличие интерактивного (диалогового) интерфейса (общения) в терминах, принятых в клинике.

Например, создание математических моделей сердечно-сосудистой системы имеет следующее практическое применение:

• возможность управления вспомогательным кровообращением и контрпульсацией;

• разработка индексов, оценивающих состояние сердечной деятельности, для постановки диагноза;

• исследование зон локализации инфаркта и их влияние на гемодинамику;

• определение параметров аорты и сердечного выброса.

 

Наиболее приемлемой клинической базой, где активно внедряются методы математического моделирования сердечно-сосудистой системы, стала реанимация и интенсивная терапия. Например, моделирование пороков сердца является в настоящее время одним из развивающихся направлений. В моделях пороков сердца могут быть заданы изменения связей (например, увеличение сопротивления или регургитация при стенозах), введение новых связей (дефекты межпредсердных и межжелудочковых перегородок), учет новых связей (аневризма). Самостоятельным направлением является разработка математических моделей хронических форм сердечной недостаточности. При сердечной недостаточности выводят, например, зависимость сердечного выброса от уровня артериального давления, оценивают роль правых отделов сердца в развитии острой сердечной недостаточности. Развитие трансплантологии привело к развитию многочисленных модельных исследований систем управления искусственным сердцем. Кроме того, получены новые знания о влиянии сильнодействующих лекарств кардиотонического и вазоплегического действия на сердечно-сосудистую систему, их фармакодинамике и фармакокинетике. Математические модели сердечно-сосудистой системы, позволяющие выявить причины перегрузки сердца сразу после проведенных на нем операций, являются неотъемлемой частью таких методов измерения, как доплеровское зондирование, ядерный магнитный резонанс.

4.3.2. Примеры математических моделей Модель динамики популяции

Изменение численности популяции весьма важно для прогнозирования скорости размножения особей одного вида, проживающих на конкретной территории или в определенном ограниченном объеме. Это связано с распространением вирусов, сообществ животных, а также с ростом численности населения Земли. Именно первая математическая модель, предложенная священником Томасом Мальтусом в 1778 г., так и называлась - «Трактат о народонаселении». Модель, предложенная Мальтусом, описывала изменение численности народонаселения Земли, но она может применяться для описания изменения популяции и других живых организмов.

 

В данной математической модели рассматриваются изменения численности популяции при условии отсутствия внешних пагубных факторов, сдерживающих увеличение численности. Таким образом, в качестве упрощения вводятся следующие допущения.

1. В пространстве проживания популяции отсутствуют вредные воздействия, приводящие к снижению численности популяции.

2. Скорость прироста популяции прямо пропорциональна количеству особей популяции.

Пусть численность популяции в момент времени t равна x(t). Прирост численности популяции определяется разностью между количеством родившихся и умерших особей (е).

Тогда

или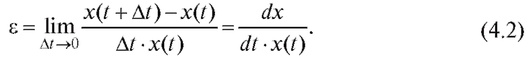

Решаем дифференциальное уравнение (4.2) при начальном условии x(0) = x₀, где x₀ - начальная численность популяции. Получаем: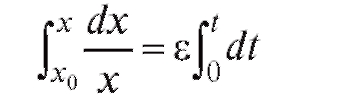

или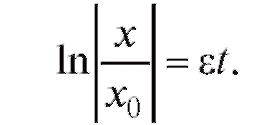

Тогда имеем

Согласно полученному решению численность популяции будет определяться приростом популяции (ε). Если количество родившихся особей будет больше умерших, то будет экспоненциальный рост численности населения. При отрицательном приросте (ε < 1) численность популяции будет стремиться к нулю (рис. 4.2).

В реальных условиях всегда есть сдерживающие факторы, которые влияют на прирост популяции (конкуренция между особями, ограниченность пищи, стихийные бедствия, болезни и т. п.). Поэтому в 1845 г. П.Ф. Ферхюльст дополнил модель Мальтуса ограничениями на рост популяции. Ограничение заключалось в том, что любая популяция может достигать только определенного максимума x_max и коэффициент прироста е должен снижаться при достижении этого значения. Введем относительную величину численности популяции:

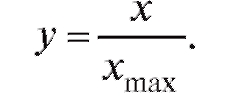
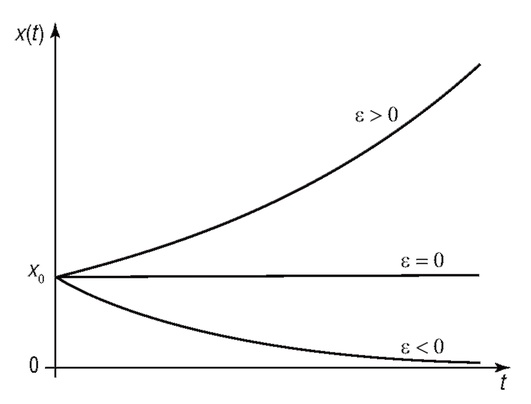
Рис. 4.2. Изменение численности популяции при отсутствии сдерживающих факторов

Тогда в модели Ферхюльста относительный прирост численности популяции будет равен: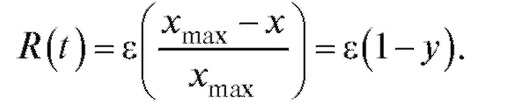

Подставляя в уравнение (4.2), получим:

 

Решая данное дифференциальное уравнение при начальных условиях y(0) = y₀ методом разделения переменных, получим:

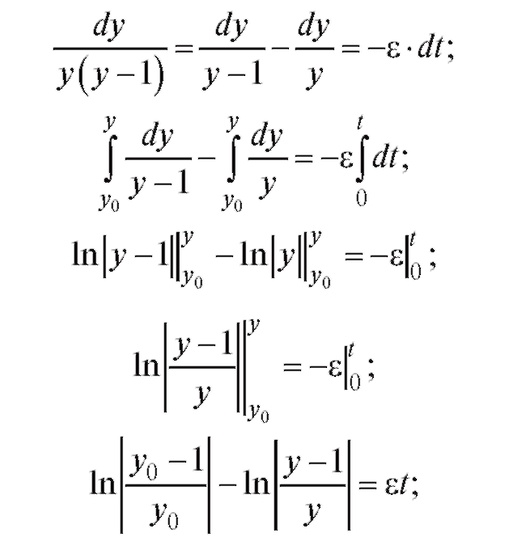
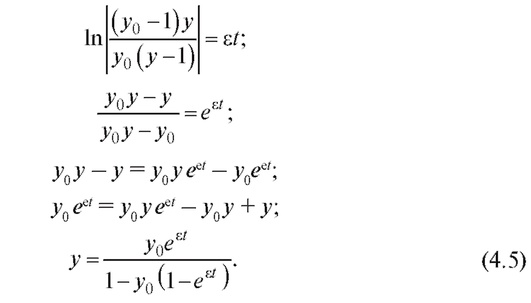
На рис. 4.3 показаны графики изменения относительной численности популяции при различных значениях y₀ и ε (при условии, что ε > 0, т. е. рождаемость особей превышает их смертность). В этом случае численность популяции приближается к x_max с различной скоростью в зависимости от величины е.

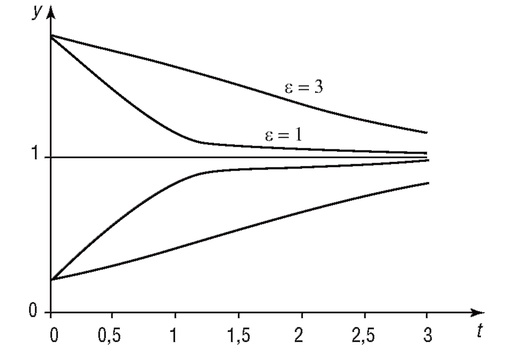
Рис. 4.3. Изменение относительной численности популяции (ε = 1 и 3; y₀ = 0,2 и 1,8)

Модель сосудистого русла

Первой упрощенной моделью сосудистой системы, позволяющей рассчитать изменение давления в некоторой точке крупного сосуда (аорте), была модель упругого резервуара, предложенная в 1899 г. немецким физиологом Отто Франком. В этой модели артериальная часть большого круга кровообращения представлена упругой камерой, а система периферических мелких сосудов моделируется жесткой трубкой (рис. 4.4).

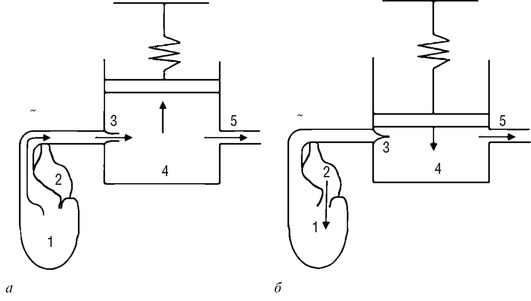
Рис. 4.4. Гидродинамическая модель упругого резервуара сосудистого русла в фазы систолы и диастолы: а -1-я фаза, аортальный клапан открыт; б - 2-я фаза, аортальный клапан закрыт

На рис. 4.4 показано схематическое изображение кровотока в аорте и мелких сосудах при сокращении и расслаблении сердечной мышцы. В фазу выброса (см. рис. 4.4, а) крови из левого желудочка сердца (1) кровь через аортальный клапан (3) поступает в аорту (4) и увеличивает ее объем благодаря упругим свойствам стенок аорты. Поэтому часть крови резервируется в аорте вследствие увеличения ее объема, а часть поступает в мелкие сосуды (5). В фазу диастолы (см. рис. 4.4, б) аортальный клапан (3) закрывается, и благодаря упругим свойствам стенок аорты ее объем возвращается к исходным размерам и происходит изгнание крови в мелкие сосуды (5). В эту фазу кровь из левого предсердия (2) поступает в левый желудочек сердца (1). Данная модель весьма упрощенно рассматривает процессы, связанные с сокращением сердечной мышцы и выбросом ударного объема крови. Предполагается, что только крупные сосуды обладают свойством эластичности C, а мелкие сосуды представляют собой жесткую трубку (C ≈ 0). Кроме того, гидравлическое сопротивление крупных сосудов предполагается минимальным (R ≈ 0), а сопротивление мелких сосудов (артериол и капилляров) велико.

 

Реальные изменения давления и скорости сердечного выброса изображены на рис. 4.5.

Несмотря на значительные упрощения, данная модель позволяет описать зависимость между объемной скоростью кровотока Q с давлением в аорте P, периферическим сопротивлением мелких сосудов Я и эластичностью крупных сосудов C.

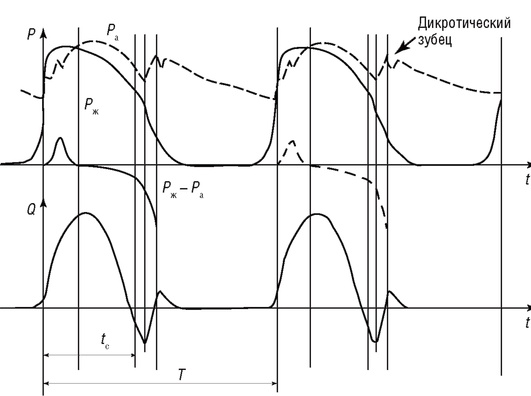
Рис. 4.5. Изменение давления P и скорости сердечного выброса Q в течение сердечного цикла (Р_а - давление в аорте; Р_ж - давление в желудочке)

Составим уравнения, описывающие эти процессы.

Объем крови в аорте (V) в систолу будет определяться величиной «ненаполненного» объема аорты (т. е. при P = 0) и величиной давления в фазу систолы.

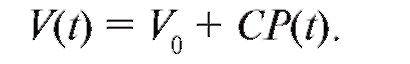(4.6)

Зная объем крови, можно рассчитать объемную скорость кровотока как изменение объема в единицу времени, т. е.

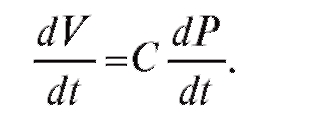(4.7)

Тогда, согласно закону сохранения объема несжимаемой жидкости, можно записать:

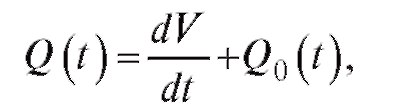(4.8)

где Q(t) - объемная скорость кровотока из левого желудочка сердца; Q₀(t) - объемная скорость кровотока, вытекающая из крупных сосудов.

На основании уравнения Пуазейля можно записать:

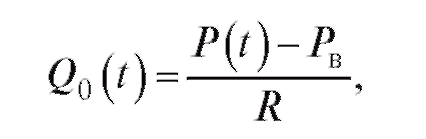(4.9)

где P - давление в крупных сосудах; Р_в - венозное давление, которое можно принять равным нулю. Тогда

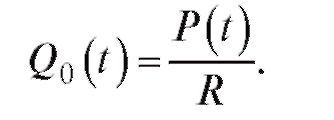(4.10)

Подставляя формулу (4.10) в (4.8), получим

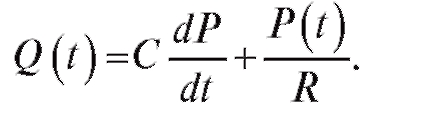(4.11)

Простое решение этого уравнения имеется для второй фазы сокращения сердца, т. е. когда закрывается аортальный клапан и Q(t) = 0. Тогда уравнение (4.11) имеет вид:

(4.12) 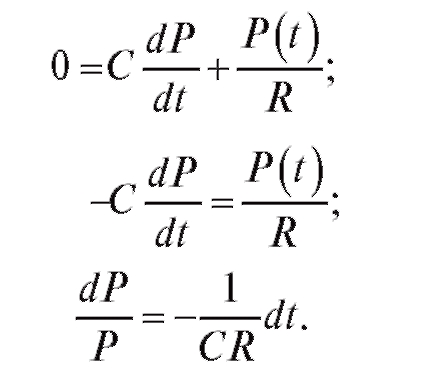(4.13)

Проинтегрируем формулу (4.13), с учетом того, что при t = 0 давление равно P₀ - давлению в крупных сосудах при закрытии аортального клапана (близко к систолическому давлению).

(4.14) 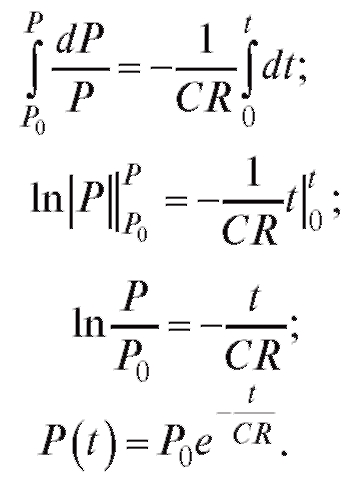(4.15)

На рис. 4.6 приведено решение дифференциального уравнения (4.12), которое описывает изменение давления в аорте и крупных сосудах в фазу диастолы (сплошная линия). Сравнение данного графика с реальной кривой (см. рис. 4.5), отражающей изменение давления в аорте после закрытия аортального клапана, показывает их подобие. Однако в этой фазе модель не отражает наличие дикротического зубца, имеющего место в реальной системе и связанного с небольшим увеличением давления после окончания систолы. Дикротический зубец отражает кратковременный обратный ток в аорте после закрытия аортального клапана.

 

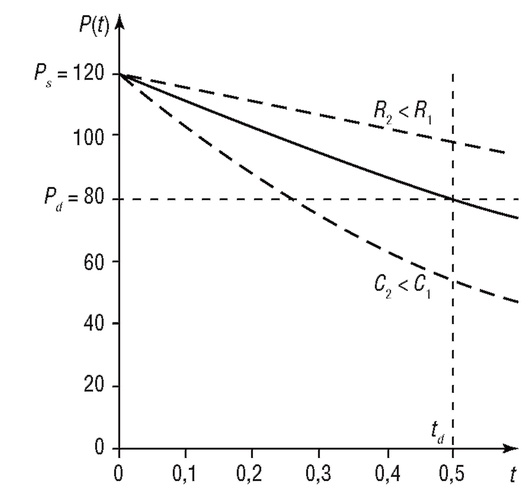
Рис. 4.6. Изменение давления крови в аорте и крупных сосудах после закрытия аортального клапана

Исследуя данную математическую модель, возможно изучить зависимость давления в крупных сосудах в фазе диастолы от величины эластичности сосудов C и гидравлического сопротивления сосудов Я (см. рис. 4.6, пунктирные линии).

Уравнение (4.11) является неоднородным линейным дифференциальным уравнением, и его решение зависит от вида функции Q(t). Аппроксимируя Q(t) полусинусоидальной или параболической функцией, можно получить решение, описывающее изменение давления в 1-ю фазу сокращения сердца.

На основе гидромеханической модели может быть построена электрическая модель гемодинамических процессов в сосудистой системе (рис. 4.7, а).

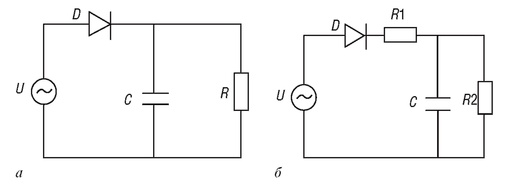
Рис. 4.7. Электрическая модель гемодинамики сосудистого русла: а - электрическая модель системной гемодинамики; б - электрическая модель системной гемодинамики с учетом сопротивления аорты

Насосную функцию сердца в этой модели представляет источник переменного сигнала U, диод D осуществляет роль сердечного клапана и пропускает только полуволну сигнала, тем самым моделирует выброс крови из левого желудочка сердца в фазу систолы, конденсатор C накапливает заряд в течение этого полупериода и отражает упругие свойства крупных сосудов, а сопротивление Я характеризует гидравлическое сопротивление мелких сосудов. Наличие конденсатора в этой цепи приводит к сглаживанию импульсных колебаний давления крови. Таким образом, напряжение на входе электрической цепи соответствует давлению P, а сила тока в цепи является аналогом объемной скорости кровотока Q.

Напряжение на резисторе равно

U = IR, а на конденсаторе

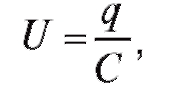
где q - величина заряда; C - емкость конденсатора. Согласно закону Кирхгофа:

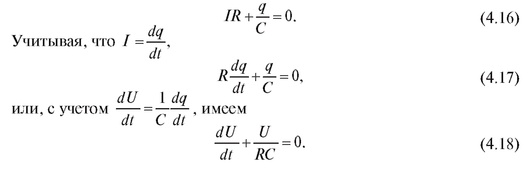
Видно, что уравнение (4.18) эквивалентно уравнению (4.12). Таким образом, электрическая модель отражает процессы, описанные в гидромеханической модели гемодинамики сосудистого русла. Данную модель можно уточнить добавлением в электрическую схему сопротивления Я1, которое моделирует сопротивление аорты (см. рис. 4.7, б).

 

4.3.3. Модель пульсовой волны

Пульсовой волной называют волну повышения давления, вызванную выбросом крови из левого желудочка в период систолы и распространяющуюся по аорте и крупным сосудам.

Пульсовая волна есть разность между систолическим и диастолическим давлениями:

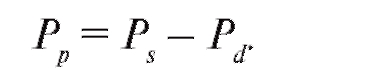(4.19)

Процессы, происходящие в крупных сосудах, описываются уравнением (4.11). Для решения этого уравнения необходимо иметь аналитическое описание функции Q(t), т. е. выброса крови из левого желудочка сердца. Для упрощения модели введем допущение, что время систолы значительно короче времени диастолы (t_S ≈ 0,3 с). В течение этого времени осуществляется выброс крови Q(t), а в фазу диастолы Q(t) = 0. Уравнение принимает вид (4.12), а его решение представлено на рис. 4.6. Согласно этой модели артериальное давление в начале сердечного цикла равно систолическому P(0) = Р_S, а в конце сердечного цикла - диастолическому P(T) = P_d Используя формулу (4.6), найдем объем крови в аорте в начале и конце сердечного цикла:

(4.20) 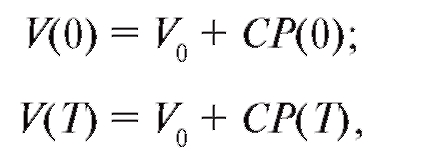(4.21)

где V₀ - «ненаполненный» объем аорты (при P = 0); T - период сердечного цикла.

Разность этих двух объемов равна ударному объему крови - объему крови, который выбрасывает левый желудочек сердца за одно сокращение.

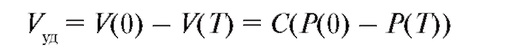(4.22) или, с учетом (4.15),

(4.23)

Тогда систолическое и диастолическое давления равны:

(4.24) 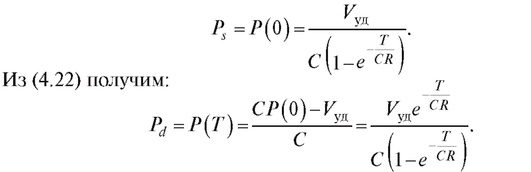(4.25)

Из уравнения (4.19) имеем:

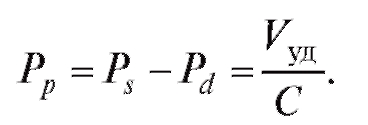(4.26)

Из уравнений (4.24) и (4.25) следует, что систолическое и диастолическое давления зависят от величины ударного объема крови, эластичности аорты, величины гидравлического сопротивления мелких сосудов и периода сокращения сердца. Это дает возможность по данной математической модели прогнозировать значения пульсовой волны, систолического и диастолического давлений при изменении перечисленных параметров сердечно-сосудистой системы.

 

По формуле (4.26), зная величину ударного объема крови, равного 60 мл, и величину пульсового давления, можно найти величину емкости артериальных сосудов:

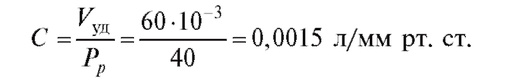
Известно, что R = 17,5 мм рт. ст./(л/мин), частота сокращений 80 уд./мин, T = 1/80 = 0,0125 мин. Подставляя в (4.24), получим P_s = 108 мм рт. ст. В норме систолическое давление равно 120 мм рт. ст., т. е. расчет, полученный на модели с учетом сделанных допущений, весьма близок к реальности.

Модель фармакокинетики лекарственного вещества

Математическая модель фармакокинетики описывает процесс изменения концентрации введенного лекарственного вещества от времени.

Для упрощения процессов, происходящих в организме при введении препарата, не рассматривается прохождение лекарства от мышцы (при внутримышечной инъекции) к органу-мишени, а также молекулярные механизмы, сопровождающие поступление, метаболизм и выведение препарата. Составим основное кинетическое уравнение уменьшения количества препарата (m) во времени в крови:

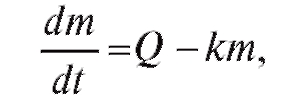(4.27)

где Q - скорость поступления препарата; km - скорость вывода препарата; k - коэффициент, зависящий от вида препарата и индивидуальных особенностей организма.

Скорость поступления препарата в кровь пациента зависит от способа его введения. При внутривенной или внутриартериальной инфузии время введения препарата значительно больше, чем при разовой инъекции, поэтому во втором случае допускаем, что Q = 0. Тогда имеем:

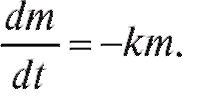(4.28)

При t = 0 масса препарата m = m₀. Получили однородное дифференциальное уравнение первого порядка. Его решение:

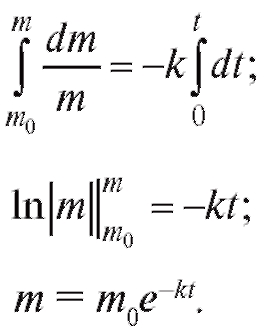(4.29)

Таким образом, после поступления препарата из мышцы в кровь начинается процесс его выведения. Этот процесс имеет экспоненциальный характер (рис. 4.8).

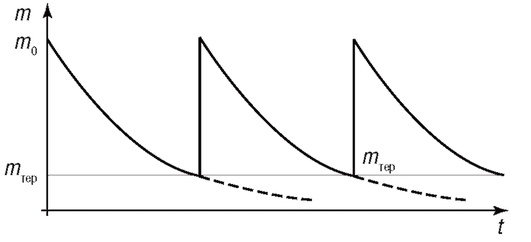
Рис. 4.8. Изменение уровня препарата в крови при периодических инъекциях

 

Для поддержания терапевтической дозы препарата необходимо дополнительное введение лекарства через определенный промежуток времени, зависящий от коэффициента k и первичной (ударной) дозы препарата (см. рис. 4.8). Из этого графика очевидно, как важно регулярно принимать лекарство для поддержания терапевтической дозы в организме.

Для поддержания постоянной концентрации препарата в крови пациента применяется непрерывное введение препарата с помощью капельницы. В этом случае Q ≠ 0 и Q = const, получим уравнение (4.27). Для его решения введем новую переменную U = Q - km, dU = -kdm, тогда

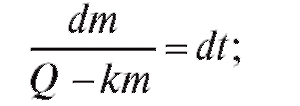(4.30)

подставим новую переменную и проинтегрируем при t = 0, m = 0.

Отсюда, потенцируя, получим: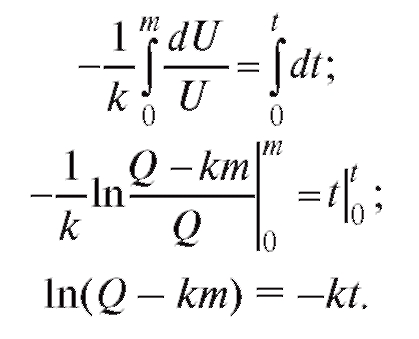

Тогда 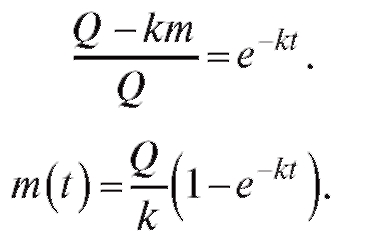(4.31)

Для перехода от массы препарата к его концентрации необходимо массу m разделить на объем крови V. Тогда

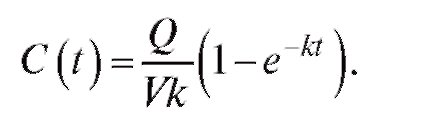(4.32)

График зависимости концентрации препарата от времени при непрерывном введении (инфузии) представлен на рис. 4.9 (линия 1). Из графика видно, что через некоторое время после введения препарата его концентрация в крови достигнет определенного уровня, который остается постоянным. Из уравнения (4.32) следует, что для достижения терапевтического уровня концентрации препарата в крови С_терскорость введения препарата равна Q = С_терVK. Однако скорость достижения этого уровня не зависит от Q, а определяется только коэффициентом k скорости введения лекарства. Поэтому для быстрого достижения уровня необходимой концентрации препарата в крови пациента (С_тер) необходимо одновременное проведение процедуры инъекции (укола) - линия 2 - и инфузии (капельницы) - линия 1. В этом случае уравнение фармакокинетики будет выглядеть как

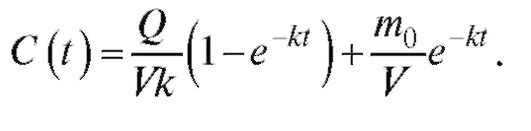(4.33)

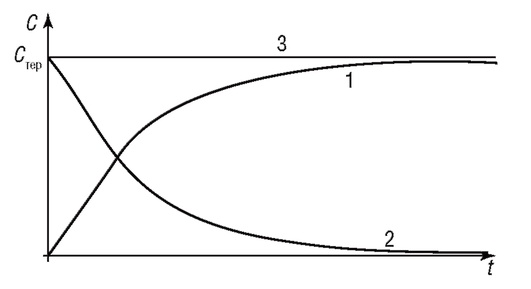
Рис. 4.9. Изменение концентрации препарата в крови организма: 1 - при непрерывном введении препарата (капельница); 2 - при одновременном введении препарата (струйная внутривенная инъекция или укол); 3 - при комбинированном введении препарата (инъекция + капельница)

 

На рис. 4.9 (линия 3) представлен график суммарной зависимости концентрации препарата при комбинированном введении препарата для случая, когда

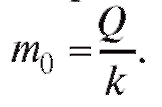
Таким образом, используя математическую модель (4.33), подбирая параметры Q, m₀ и k, можно оптимальным образом получить и поддерживать необходимую терапевтическую концентрацию лекарства в крови.

Применение фармакокинетических моделей позволяет подобрать индивидуальный режим дозирования конкретного препарата, а именно: скорость длительной инфузии препарата, подбор нагрузочной дозы, кратность введения поддерживающей дозы при дробном введении препарата.

4.3.4. Структурные модели

Одним из сложных этапов построения математических моделей является переход от описательной или концептуальной постановки задачи к математическому языку формул и уравнений. В первую очередь это справедливо в отношении сложных объектов, к которым относятся живые организмы. В этом случае возможно перейти к методам структурного моделирования, которые основаны на методах системного анализа. Под системой понимается совокупность взаимосвязанных элементов, взаимодействующих с окружающей средой и выполняющих функции, не сводимые с функциями ее элементов. Объединение элементов в систему осуществляет переход количества в качество, т. е. появление новых свойств системы, которыми не обладают элементы, входящие в систему. Поэтому одним из важных моментов изучения живых систем является выделение отдельных элементов, их связей между собой и выделение системы, которая взаимодействует с окружающей средой независимо от поведения ее отдельных элементов.

В качестве примера живых систем можно назвать клетки, органы, системы организма и весь организм в целом. Изучение этих систем методом структурного моделирования заключается в разбиении исследуемого объекта на отдельные элементы и установление связи между ними. Кроме того, устанавливаются связи системы с окружающей средой в виде реакции системы на входные сигналы. Таким образом, при структурном моделировании осуществляется выделение отдельных элементов системы и описание их функций, а затем осуществляется синтез, т. е. объединение их в единое целое. Именно анализ (разбиение) и синтез (соединение) отдельных элементов в единую систему и является целью построения структурной модели, изучение которой позволит получить новую информацию об исследуемом объекте.

 

В качестве примера рассмотрим построение структурных моделей биологических тканей.

Биологические ткани являются композитными системами с анизотропными свойствами и сложным строением. Различают пассивные и активные механические свойства биологических тканей. Пассивные механические свойства определяются физическими свойствами веществ, из которых они состоят. Основными компонентами биологических тканей являются мышечные клетки, коллаген и эластин. Коллаген представляет собой молекулярное соединение, волокнистый белок, способный растягиваться до 10% подобно капроновому волокну. Эластин - такой же волокнистый белок, но способен растягиваться до 200-300%, примерно как резина. Поэтому биологические ткани относятся к вязкоупругим системам.

Упругие и вязкие свойства тел можно моделировать отдельными элементами. При воздействии на тело растягивающей силы F (рис. 4.10, е) в моделях происходит изменение длины, которое отражено на графиках рис. 4.10 справа.

Упругий элемент можно моделировать с помощью структурного элемента в виде обычной пружины (рис. 4.10, а), которая при малых деформациях подчиняется закону Гука. График относительного удлинения пружины при F = const полностью повторяет приложенное напряжение.

За модель вязкого элемента можно принять структурный элемент, состоящий из цилиндра, заполненного вязкой жидкостью, внутри которого перемещается поршень (см. рис. 4.10, б). Вне зависимости от усилия, приложенного к поршню, относительная деформация пропорциональна времени действия силы, и по окончанию действия тело остается в растянутом положении (см. рис. 4.10, б).

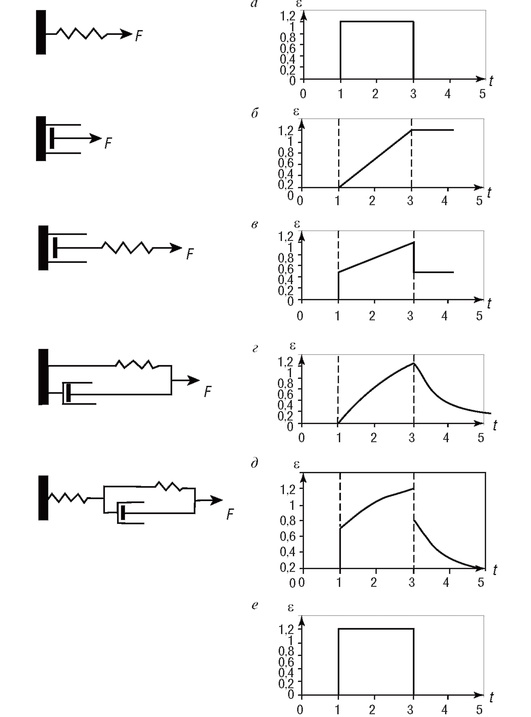
Рис. 4.10. Структурные модели вязкоупругих свойств тканей: а - упругий элемент; б - вязкий элемент; в - модель Максвелла; г - модель Фойгта; д - модель Кельвина; е - график воздействия на тело растягивающей силы

 

Исходя из этих двух элементов, формируя различные комбинации соединения структурных элементов, можно строить структурные модели тканей с различными вязкоупругими свойствами. Свойства полученных моделей в значительной степени зависят от способа соединения различных компонентов. Система, состоящая из последовательно соединенных пружин и поршня в вязкой жидкости, называется моделью Максвелла. В этой модели при создании напряжения вначале мгновенно растягивается пружина, а затем за счет сокращения пружины происходит перемещение поршня. После снятия нагрузки сохраняется остаточная деформация (см. рис. 4.10, в).

Модель Фойгта представляет систему, в которой пружина соединена с поршнем параллельно. Приложенная сила одновременно вытягивает поршень и растягивает пружину. При этом относительное удлинение носит нелинейный характер, а после снятия усилия пружина сжимается и втягивает поршень обратно (см. рис. 4.10, г).

Объединение модели Фойгта и упругой пружины получило название модели Кельвина (рис. 4.10, д). При действии внешней силы пружина 1 быстро удлиняется, а затем вытягивает поршень, при этом относительное удлинение имеет нелинейный характер. После снятия напряжения происходит быстрое сокращение пружины 1, а затем сокращение пружины 2 приводит к постепенному втягиванию поршня.

С помощью рассмотренных моделей можно изучать пассивные механические свойства биологических тканей. Для этого изучают механические характеристики конкретных биологических тканей и сравнивают их с характеристиками рассмотренных моделей. Те модели, характеристики которых наиболее близки к характеристикам биологических тканей, могут быть использованы для изучения вязкоупругих свойств тканей. В качестве механических характеристик используется чаще всего изотонический режим, т. е. изменение длины ткани во времени при действии постоянной растягивающей силы (кривая ползучести). Второй режим называется изометрическим, когда ступенчато меняют длину объекта и измеряют изменение во время внутреннего напряжения образца. Сравнение этих двух характеристик биологических тканей с аналогичными характеристиками рассмотренных моделей позволяет выбрать адекватную модель для дальнейшего изучения.

 

Костная ткань. Кость представляет собой композиционный материал, основа которого состоит из минерального вещества - гидроксиапатита.

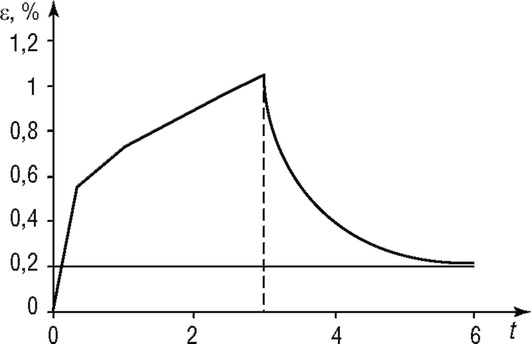
Рис. 4.11. Кривая ползучести костной ткани

Остальная часть представлена коллагеном. По механическим характеристикам костная ткань близка к твердым материалам. График кривой ползучести компактной костной ткани приведен на рис. 4.11. Из рисунка видно, что при снятии нагрузки образец кости полностью не восстанавливается в прежних размерах. Сравнение этой зависимости с кривыми ползучести рассмотренных моделей приближенно соответствует модели Кельвина (см. рис. 4.10, д). Однако в этой модели отсутствует остаточная деформация.

Кожа. Состоит из волокон коллагена, эластина и основной ткани. Обладает высокоэластичными свойствами, хорошо растягивается и удлиняется.

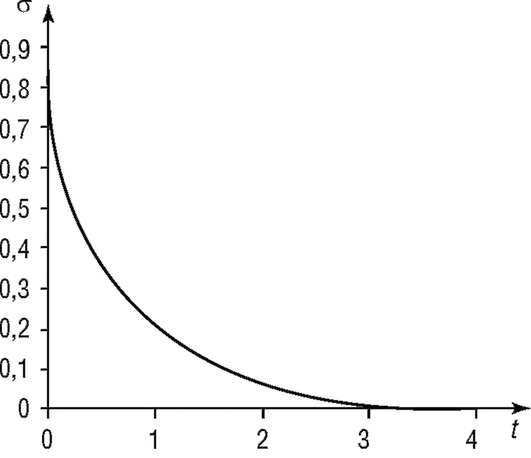
Рис. 4.12. Изменение напряжения в модели Максвелла

Для моделирования свойств кожного покрова ближе всего подходит модель Максвелла (см. рис. 4.10, в). Эта модель также хорошо подходит для моделирования характеристик гладких мышц, стенок полых органов (желчного и мочевого пузыря, желудка, кишечника, венозных и лимфатических сосудов), которые обычно испытывают длительные растягивающие усилия. Благодаря способности к деформациям полые органы способны сильно растягиваться без развития напряжения, что характерно для модели Максвелла, зависимость напряжения от времени которой показана на рис. 4.12.

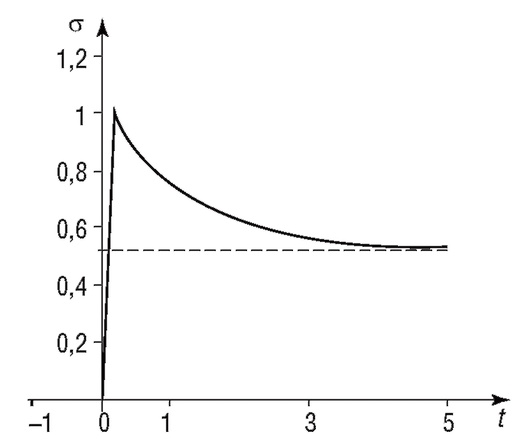
Рис. 4.13. Изменение напряжения в модели Кельвина

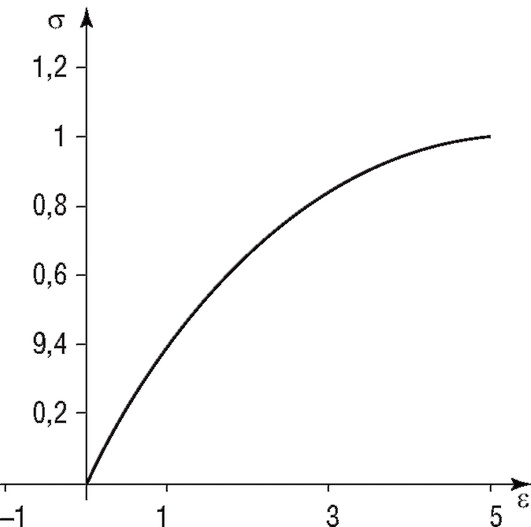
Рис. 4.14. Зависимость напряжения от удлинения скелетной мышцы

В отличие от гладких мышц, в скелетных мышцах при их быстром растяжении напряжение резко возрастает, а затем уменьшается до некоторого остаточного значения. Такая характеристика аналогична свойствам модели Кельвина (рис. 4.13). Однако в отличие от этой модели растяжение скелетной мышцы характеризуется нелинейной зависимостью напряжения от длины (рис. 4.14).

Таким образом, построение структурных моделей позволяет качественно представлять свойства биологических тканей и изучать их поведение при различных режимах нагрузки.

 

4.3.5. Имитационное моделирование

Получение новой информации об исследуемом процессе или явлении с помощью математической модели возможно путем имитационного моделирования.

Имитационное моделирование - это метод исследования, при котором изучаемая система заменяется математической моделью, с достаточной точностью описывающей реальную систему, и с ней проводятся эксперименты на ЭВМ с целью получения информации об этой системе. Экспериментирование с моделью называют имитацией (имитация - это постижение сути явления, не прибегая к экспериментам на реальном объекте).

Модель изучаемого объекта представляется в формализованном виде, а именно, в виде формул, уравнений, графиков, структурных схем, а затем на компьютере проигрываются различные варианты ситуаций, в которых может находиться эта система. Изменяются входные воздействия или внутреннее состояние системы и анализируется реакция модели в виде выходного сигнала. Обычно такие изменения выходят из диапазона входных сигналов, которые исследовались при построении модели.

Если модель адекватно отражает те стороны объекта, которые интересуют исследователя, то можно получить новую информацию об исследуемом объекте. Хотя на реальном объекте такую информацию получить сложно, так как такие воздействия могут привести к опасным последствиям для объекта. Изменяя различные управляющие воздействия, можно получить ответ на оптимальный выход системы из критического состояния. Поэтому имитационное моделирование позволяет проводить эксперименты в режиме диалога «человек-компьютер» с целью выбора наиболее эффективных методов управления биообъектом.

 

Основные этапы имитационного моделирования следующие.

• Определяются основные цели построения модели и вопросы, на которые должны получить ответ в процессе имитационного моделирования.

• Учитывая сложность моделируемой системы, производится декомпозиция объекта на отдельные блоки, взаимодействующие друг с другом. Определяются входные и выходные сигналы каждого блока и их функциональные или вероятностные зависимости.

• Определяются правила или алгоритмы функционирования отдельных блоков, а также их взаимодействие друг с другом.

• Модели функциональных блоков соединяют в единую модель системы на основе выбранного математического обеспечения. Проверяется функционирование как отдельных блоков, так и всей модели в целом, которая имитирует поведение реальной сложной системы.

• Вводится параметр времени, который позволяет моделировать процессы как в ускоренном, так и в замедленном масштабе времени.

• Далее проводят эксперименты с моделью. Полученные результаты анализируются специалистами, хорошо знающими реальную систему, которые дают заключение об адекватности модели. В дальнейшем производится коррекция модели в соответствии с заключением специалистов, расширяется диапазон входных воздействий и внутренних состояний системы. Тем самым наряду с получением новой информации идет процесс усовершенствования модели и расширения ее возможностей.

Таким образом, по результатам имитационного моделирования можно делать выводы в отношении правильности гипотезы о механизмах функционирования отдельных блоков и всей системы в целом, прогнозировать поведение системы при изменении входных воздействий и внутренних состояний, а также оценивать эффективность различных управляющих воздействий.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Приведите определение модели.

2. Какие модели используются в медицине?

3. Каково преимущество математических моделей?

4. Что дает математическое моделирование в медицине?

5. Опишите особенности живых систем по сравнению с неживыми.

6. Перечислите этапы построения математической модели.

7. Приведите определение системы.

8. В чем заключается метод структурного моделирования?

9. Назовите основные этапы имитационного моделирования.

10. Приведите возможные результаты имитационного моделирования.

ЛИТЕРАТУРА

1. Введение в математическое моделирование: учеб. пособие / под ред. П.В. Трусова. - М.: Логос, 2014. - 440 с.

2. Владимирский Ю.А., Рощункин Д.И., Потапенко А.Я. и др. Биофизика: учебник. - М.: Медицина, 1983. - 276 с.

3. Герман И. Физика организма человека: пер. с англ.; науч. издание. - Долгопрудный: ИД «Интеллект», 2011. - 992 с.

4. Омельченко В.П., Демидова А.А. Практикум по медицинской информатике. учеб. пособие. - Ростов-н/Д: Феникс, 2001. - 304 с.

5. Физика и биофизика: учебник / под ред. В.Ф. Антонова. - М.: ГЭОТАР-Медиа, 2008. - 480 с.