Термодинамика, статистическая физика и квантовая механика
Учебное пособие
Издательство Нижегородского университета
Нижний Новгород
ББК
УДК
Я
Янкина А.А., Ефремов Г.Ф.
Уровневые физические задачи: термодинамика, статистическая физика и квантовая механика. Учебное пособие. Н.Новгород:
Издательство Нижегородского университета, 1998. с.
Рецензенты:
Доцент кафедры теоретической физики НГПУ Ю.Г. Шондин
Доцент кафедры математики радиофака ННГУ А.А. Дубков
В пособии приведены трёхуровневые физические задачи, каждая из которых представляет три связанные задачи, касающиеся одного физического явления. Задача первого уровня связана с известным алгоритмом решения (стандартная ситуация), задача второго уровня предполагает изменение стандартного алгоритма решения. Задача третьего уровня связана с разработкой нового алгоритма решения и часто требует проведения некоторого исследования.
Пособие предназначено для студентов и магистрантов физических специальностей и может быть использовано на спецкурсах, при проведении рейтинговой оценки знаний студентов и при подготовке к государственному экзамену по физике.
 без объявл. ББК
без объявл. ББК
ISBN5 – 8574-287-8
 Янкина А.А.,
Янкина А.А.,
Ефремов Г.Ф., 1998
Предисловие
Предлагаемое пособие содержит трёхуровневые физические задачи по термодинамике, статистической физике и квантовой механике.
Основу данного пособия составляют существенно переработанные задачи из сборников задач по термодинамике, статистической физике и теоретической физике Ф.Г.Серовой, А.А.Янкиной (1975г., 1976г., 1979г.). Особенность данного пособия заключается в том, что каждая трёхуровневая задача представляет собой три связанные задачи, касающиеся одного и того же физического явления или физического объекта. Задача первого уровня предполагает использование физических законов в стандартной ситуации, задача второго уровня предусматривает хорошее понимание предыдущей задачи и умение использовать физические законы в новых условиях или при более строгом рассмотрении того же физического явления. Задача третьего уровня для своего решения требует чёткой постановки промежуточных задач для ответа на поставленный вопрос и часто проведения некоторого исследования.
Многие задачи снабжены рекомендациями, к некоторым даны указания, ко всем задачам приведены ответы. Этим преследовалась определённая цель: дать возможность студентам проявить большую самостоятельность. Необходимо подчеркнуть, что при решении уровневых задач 1) возникает новый обучающий элемент, состоящий в постановке разного уровня задач; 2) снимается «стресс от нерешённой задачи» на экзамене, т.к. задача первого уровня, как правило, по силам каждому студенту; 3) активизируется мыслительная деятельность обучаемого; 4) объективно оцениваются знания студента.
Учебное пособие предназначено для студентов и магистрантов физических специальностей университетов и может быть использовано на спецкурсах, в домашних контрольных работах, на зачётах, экзаменах, при проведении рейтинговой оценки знаний студентов и при подготовке к государственному экзамену по физике.
I. Термодинамика и статистическая физика
1. Первое начало термодинамики
1.1. Вычислить работу, совершаемую молем газа при расширении от объёма  до объёма
до объёма  , если
, если
1) газ является идеальным, а процесс расширения происходит при
постоянной температуре Т;
2) процесс расширения газа Ван-дер Ваальса, уравнение состояния которого
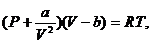
является изотермическим (Т=const);
3) процесс расширения идеального газа является адиабатическим, причём
начальная температура газа  и
и  .
.
1.2. Вычислить коэффициенты объёмного расширения  и изотермической сжимаемости
и изотермической сжимаемости  для
для
1) идеального газа при нормальных условиях (Т=273К, 
 );
);
2) газа, состояние которого описывается уравнением Ван-дер-Ваальса.
3) Используя результаты предыдущих задач, найти, при какой температуре  >
>  для случая, когда молярный объём V значительно больше поправки b.
для случая, когда молярный объём V значительно больше поправки b.
1.3. Используя тот факт, что критическому состоянию газа Ван-дер-Ваальса соответствует точка перегиба на изотерме Р(V),
1) выразить критические параметры  через постоянные
через постоянные 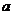 и b для этого газа.
и b для этого газа.
2) Вычислить плотность гелия в критическом состоянии, считая для него справедливым уравнение Ван-дер-Ваальса и используя значения параметров  ,
,  и критического коэффициента
и критического коэффициента  .
.
3) Найти, во сколько раз давление газа Ван-дер-Ваальса больше его критического давления, если известно, что  .
.
1.4. Идеальный газ с молярной массой  находится в цилиндрическом сосуде
находится в цилиндрическом сосуде
1) под давлением Р между дввумя одинаковыми горизонтальными пластинами. Температура газа растёт линейно от  у нижней пластины до
у нижней пластины до  у верхней. Объём газа равен V. Найти его массу;
у верхней. Объём газа равен V. Найти его массу;
2) с площадью основания S и высотой h. Температура газа Т, его давление на нижнее основание  . Считая температуру Т и ускорение свободного падения g не зависящими от высоты, найти массу газа в сосуде;
. Считая температуру Т и ускорение свободного падения g не зависящими от высоты, найти массу газа в сосуде;
3) считая в условиях предыдущей задачи  , а поле силы тяжести однородным, найти среднее значение потенциальной энергии молекулы газа.
, а поле силы тяжести однородным, найти среднее значение потенциальной энергии молекулы газа.
1.5. Используя I начало термодинамики, получите
1) уравнение политропы для идеального газа;
2) и исследуйте выражение для работы, совершаемой идеальным газом при политропическом процессе расширения, в зависимости от показателя политропы n, если теплоёмкость процесса постоянна и равна  , где
, где  ;
;
3) уравнение политропы для газа Ван-дер-Ваальса, теплоёмкость 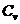 которого не зависит от температуры, а теплоёмкость политропического процесса С.
которого не зависит от температуры, а теплоёмкость политропического процесса С.
1.6. Для политропического процесса расширения идеального газа
1) выразить молярную теплоёмкость С через показатель n политропы и теплоёмкость  , представить С(n) графически;
, представить С(n) графически;
2) определить, какую долю сообщаемого газу количества тепла составляет совершаемая им работа;
3) найти соотношение между изменением внутренней энергии  и поглощённым им теплом. Газ считать двухатомным и показатель политропы n=1.32. Как меняется температура в процессе расширения газа?
и поглощённым им теплом. Газ считать двухатомным и показатель политропы n=1.32. Как меняется температура в процессе расширения газа?
1.7. Для идеального газа
1) найти максимально возможную температуру в процессе, происходящим по закону:  , где
, где  - положительные постоянные, V - молярный объём;
- положительные постоянные, V - молярный объём;
2) определить наименьшее возможное давление в процессе, уравнение которого имеет вид:  , где
, где  - положительные постоянные, V - молярный объём; изобразить в переменных P, V примерный график этого процесса;
- положительные постоянные, V - молярный объём; изобразить в переменных P, V примерный график этого процесса;
3) найти уравнение процесса, теплоёмкость которого  , где
, где  .
.
1.8. Для идеального газа, расширяющегося по закону:  , где
, где  - положительные постоянные, V - молярный объём, определить:
- положительные постоянные, V - молярный объём, определить:
1) максимально возможную температуру  ;
;
2) молярную теплоёмкость С газа как функцию его объёма V, считая  ; изобразить график С=С(V);
; изобразить график С=С(V);
3) совершённую газом работу и изменение его внутренней энергии при увеличении объёма  в 2 раза.
в 2 раза.
1.9. Идеальный газ, показатель адиабаты для которого g, расширяется так, что сообщаемое газу тепло равно убыли его внутренней энергии. Найти:
1) молярную теплоёмкость газа в этом процессе;
2) уравнение процесса в переменных T, V;
3) совершённую молем газа работу при увеличении его объёма в  раз, если начальная температура газа
раз, если начальная температура газа  .
.
1.10. Используя выражение для скорости звука  в газе через изотермическую сжимаемость
в газе через изотермическую сжимаемость  , отношение теплоёмкостей
, отношение теплоёмкостей  и плотность
и плотность  в виде
в виде  , показать, что
, показать, что
1) скорость звука в идеальном газе прямо пропорциональна  ;
;
2) температурная зависимость для  в реальном газе та же, что и в идеальном, если поправка к давлению в уравнении Ван-дер-Ваальса пренебрежимо мала.
в реальном газе та же, что и в идеальном, если поправка к давлению в уравнении Ван-дер-Ваальса пренебрежимо мала.
3) Считая распространение звука в газе адиабатическим процессом, и полагая  , получить формулу для скорости звука
, получить формулу для скорости звука  .
.
2. Второе начало термодинамики
2.1. Определить к.п.д. цикла Карно через температуры нагревателя  и холодильника
и холодильника  , если
, если
1) рабочим веществом является идеальный газ;
2) рабочим веществом является газ Ван-дер-Ваальса.
3) Показать, что к.п.д. тепловой машины  не может превышать величину
не может превышать величину 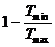 , где
, где  - максимальная температура термостатов, от которых тепловая машина получает тепло, а
- максимальная температура термостатов, от которых тепловая машина получает тепло, а  - минимальная температура резервуаров-холодильников, которым она передаёт тепло.
- минимальная температура резервуаров-холодильников, которым она передаёт тепло.
2.2. 1) В каком случае к.п.д. цикла Карно  повысится больше: при увеличении температуры нагревателя или при уменьшении температуры холодильника на одну и ту же величину?
повысится больше: при увеличении температуры нагревателя или при уменьшении температуры холодильника на одну и ту же величину?
Найти к.п.д. цикла:
2) Карно  , если при адиабатическом расширении водорода (идеального газа) объём его увеличивается в n = 2 раза;
, если при адиабатическом расширении водорода (идеального газа) объём его увеличивается в n = 2 раза;
3) состоящего из изохоры, адиабаты и изотермы, причём изотермический процесс происходит при минимальной температуре цикла и абсолютная температура в пределах цикла изменяется в n раз.
2.3. Идеальная тепловая машина работает по циклу
1) Карно. Определите  , если известно, что за один цикл производится работа 4900 Дж и холодильнику передаётся 5,4 ккал тепла;
, если известно, что за один цикл производится работа 4900 Дж и холодильнику передаётся 5,4 ккал тепла;
2) Карно и совершает за один цикл работу  Дж. Считая температуры термостатов соответственно равными
Дж. Считая температуры термостатов соответственно равными  и
и  , определить количество теплоты, получаемое рабочим веществом за один цикл от нагревателя, количество теплоты, передаваемой за каждый цикл холодильнику, и к.п.д. цикла;
, определить количество теплоты, получаемое рабочим веществом за один цикл от нагревателя, количество теплоты, передаваемой за каждый цикл холодильнику, и к.п.д. цикла;
3) Отто, состоящему из двух адиабатических и и двух изохорических процессов. Найти к.п.д. этого цикла, считая параметром его величину  - степень сжатия горючей смеси, которую можно считать идеальным газом.
- степень сжатия горючей смеси, которую можно считать идеальным газом.
2.4 1)Изображая цикл Карно на диаграмме T, S, вычислить к.п.д. этого цикла через температуры нагревателя  и холодильника
и холодильника  .
.
Найти к.п.д. обратимого цикла, в пределах которого абсолютная температура изменяется в n раз, а сам цикл имеет вид,
2) изображённый на рис.1:

Рис.1
3) изображённый на рис. 2:

Рис.2
где Т - абсолютная температура, S - энтропия.
2.5. Найти выражение молярной энтропии и уравнение адиабаты для
1) идеального газа;
2) газа, уравнение состояния которого имеет вид:  где
где  - постоянные величины,
- постоянные величины,  = const;
= const;
3) газа Ван-дер-Ваальса.
2.6. Идеальный газ с показателем адиабаты  совершает процесс по закону:
совершает процесс по закону:  , где
, где  - положительные постоянные, V - объём газа. При каком значении объёма газа
- положительные постоянные, V - объём газа. При каком значении объёма газа  энтропия будет максимальной?
энтропия будет максимальной?
2) Найти приращение энтропии для одного моля газа Ван-дер-Ваальса при изотермическом расширении его от объёма  до
до  .
.
3) Считая справедливым для теплоёмкости кристаллов С при низких температурах Т закон Дебая, согласно которому  , где
, где  найти энтропию кристалла как функцию температуры в этой области.
найти энтропию кристалла как функцию температуры в этой области.
2.7. Определить изменение энтропии одного моля идеального газа
1) в результате совершения им обратимого процесса, состоящего из двух последовательных процессов: изохорического, в котором давление меняется от  до
до  , и изобарического, в котором объём меняется от
, и изобарического, в котором объём меняется от  до
до  ;
;
2) в политропическом процессе с показателем политропы n, в результате которого абсолютная температура газа увеличивается в  раз, если известен показатель адиабаты
раз, если известен показатель адиабаты  для газа;
для газа;
3) при расширении по политропе  от объёма
от объёма  до объёма
до объёма  . Рассмотреть процессы: а) изотермический, б) адиабатический,
. Рассмотреть процессы: а) изотермический, б) адиабатический,
в) изобарический.
2.8. 1) Используя II начало термодинамики, получить дифференциальную связь термического и калорического уравнений состояния: 
2) Покажите, что внутренняя энергия вещества не зависит от объёма, если термическое уравнение состояния имеет вид:  где
где 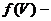 функция только объёма.
функция только объёма.
3) Плотность энергии газа является функцией только температуры Т, а уравнение состояния газа имеет вид:  Определить функциональную зависимость
Определить функциональную зависимость 
2.9. 1) Используя дифференциальную связь термического и калорического уравнений состояния для однородной системы, получить выражение внутренней энергии U(T,V) для газа Ван-дер-Ваальса, у которого 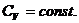
2) Покажите, что у веществ, термическое уравнение состояния которых таково, что давление является линейной функцией температуры Т, теплоёмкость  не зависит от объёма.
не зависит от объёма.
3) Вычислить разность молярных теплоёмкостей  газа Ван-дер-Ваальса, оставляя лишь линейные члены по отношению к поправкам
газа Ван-дер-Ваальса, оставляя лишь линейные члены по отношению к поправкам 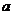 и b.
и b.
2.10. 1) Используя закон Стефана-Больцмана, найти выражение для энтропии равновесного излучения как функцию температуры и объёма.
2) Определить количество тепла 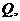 полученного равновесным излучением от нагревателя при обратимом изотермическом расширении от объёма
полученного равновесным излучением от нагревателя при обратимом изотермическом расширении от объёма  до объёма
до объёма  .
.
3) Вычислить теплоёмкости  и
и  для равновесного излучения.
для равновесного излучения.
3. Классические и квантовые функции распределения
3.1. Используя распределение Максвелла, вычислить
1) наивероятнейшую, среднюю и среднеквадратичную скорости поступательного движения молекул газа;
2) число ударов  молекул газа о единичную площадку поверхности сосуда за 1 секунду и показать, что величина
молекул газа о единичную площадку поверхности сосуда за 1 секунду и показать, что величина  где n - концентрация молекул в газе;
где n - концентрация молекул в газе;
3) давление газа на стенки сосуда, если концентрация молекул в газе равна n.
3.2. 1) Вывести термическое уравнение состояния классического идеального газа.
Используя каноническое рапределение Гиббса,
2) вычислить интеграл состояний для одноатомного идеального газа и получить уравнения состояния для этого газа;
3) вывести термическое уравнение состояния идеального одноатомного релятивистского газа, у частиц которого энергия и импульс связаны соотношением  где с - скорость света в вакууме.
где с - скорость света в вакууме.
3.3. На основе распределения Больцмана определить
1) на какой высоте в атмосфере при температуре Т=273 К давление воздуха уменьшается втрое, если молярная масса воздуха  , ускорение силы тяжести
, ускорение силы тяжести  ;
;
2) число Авогадро, если распределение взвешенных в жидкости частиц гуммигута по высоте в однородном поле силы тяжести характеризуется следующими данными: число частиц гуммигута уменьшается в 2 раза на высоте h=100 мкм при Т= 293 К, диаметр этих частиц  см, плотность гуммигута на
см, плотность гуммигута на  больше плотности жидкости;
больше плотности жидкости;
3) долю молекул кислорода ( ) земной атмосферы, способных преодолеть гравитационное поле Земли при Т=300 К.
) земной атмосферы, способных преодолеть гравитационное поле Земли при Т=300 К.
3.4. Равновесный газ находится в высоком цилиндрическом сосуде при температуре Т. Считая поле силы тяжести однородным, найти
1) среднее значение потенциальной энергии одной молекулы;
2) зависимость средней потенциальной энергии молекулы массы m от высоты Н сосуда с газом;
3) энергию и теплоёмкость 1 моля одноатомного идеального газа, находящегося в этом сосуде, если высота его Н; рассмотреть 2 предельных случая: а)  б)
б) 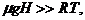 где
где  молярная масса, R - универсальная газовая постоянная.
молярная масса, R - универсальная газовая постоянная.
3.5. Потенциальная энергия молекул газа в некотором центральном поле зависит от расстояния r до центра поля как  , где
, где  . Температура газа Т, концентрация молекул в центре поля
. Температура газа Т, концентрация молекул в центре поля  . Найти:
. Найти:
1) число молекул газа, находящихся на расстоянии  от центра поля;
от центра поля;
2) наиболее вероятное расстояние  молекул от центра поля;
молекул от центра поля;
3) во сколько раз изменится концентрация молекул в центре поля при уменьшении температуры в  раз.
раз.
3.6. Потенциальная энергия молекул газа в центрально-симметричном поле описывается формулой  , где
, где  и r - расстояние от молекулы до центра поля. Считая известными температуру газа Т и концентрацию молекул n в центре поля, найти:
и r - расстояние от молекулы до центра поля. Считая известными температуру газа Т и концентрацию молекул n в центре поля, найти:
1) число молекул газа с потенциальной энергией в интервале 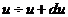 ;
;
2) наиболее вероятное значение потенциальной энергии  ; сравнить эту величину с потенциальной энергией молекулы на наиболее вероятном расстоянии её от центра поля;
; сравнить эту величину с потенциальной энергией молекулы на наиболее вероятном расстоянии её от центра поля;
3) среднее значение потенциальной энергии молекул и потенциальную энергию всего газа.
3.7. Газ из дипольных молекул находится во внешнем однородном электрическом поле с потенциальной энергией  где
где 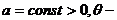 угол между векторами дипольного момента
угол между векторами дипольного момента  и напряжённости
и напряжённости  поля (
поля ( ).
).
1) Получить распределение молекул по углам  .
.
2) Вычислить среднее значение потенциальной энергии молекулы.
3) Определить, у какой части молекул аммиака ( ) при Т=273К дипольные моменты (
) при Т=273К дипольные моменты ( Кл м) образуют с направлением вектора
Кл м) образуют с направлением вектора  поля угол, не превышающий
поля угол, не превышающий 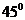 ? Величина напряжённости поля
? Величина напряжённости поля  .
.
3.8. Исходя из функции распределения по энергиям, получить:
1) распределение по скоростям для равновесного классического идеального газа; изобразить график этой функции;
2) распределение по скоростям для нерелятивистских фермионов с половинным спином; изобразить график этой функции при абсолютном нуле температуры;
3) используя результаты предыдущих задач, вычислить среднюю и среднеквадратичную скорости
а) молекул идеального газа в зависимости от температуры;
б) фермионов при Т=0К.
3.9. Получить выражение молярной теплоёмкости при постоянном объёме 
1) для классического идеального одноатомного газа;
2) для идеального одноатомного ультрарелятивистского газа ( ;
;
3) твёрдого кристаллического тела, представляя тепловые колебания N атомов решётки в виде системы 3N независимых квантовых линейных осцилляторов с собственной частотой  .
.
3.10. 1) Вычислить наиболее вероятную энергию 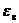 молекул в идеальном газе. Показать, что
молекул в идеальном газе. Показать, что  .
.
2) В идеальном газе фермионов определить энергию тех уровней, вероятности заполнения которых соответственно равны 0,1 и 0,9.
3) Какова вероятность заполнения электронами в металле энергетического уровня, расположенного на 0,01 эВ ниже уровня Ферми, при температуре 200К?
3.11. Пользуясь соответствующей функцией распределения для равновесного идеального газа, получить:
1) выражение средней энергии поступательного движения частицы газа;
2) уравнение состояния невырожденного (классического) газа; вычислить первую поправку в уравнении состояния идеальных газов, обусловленную квантовой статистикой;
3) основное уравнение кинетической теории. Показать справедливость этого уравнения для любых идеальных газов, независимо от степени вырождения.
3.12. Пользуясь формулой Планка для спектральной плотности энергии равновесного теплового излучения, получить:
1) закон Стефана-Больцмана:  , выразив постоянную
, выразив постоянную  через универсальные константы;
через универсальные константы;
2) закон смещения Вина:  , выразив постоянную Вина "b" через универсальные константы
, выразив постоянную Вина "b" через универсальные константы  ;
;
3) выражение для полного числа фотонов в единице объема полости, заполненной излучением. Оценить это число фотонов при Т=300К.
4. Термодинамическое равновесие и фазовые превращения
4.1. 1) Определите условия равновесия двухфазной однокомпонентной системы, находящейся в термостате (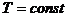 ) под постоянным внешним давлением (
) под постоянным внешним давлением ( ).
).
2) Используя результат предыдущей задачи, получить уравнение Клапейрона-Клаузиуса:

где  - удельная теплота превращения вещества из первой фазы во вторую,
- удельная теплота превращения вещества из первой фазы во вторую,  и
и  - удельные объемы вещества соответственно в первой и во второй фазах.
- удельные объемы вещества соответственно в первой и во второй фазах.
3) Найти давление насыщенного водяного пара при температуре  , считая пар идеальным газом и
, считая пар идеальным газом и  .
.
4.2. 1) Вода со своим насыщенным паром находится в сосуде объемом  при температуре
при температуре  и давлении 40 атм. Удельный объем пара при этих условиях
и давлении 40 атм. Удельный объем пара при этих условиях  , масса всей системы (вода + пар) m=5 кг. Найти массу и объем пара.
, масса всей системы (вода + пар) m=5 кг. Найти массу и объем пара.
2) Пользуясь уравнением Клапейрона-Клаузиуса, получить температурную зависимость давления насыщенного пара, если температура не слишком близка к критической, так, что  ; пар подчиняется уравнению состояния идеального газа,
; пар подчиняется уравнению состояния идеального газа,  - удельная теплота испарения, в рассматриваемом интервале температур постоянна.
- удельная теплота испарения, в рассматриваемом интервале температур постоянна.
3) Под каким давлением будет кипеть вода при температуре  , если
, если 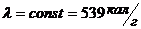 ?
?
4.3. 1) Найти удельный объем воды в жидком и парообразном состояниях при нормальных условиях.
2) Найти удельный объем насыщенного водяного пара при нормальном давлении, если известно, что уменьшение давления на величину  Па приводит к уменьшению температуры кипения воды на
Па приводит к уменьшению температуры кипения воды на  .
.
3) Определить температурную зависимость удельного объема пара для процесса, при котором пар остается в равновесии с жидкостью, т.е. вдоль кривой равновесия фаз.
4.4. 1) Найти число молекул насыщенного водяного пара, содержащихся в 1  при температуре
при температуре  .
.
2) Используя уравнение Клапейрона-Клаузиуса, определить давление  и температуру
и температуру 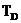 в тройной точке D (воды, пара, льда), если давление насыщенного пара над жидкой водой при
в тройной точке D (воды, пара, льда), если давление насыщенного пара над жидкой водой при  равно
равно 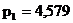 мм рт.ст., а при
мм рт.ст., а при  мм рт.ст. Удельные объемы льда и воды при
мм рт.ст. Удельные объемы льда и воды при 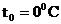 и
и  мм рт.ст. соответственно равны
мм рт.ст. соответственно равны  , удельная теплота плавления льда
, удельная теплота плавления льда  ;
;
3) найти температурную зависимость давления насыщенного пара над твердым телом, рассматривая пар идеальным газом и 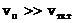 . Теплоемкости пара и твердого тела считать постоянными.
. Теплоемкости пара и твердого тела считать постоянными.
4.5. Во сколько раз плотность насыщенных паров воды при температуре  больше плотности насыщенных паров воды при температуре
больше плотности насыщенных паров воды при температуре  ?
?
2) Определить удельный объём водяного пара  при температуре
при температуре  и нормальном давлении, если известно, что при давлении
и нормальном давлении, если известно, что при давлении  мм рт.ст. температура кипения воды равна
мм рт.ст. температура кипения воды равна  . Удельная теплота парообразования при
. Удельная теплота парообразования при  равна
равна 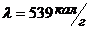 .
.
3) Насыщенный водяной пар при температуре  подвергается адиабатическому сжатию. Каким он становится: ненасыщенным или пересыщенным? Как меняется его состояние при адиабатическом расширении?
подвергается адиабатическому сжатию. Каким он становится: ненасыщенным или пересыщенным? Как меняется его состояние при адиабатическом расширении?
4.6. 1) Какая часть удельной теплоты испарения воды при температуре  идёт на увеличение внутренней энергии системы?
идёт на увеличение внутренней энергии системы?
2) Какое количество тепла необходимо сообщить воде, кипящей при нормальном атмосферном давлении, чтобы превратить  кг воды в пар?
кг воды в пар?
3) Насыщенный водяной пар находится при температуре  в цилиндрическом сосуде под невесомым поршнем. При медленном вдвигании поршня небольшая масса пара
в цилиндрическом сосуде под невесомым поршнем. При медленном вдвигании поршня небольшая масса пара  г сконденсировалась. Какая работа была совершена над паром? Пар считать идеальным газом, объёмом жидкости пренебречь.
г сконденсировалась. Какая работа была совершена над паром? Пар считать идеальным газом, объёмом жидкости пренебречь.
4.7. 1) Удельная теплота испарения бензола (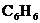 ) при температуре
) при температуре  равна
равна  . Чему равно изменение внутренней энергии при испарении 20 г бензола при этой температуре?
. Чему равно изменение внутренней энергии при испарении 20 г бензола при этой температуре?
2) Пользуясь уравнением Клапейрона-Клаузиуса, вычислить удельную теплоту испарения воды при температуре  , если известны давления водяных паров при температурах, близких к температуре кипения:
, если известны давления водяных паров при температурах, близких к температуре кипения: 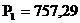 мм рт.ст. при
мм рт.ст. при  ,
,  мм рт.ст. при
мм рт.ст. при  . Удельные объёмы пара и воды при температуре
. Удельные объёмы пара и воды при температуре  соответственно равны
соответственно равны  ,
,  .
.
3) Получить температурную зависимость молярной теплоты перехода  из одной фазы в другую, считая известным изменения молярного объёма
из одной фазы в другую, считая известным изменения молярного объёма  и молярной теплоёмкости
и молярной теплоёмкости  .
.
4.8. 1) Температура плавления олова при давлении в  равна
равна  , а при давлении
, а при давлении 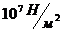 она равна
она равна  . Плотность жидкого олова
. Плотность жидкого олова  . Найти увеличение энтропии при плавлении 1 кмоля олова.
. Найти увеличение энтропии при плавлении 1 кмоля олова.
2) Найти изменение энтропии льда массой 1 кг при его превращении в пар, если начальная температура льда  , температура пара
, температура пара  . Теплоёмкость воды и льда считать постоянными, а все процессы происходящими при атмосферном давлении. Удельная теплоёмкость льда, удельные теплоты плавления и парообразования соответственно равны:
. Теплоёмкость воды и льда считать постоянными, а все процессы происходящими при атмосферном давлении. Удельная теплоёмкость льда, удельные теплоты плавления и парообразования соответственно равны: 
 ,
,  .
.
3) Найти температурную зависимость удельной энтропии неоднородной системы, состоящей из жидкости и её насыщенного пара. Считать удельную теплоёмкость жидкости 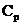 не зависящей от температуры.
не зависящей от температуры.
4.9. 1) Показать, что при критической температуре удельная теплота парообразования (теплота перехода из жидкой фазы в газообразную) равна нулю.
2) Используя известное выражение для теплоёмкости однородной системы в виде:  , выразить удельную теплоёмкость
, выразить удельную теплоёмкость  в критической точке системы жидкость-пар через плотность вещества
в критической точке системы жидкость-пар через плотность вещества  и скорость звука
и скорость звука  .
.
3) На основе результатов предыдущей задачи определить  в критическом состоянии для газа Ван-дер-Ваальса.
в критическом состоянии для газа Ван-дер-Ваальса.
4.10. 1) Выразите критическую температуру 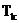 для газа Ван-дер-Ваальса через постоянные
для газа Ван-дер-Ваальса через постоянные 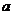 и b этого газа, оцените
и b этого газа, оцените 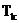 для кислорода.
для кислорода.
2) Используя выражение для дифференциального эффекта Джоуля-Томсона, получите связь между температурой инверсии 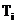 и критической температурой
и критической температурой 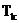 для газа Ван-дер-Ваальса.
для газа Ван-дер-Ваальса.
3) Покажите, что газ, подчиняющийся уравнению Ван-дер-Ваальса с коэффициентом  , в процессе Джоуля-Томсона всегда нагревается. Объясните, почему это происходит, и найдите изменение температуры при расширении.
, в процессе Джоуля-Томсона всегда нагревается. Объясните, почему это происходит, и найдите изменение температуры при расширении.
II. Квантовая механика
5. Частица в потенциальной яме. Туннельный эффект
5.1. Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна 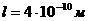 .
.
Найти:
1) с помощью соотношения неопределённостей минимально возможную энергию;
2) энергетический спектр электрона в стационарных состояниях;
3) число энергетических уровней в интервале ( ) и длину волны фотона, испускаемого при переходе
) и длину волны фотона, испускаемого при переходе  .
.
5.2. Для частицы в одномерной прямоугольной потенциальной яме с
абсолютно непроницаемыми стенками и шириной 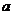
1) найти нормированные волновые функции стационарных состояний;
2) вычислить вероятность её нахождения с наименьшей энергией в области  ;
;
3) вычислить  и получить соотношение неопределённостей для координаты x и импульса
и получить соотношение неопределённостей для координаты x и импульса  .
.
5.3. В одномерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками и шириной 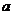 находится электрон, состояние которого описывается волновой функцией
находится электрон, состояние которого описывается волновой функцией  . Определить:
. Определить:
1) нормировочную постоянную А;
2) среднее значение кинетической энергии электрона;
3) вероятность пребывания электрона в основном состоянии.
5.4. Частица массой  находится в двухмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (
находится в двухмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (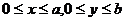 ). Найти:
). Найти:
1) с помощью соотношения неопределённостей минимально возможную энергию;
2) энергетический спектр частицы в стационарных состояниях;
3) вероятность её нахождения в области  для основного состояния.
для основного состояния.
5.5. Частица массой  находится в трёхмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (
находится в трёхмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (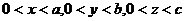 ). Найти:
). Найти:
1) с помощью соотношения неопределённостей минимально возможную энергию частицы;
2) волновые функции стационарных состояний и энергетический спектр частицы в яме;
3) значения энергии первых трёх уровней и кратность их вырождения в кубической яме ( ).
).
5.6. Для частицы массой  , находящейся на n-ом энергетическом уровне в
, находящейся на n-ом энергетическом уровне в
одномерной прямоугольной потенциальной яме с абсолютно непрони-
цаемыми стенками
1) вычислить средние значения  и
и  ;
;
2) определить средние значения квадрата импульса  и кинетической энергии
и кинетической энергии  ;
;
3) получить распределение вероятностей по импульсам.
5.7.Частица массой  находится в потенциальной яме (рис.1):
находится в потенциальной яме (рис.1):

 |
Рис.1
1) Получить уравнение, определяющее энергетический спектр собст-
венных значений энергии частицы в области  , и привести его
, и привести его
к виду  где
где  ;
;
2) обосновать дискретность энергетического спектра для  определить значение параметра ямы
определить значение параметра ямы  , при котором появляется n-й дискретный уровень;
, при котором появляется n-й дискретный уровень;
3) на основе результатов предыдущих задач найти значение  , при котором энергия единственного уровня равна
, при котором энергия единственного уровня равна  . Какова при этом вероятность нахождения частицы вне ямы?
. Какова при этом вероятность нахождения частицы вне ямы?
5.8.Частица массы  движется в одномерной прямоугольной потенциаль-
движется в одномерной прямоугольной потенциаль-
ной яме 
1) Получить уравнение, определяющее спектр собственных значений
энергии. В области  обосновать дискретность энергетического спектра.
обосновать дискретность энергетического спектра.
2) Найти значение параметра ямы  , при котором энергия основ -
, при котором энергия основ -
ного состояния частицы 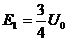 .
.
3) Определить число энергетических уровней в яме, если  .
.
5.9.Частица массой  движется в потенциальном поле вида
движется в потенциальном поле вида

1) Найти волновую функцию частицы с энергией  ;
;
2) В условиях предыдущей задачи вычислить коэффициенты отражения R и прозрачности D;
3) доказать, что для частицы с энергией  коэффициент отражения барьера
коэффициент отражения барьера  .
.
5.10.Частица массой  , имеющая энергию
, имеющая энергию  , движется слева напра-
, движется слева напра-
во в потенциальном поле вида 
1) Найти коэффициенты прозрачности D и отражения R;
2) используя результат предыдущей задачи, определить величину энергии E, при которой частица будет беспрепятственно проходить через яму. Установить для этого случая связь между шириной ямы 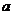 и длиной волны де-Бройля
и длиной волны де-Бройля  внутри ямы;
внутри ямы;
3) вычислить при заданных значениях  и
и  ширину ямы
ширину ямы 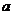 , при которой коэффициент отражения ямы максимален.
, при которой коэффициент отражения ямы максимален.
5.11.Частица массой  и энергией E падает на прямоугольный барьер
и энергией E падает на прямоугольный барьер

1) Найти для случая  коэффициенты прозрачности D и отра -
коэффициенты прозрачности D и отра -
жения R;
2) вычислить коэффициент прозрачности D при  ;
;
3) определить первые два значения энергии E, при которых частица (электрон) беспрепятственно проходит через барьер, если 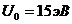 и
и  м.
м.
5.12.Для частицы массой  , падающей на прямоугольный барьер
, падающей на прямоугольный барьер

1) найти коэффициент прозрачности D, если полная энергия частицы
 ;
;
2) упростить полученное выражение D в предыдущей задаче для
случая, когда  ;
;
3) вычислить коэффициент прозрачности D барьера, если в качестве
частицы выступает электрон с энергией 10 эВ, высота и ширина
барьера равны соответственно  и
и  м. Каков ко-
м. Каков ко-
эффициент прозрачности того же барьера для протона с энергией
10эВ?
5.13.1) Обобщить формулу коэффициента прозрачности D прямоугольно-
го барьера на случай одномерного барьера произвольной формы;
2) используя результат предыдущей задачи, вычислить коэффициент
прозрачности барьера, изображённого на pис. 2, для частицы массой  с энергией
с энергией  ;
;
3) для частицы массой  и энергией
и энергией  найти коэффициент прозрачности D барьера, заданного потенциальной кривой
найти коэффициент прозрачности D барьера, заданного потенциальной кривой 
 |
Рис.2
6. Квантовый гармонический осциллятор
6.1. Частица массы m движется в одномерном потенциальном поле
 (гармонический осциллятор). Найти энергию частицы в ос-
(гармонический осциллятор). Найти энергию частицы в ос-
новном состоянии с помощью
1) соотношения неопределённостей ( );
);
2) уравнения Шрёдингера, если волновая функция частицы в этом состоянии  , где А – нормировочный коэффициент,
, где А – нормировочный коэффициент,  ;
;
3) в условиях предыдущей задачи оценить кинетическую энергию осциллятора. Вычислить среднее значение его потенциальной энергии.
6.2. Для линейного гармонического осциллятора с частотой  и массой m
и массой m
1) привести уравнение Шрёдингера для стационарных состояний к виду:  , где безразмерная переменная
, где безразмерная переменная  ;
;
2) найти собственные значения энергии, зная, что параметр 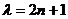 , где
, где 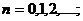
3) проиллюстрировать принцип соответствия, используя формулу энергетического спектра.
6.3. Стационарное состояние линейного гармонического осциллятора с частотой  и массой m описывается волновой функцией
и массой m описывается волновой функцией  , где
, где
 . Вычислить
. Вычислить
1) нормировочный коэффициент А;
2) средние значения координаты  и импульса
и импульса  ;
;
3) средние квадратичные отклонения  и
и  , проверив соотношение неопределённостей для координаты x и импульса
, проверив соотношение неопределённостей для координаты x и импульса  .
.
6.4. Стационарные состояния линейного гармонического осциллятора с частотой  и массой m описывается волновыми функциями
и массой m описывается волновыми функциями
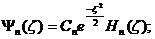 где n = 0, 1, 2,…, безразмерная координата
где n = 0, 1, 2,…, безразмерная координата
 , полином Эрмита
, полином Эрмита 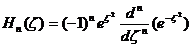 . Вычислить:
. Вычислить:
1) нормировочный коэффициент  ;
;
2) среднее значение  и среднюю потенциальную энергию в n-м энергетическом состоянии
и среднюю потенциальную энергию в n-м энергетическом состоянии  ;
;
3) среднюю кинетическую энергию осциллятора  .
.
6.5. Для трёхмерного гармонического осциллятора с массой m и потенци -
альной энергией 
1) с помощью соотношений неопределённостей оценить энергию нуле-
вых колебаний;
2) найти волновые функции стационарных состояний и спектр собст-
венных значений энергии;
3) пользуясь результатами предыдущей задачи, записать формулу энергетического спектра изотропного гармонического осциллятора ( ). Какова кратность вырождения квантового энергетического уровня
). Какова кратность вырождения квантового энергетического уровня  ?
?
6.6. Линейный гармонический осциллятор с частотой  , массой m и зарядом е помещён в постоянное однородное электрическое поле
, массой m и зарядом е помещён в постоянное однородное электрическое поле  .
.
1) Найти потенциальную энергию заряженного осциллятора и записать стационарное уравнение Шрёдингера;
2) какую новую переменную следует ввести, чтобы преобразовать стационарное уравнение Шрёдингера к виду, известному для случая отсутствия электрического поля?
3) Найти энергетический спектр и волновые функции стационарных состояний.
6.7. Стационарное состояние линейного гармонического осциллятора с частотой  и массой m описывается волновой функцией
и массой m описывается волновой функцией  .
.
1) Найти значение параметра  и энергию E осциллятора;
и энергию E осциллятора;
2) вычислить наиболее вероятное значение координаты x;
3) изобразить примерный график распределения плотности вероятности  различных значений x в этом состоянии.
различных значений x в этом состоянии.
6.8. Линейный гармонический осциллятор находится в стационарном со-
стоянии с наименьшей энергией. Найти:
1) наиболее вероятное значение координаты  у осциллятора;
у осциллятора;
2) значения координаты  , соответствующие границам классической области движения осциллятора; изобразить примерный график распределения плотности вероятности
, соответствующие границам классической области движения осциллятора; изобразить примерный график распределения плотности вероятности  различных значений x в этом состоянии;
различных значений x в этом состоянии;
3) вероятность пребывания осциллятора вне классических границ.
7. Движение в центрально-симметричном поле. Атом водорода
7.1. 1) Для операторов проекций момента импульса
 показать,
показать,
что коммутатор  ;
;
2) объяснить, почему невозможны состояния с определённым вектором
момента импульса 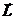 ;
;
3) вычислить коммутатор оператора квадрата импульса 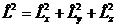
с оператором  . Каков физический смысл полученного результата?
. Каков физический смысл полученного результата?
7.2. Для частицы, движущейся в центрально-симметричном поле
1) получить выражение оператора  в сферических координатах, выбрав ось OZ в качестве полярной оси;
в сферических координатах, выбрав ось OZ в качестве полярной оси;
2) определите собственные функции и собственные значения оператора  , найденного в предыдущей задаче.
, найденного в предыдущей задаче.
3) Частица находится в состоянии, описываемом волновой функцией
 2017-12-14
2017-12-14 1570
1570