Лекция 7. Марковские модели надежности

В лекции 1 все модели надежности были разделены на два класса статические и динамические. Статическая модель описывает “надежностное” состояние системы в момент времени t набором работоспособных и неработоспособных элементов. Лекции 4-9 были посвящены методам анализа, используемым в статических моделях. В лекциях 4 и 5, посвященных блок-схемам надежности, рассматривалось применение основных формул теории вероятностей (вероятность суммы и произведения событий, формула полной вероятности) для расчета показателей надежности резервированных невосстанавливаемых систем. В лекциях 6-9 изучались логико-вероятностные методы анализа надежности, основанные на записи логических условий работоспособности (неработоспособности) и их последующего преобразования в вероятностную форму. Эти методы оказываются недостаточными для исследования сложных систем. С точки зрения анализа надежности сложность систем обуславливается следующими факторами:

наличие нескольких уровней эффективности функционирования (производительности) в работоспособных состояниях и постепенная деградация по эффективности при возникновении неисправностей; состояния неработоспособности могут также различаться по последствиям
реализация разнообразных способов резервирования (структурного, временного, алгоритмического)
использование различных стратегий восстановления. Ограничение на ЗИП и число ремонтных бригад.
применение алгоритмических методов обработки неисправностей (в основном для вычислительных устройств) с классификацией на сбои и отказы
возможность возникновения нескольких несовместных видов отказов элементов, приводящих при определенной кратности и последовательности возникновения к различным последствиям на системном уровне; наличие скрытых и явных отказов
отказы по общей причине, индуцированные отказы.

Учет перечисленных факторов возможен в рамках динамических моделей надежности, описывающих происходящие в системе события, отказы как процессы, развивающиеся во времени. Наиболее распространенными динамическими моделями “надежностного” поведения систем являются марковские и полумарковские случайные процессы. Данная и последующие лекции курса будут посвящены использованию марковских моделей надежности для анализа сложных систем с восстановлением.

I. Марковские случайные процессы

В теории вероятностей введено понятие случайной функции, т.е. такой функции, значение которой при каждом данном значении аргумента (или аргументов) является случайной величиной. Случайную функцию можно рассматривать как совокупность случайных величин, представляющих ее значения при различных значениях аргумента. В общем случае случайная функция равноценна бесконечному, несчетному множеству случайных величин.

Каждая конкретная функция, которая может быть зарегистрирована при одном наблюдении случайной функции, называется реализацией этой функции.

Случайная функция времени характеризует процесс изменения случайной величины с течением времени. Случайные функции времени называют случайными или стохастическими процессами.

Говорят, что в некоторой системе S протекает случайный процесс, если ее состояния меняются с течением времени случайным образом. Процесс, протекающий в системе, называется марковским или процессом без последействия, если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние.

Пространство возможных состояний системы может быть как непрерывным, так и дискретным, когда состояния системы можно перечислить или пронумеровать. При исследовании надежности систем, состоящих из элементов с заданными надежностными характеристиками, пространство состояний всегда дискретно.

Математическое описание марковского случайного процесса, протекающего в системе с дискретными состояниями, зависит от того, в какие моменты времени могут происходить переходы системы из состояния в состояние. Если переходы между состояниями могут происходить только в заранее определенные моменты времени, то такой процесс называют марковским процессом с дискретным временем. Если переходы могут происходить в любые случайные моменты времени, то такой процесс называют марковским процессом с непрерывным временем. При экспоненциальном распределении случайного времени пребывания системы в каждом из своих состояний марковский процесс является однородным (интенсивности переходов между состояниями не зависят от времени). Однородные марковские процессы с дискретным множеством состояний и непрерывным временем являются основным аппаратом исследования надежности сложных систем с восстановлением. Это объясняется тем, что именно они позволяют получать аналитические выражения или конструктивные вычислительные схемы для расчета различных показателей надежности. Кроме того, в подавляющем большинстве случаев исходными данными для элементов являются либо константные интенсивности отказов, либо средние наработки до отказа.

Построение марковских моделей надежности происходит следующим образом. На основе информации о структуре и принципах функционирования исследуемой системы определяется множество ее возможных состояний. Это множество разделяется на два подмножества – работоспособных состояний и состояний отказа. Далее строится марковский граф переходов, вершинами которого являются состояния системы, а ребрами – возможные переходы между состояниями. Интенсивности переходов определяются характеристиками безотказности и ремонтопригодности элементов системы. По графу переходов составляется необходимая система уравнений, решение которой позволяет получить требуемые показатели надежности.

II. Уравнение Колмогорова-Чепмена. Марковская модель надежности восстанавливаемого элемента.

Рассмотрим функционирование восстанавливаемого элемента, при следующих предположениях: (1) поток отказов элемента – пуассоновский с параметром l (интенсивность отказов); (2) поток восстановлений элемента - пуассоновский с параметром m (интенсивность восстановления). Предположения (1) и (2) равносильны предположению об экспоненциальном распределении случайных времен отказа и восстановления. Элемент может находиться в двух состояниях: 1 - исправное состояние; 2 – состояние отказа. Марковский граф переходов элемента между исправным состоянием и состоянием отказа показан на рис.1.

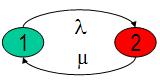
Рис.1. Марковский граф переходов восстанавливаемого элемента.

Обозначим: P₁(t) – вероятность нахождения элемента в момент времени t в состоянии 1. P₂(t) – вероятность нахождения элемента в момент времени t в состоянии 2. Событие A работоспособности элемента (нахождения в состоянии 1) в момент времени t+Dt может произойти двумя способами. Либо произойдет событие B, состоящее в том, что в момент t элемент уже находился в работоспособном состоянии 1 и за время Dt не вышел из этого состояния (отказ за Dt не произошел). Либо произойдет событие С, состоящее в том, что в момент t элемент была в состоянии отказа 2 и за время Dt перешел из состояния 2 в состояние 1 (работоспособность элемента была восстановлена за Dt).

Вероятность события B равна

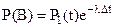(1)

Разлагая экспоненту в ряд, получаем .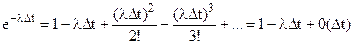

Или с точностью до величин высшего порядка малости

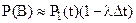(2)

Вероятность события С равна

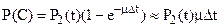(3)

Тогда вероятность события А (работоспособности элемента в момент времени t+Dt), с учетом того, что события B и C несовместны, определяется как:

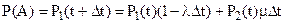(4)

Если мы перенесем P₁(t) в левую часть уравнения, разделим полученное приращение функции на приращение аргумента, устремив Dt к нулю, то получим дифференциальное уравнение относительно неизвестной вероятности P₁(t):

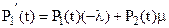(5)

Аналогично рассуждая, можно получить дифференциальное уравнение относительно вероятности P₂(t). Таким образом, мы получили для вероятностей P₁(t) и P₂(t) систему обыкновенных дифференциальных уравнений:

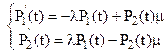(6)

Полученную систему дифференциальных уравнений решают при начальных условиях P₁(0), P₂(0), задающих распределение вероятностей состояний в начальный момент времени t=0. Так как для любого момента времени события нахождения элемента в одном из своих возможных состояний составляют полную группу, то выполняется нормировочное условие

P₁(t) + P₂(t) = 1 (7)

Интенсивности уравнения (7) можно представить в виде квадратной матрицы 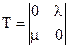, имеющей однозначное соответствие с марковским графом.

В матричном виде (6) можно записать как

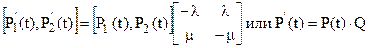. (7)

Здесь P¢(t), P(t) – вектор строки, Q – инфинитезимальная матрица. Между элементами матриц T и Q имеется очевидная связь: .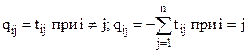

Если мы будем строить марковские модели надежности систем, состоящих из нескольких элементов, а возможно и учитывать некоторые внешние факторы, то очевидно, что пространство состояний модели будет увеличиваться. Система дифференциальных уравнений относительно P_i(t) (i = 1, 2, …, n) в общем виде записывается как

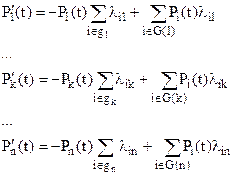, (8)

где g_k – множество состояний, в которые возможен непосредственный переход из данного состояния k; G(k) – множество состояний, из которых возможен непосредственный переход в состояние k.

Уравнения вида (8) для вероятностей состояний марковского процесса с непрерывным временем и дискретным множеством состояний называются уравнениями Колмогорова-Чепмена.

Произведение P_i(t)λ_ij имеет название потока вероятности. При составлении уравнений Коломогорова-Чепмена по графу переходов удобно пользоваться следующим правилом: производная вероятности любого состояния равна сумме потоков вероятности, переводящих систему в это состояние, минус сумме всех потоков вероятности, выводящих систему из этого состояния.

III. Аналитические методы решения уравнений Колмогорова-Чепмена на примере восстанавливаемого элемента

Метод решения, основанный на преобразовании Лапласа.

Применим к системе дифференциальных уравнений (6), описывающих процесс отказов и восстановлений элемента, преобразование Лапласа. В результате получаем систему алгебраических уравнений

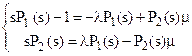, (9)

где 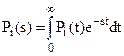- есть преобразование Лапласа для P_i(t).

Таблица преобразований Лапласа основных функций, используемых при расчетах надежности, приведена ниже.

Таблица 1. Формулы преобразований Лапласа.

Изображение	Оригинал	Изображение	Оригинал
αp₁(s)+βp₂(s)	αp₁(t)+βp₂(t)	1/s	1(t)
sp(s)-p(0)	p¢(t)	1/sⁿ,n=1,2…	t^n-1/(n-1)!
e-^bsp(s)	p(t-b)	1/(s-b)	e^bt
(1/b)p(s/b), b>0	p(bt)	1/(s-b)ⁿ,n=1,2…	(tⁿ^-1/(n-1)!)e^bt

Систему (9) удобно записать в виде

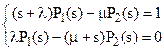(10)

Находим решение системы алгебраических уравнений (10), например, используя правило Крамера, и далее представляем его в виде суммы простых дробей для получения обратного преобразования Лапласа:

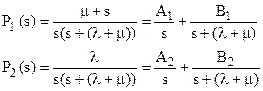(11)

Соотношения 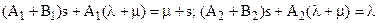позволяют найти искомые коэффициенты:

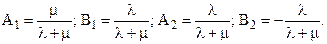(12)

Воспользовавшись формулами таблицы 1, находим P₁(t) и P₂(t) как обратное преобразование Лапласа от P₁(s) и P₂(s):

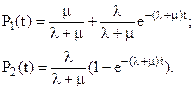(13)

Вероятность P₁(t) есть вероятность застать восстанавливаемый элемент в работоспособном состоянии в произвольный момент времени t. Эта вероятность является одним из важнейших показателей надежности восстанавливаемых систем и называется коэффициентом готовности К_Г(t).

Вероятность P₂(t) есть вероятность застать восстанавливаемый элемент в неработоспособном состоянии в произвольный момент времени t. Этот показатель называется коэффициентом простоя К_П(t).

Метод решения, основанный на сведении системы n уравнений к уравнению n-го порядка

Выразим из второго уравнения системы (6) неизвестную вероятность P₁(t)

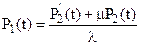. (14)

Подставив полученное выражение в первое уравнение системы (6), получим линейное однородное дифференциальное уравнение второго порядка:

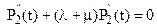. (15)

Характеристическое уравнение для (15) имеет вид

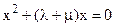. (16)

Корни характеристического уравнения равны: .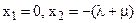

Корню x₁=0 соответствует решение С₁e^x₁^t=C₁. Корню x₂=-(λ+m) соответствует решение

С₂e^x₂^t=C₂.e^-(λ⁺^m^)t_.

Общее решение однородного уравнения (16) имеет вид:

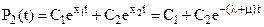(17)

Найдем значение произвольных постоянных С₁ и С₂. Для этого подставим в общее решение начальное условие P₂(0)=0. Тогда С₁ = - С₂. Выразим (14) через общее решение и, учитывая начальное условие P₁(0)=1, получим

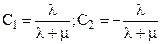. (18)

Рассмотренные два метода не являются единственными методами аналитического решения систем дифференциальных уравнений, описывающих динамику вероятностей пребывания системы в множестве ее возможных “надежностных” состояний. Например, известные методы, основанные на вычислении собственных значений и собственных векторов. В заключении отметим, что все аналитические методы явным или неявным образом связаны с решением характеристического уравнения, которое для систем большой размерности не решается аналитически. Поэтому в современном программном обеспечении анализа надежности на марковских моделях решение уравнений Колмогорова-Чепмена реализуется численными методами. Так как марковские модели надежности в виду большой разницы в значениях интенсивностей отказов (λ≈10^-6÷10^-9) и интенсивностей восстановлений (m≈1÷100) порождают жесткие дифференциальные уравнения, то пользуются специальными численными методами. Создание эффективных методов для решения жестких уравнений является областью активных математических исследований. Обсуждение этих методов выходит за рамки данного курса, а интересующимся читателям можно предложить книгу Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М: Мир, 1999.

IV. Расчет показателей безотказности восстанавливаемых систем на Марковских моделях.

1. Расчет вероятности безотказной работы.

Для восстанавливаемых систем при нахождении показателя вероятности безотказной работы необходимо все состояния отказа сделать поглощающими.Формально это означает удаление всех ветвей марковского графа (или обнуление интенсивностей перехода), соответствующих возврату из отказовых состояний в работоспособные. После этого для каждого k-го состояния работоспособности системы можно записать следующее дифференциальное уравнение:

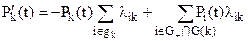, (19)

где G₊ - множество состояний работоспособности системы.

Для случая восстанавливаемого элемента марковский граф с поглощающим состоянием отказа имеет вид, показанный на рис.2.

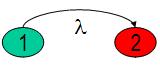
Рис. Марковский граф с поглощающим состоянием отказа.

Тогда вероятностью безотказной работы будет P₁(t), которая определяется из решения уравнения:

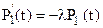. (20)

Начальное условие: P₁(0)=1.

Разделяя переменные и интегрируя левую и правую части, получаем известное выражение для вероятности безотказной работы экспоненциально распределенного элемента (P(t)):

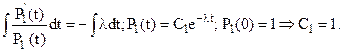
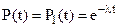(21)

2. Расчет средней наработки до отказа

Известно, что средняя наработка до отказа (Т) и вероятность безотказной работы связаны соотношением 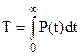. Следовательно, показатель средней наработки до отказа можно получить, интегрируя систему дифференциальных уравнений для модели с “поглощением”. Рассмотрим общий случай системы с n состояниями, в которой n-ое состояние является поглощающим (отказ системы):

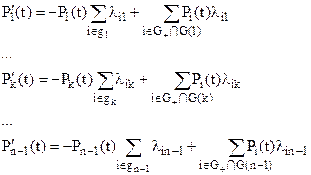(22)

Начальные условия: P₁(0)=1, …P_k(0)=0,…P_n(0)=0.

Проинтегрируем левые и правые части уравнений (22). Учитывая, что при наличии поглощающего состояния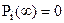, имеем

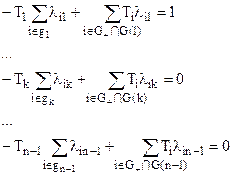, (23)

где T_i – среднее время пребывания в работоспособном состоянии i при начале работы из исправного состояния.

Средняя наработка до отказа Т определяется суммированием T_i по всем работоспособным состояниям:

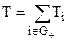(24)

Для одного элемента, c учетом P₁(0)=1, имеем: -1=-λT, откуда

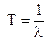(25)

V. Расчет стационарных показателей на Марковских моделях надежности

В теории случайных процессов доказано, что однородный марковский процесс без поглощающих состояний (состояний, из которых нет выхода) имеет стационарный режим, который обязательно наступит при достаточно больших временах (t→∞). Стационарный режим характеризуется тем, что вероятности P_i уже не зависят от времени, а, следовательно, их производные становятся равными нулю. Поэтому для вычисления стационарных вероятностей состояний системы необходимо приравнять к нулю производные, стоящие в левых частях уравнений (8). Чтобы полученная система не была вырожденной, одно из уравнений заменяют на условие нормировки (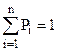). В результате получаем следующую систему n алгебраических уравнений для определения стационарных показателей надежности:

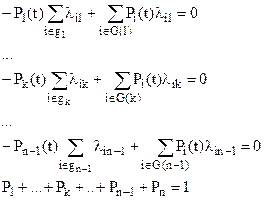(26)

Решение системы (26) позволяет получить такие показатели надежности как стационарный коэффициент готовности К_Г (вероятность застать объект в работоспособном состоянии в произвольный, достаточно удаленный момент времени) и стационарный коэффициент простоя К_П (вероятность застать объект в неработоспособном состоянии в произвольный, достаточно удаленный момент времени).

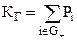, (27)

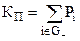, (28)

где G_- - множество всех неработоспособных состояний системы.

Проведем исследование надежности системы из одного восстанавливаемого элемента (рис.1) на стационарном участке. Система алгебраических уравнений, полученных из (6) при t→∞, имеет вид

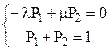. (29)

Решение системы: .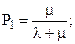

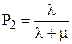Полученные на марковской модели показатели надежности восстанавливаемого элемента сведены в таблицу 2.

Таблица 2. Формулы показателей надежности восстанавливаемого элемента.

Коэффициент готовности: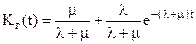
Коэффициент простоя: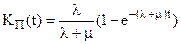
Стационарный коэффициент готовности: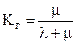
Стационарный коэффициент простоя: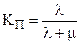
Вероятность безотказной работы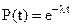
Средняя наработка до отказа: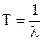

Литература к лекции 7.

Пугачев В.С. Введение в теорию вероятностей. М.: Наука, 1968.
Вентцель Е.С. Теория вероятностей. М.: Наука, 1969.
Дружинин Г.В. Надежность автоматизированных производственных систем. М.: Энергоатомиздат, 1986.
Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М.: Наука, 1991.
В.А. Острейковский. Теория надежности. М.: “Высшая Школа”, 2003.

Лекция 8. Укрупнение состояний марковской модели.

Аналитические марковской модели являются мощным и достаточно универсальным математическим аппаратом анализа надежности сложных систем. Однако при их применении возникают известные проблемы размерности – рост пространства состояний модели и связей между состояниями при увеличении количества элементов анализируемой системы. В общем случае размерность пространства состояний марковской модели ³ 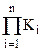, где n – количество элементов системы, K_i – количество состояний, в которых может находиться i-й элемент системы, например, устройство контроля может находится в трех состояниях (работоспособном и состояниях, соответствующих двум вида неработоспособности: отказа типа несрабатывания, отказа типа ложное срабатывание). Если элемент может находиться в двух состояниях, работоспособном и неработоспособном, то размерность марковской модели будет ³ 2ⁿ.

Сравним с точки зрения размерности три модели надежности: блок-схему, дерево отказов, марковской граф для системы из трех разнонадежных параллельно работающих элементов, отказом, которой является отказ всех трех ее элементов (критерий работоспособности “1 из 3”). На рис. 1 а,б,в показаны три разные модели надежности этой системы – марковской граф, блок-схема,. Очевидно, что в данном случае логико-вероятностные модели оказываются гораздо более компактными, чем марковской. Если к тому же учесть, что для расчета показателей надежности на марковской модели необходимо составить и решить систему дифференциальных уравнений, а расчет на блок-схемах и деревьях сведется в данном случае к достаточно простому преобразованию логических функций и замене логических переменных вероятностными, то сравнение будет не в пользу марковской модели. Однако это не так:

Как только мы захотим снять предположение о полной независимости процесса восстановления элементов (модели рис.1. построены именно при этом предположении), то логико-вероятностные методы перестают “работать”. На марковской модели мы можем учесть ряд особенностей процесса восстановления (ограничение на число ремонтных бригад, приоритеты, останов системы при ремонте и пр.). Логико-вероятностные модели описывают только случай неограниченного, независимого восстановления элементов, причем восстановление производится при работающей системе, что очень редко выполняется на практике.
Для систем с восстановлением на логико-вероятностных моделях рассчитываются лишь точечные показатели надежности, определяемые в момент времени t, например, коэффициент готовности, коэффициент простоя. Марковские модели позволяют вычислять все основные показатели надежности, как точечные, так и интервальные, например, вероятность безотказной работы (отказа) на интервале времени (0,t), средняя наработка до отказа.
Вычислительные мощности современных компьютеров позволяют находить численное решение систем дифференциальных и алгебраических уравнений большой размерности, порождаемых марковской графами..

Все же проблема размерности Марковских моделей решена быть полностью не может. Актуальной является эргономическая часть проблемы, связанная с трудностью входного описания модели и определения ее параметров человеком. Построение марковского графа с тысячью вершин является чрезвычайно трудной задачей для человека.. Поэтому при построении Марковских моделей обычно не рассматривают все множество возможных состояний системы, а стараются или удалить некоторые состояния, исходя из условий функционирования системы, и/или укрупнить (объединить) некоторые группы состояний в одно.

Данная лекция будет посвящена изучению формальных правил укрупнения состояний марковской модели.

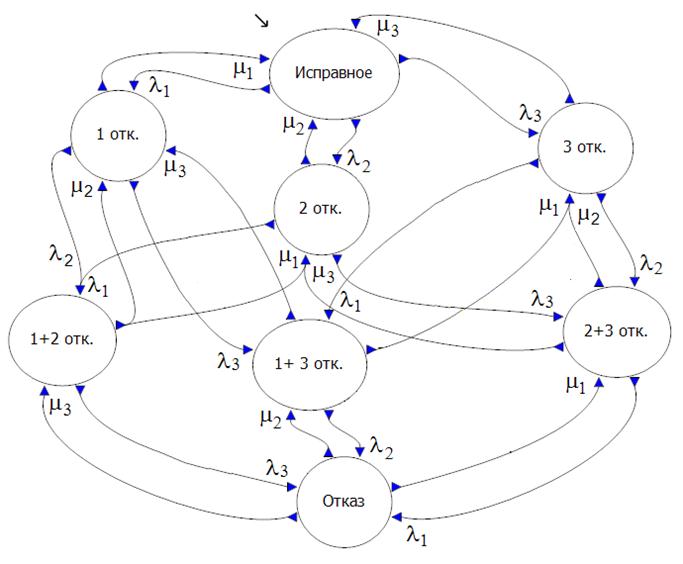
а). марковской модель.

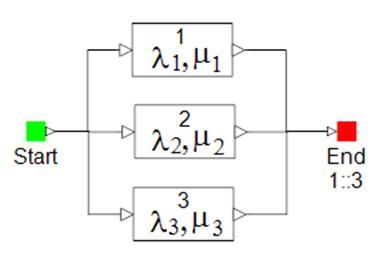
б). блок-схема надежности

Рис.1. Модели надежности системы “1 из 3” из разнонадежных элементов.

I. Марковская модель надежности восстанавливаемой дублированной системы.

Укрупнение состояний арковской процесса может быть точным или приближенным. Исследуем условия реализации точного укрупнения и продемонстрируем технику объединения состояний на конкретном примере. Построим арковской модель надежности дублированной системы из разнонадежных элементов с интенсивностью отказов λ₁, λ₂ и интенсивностью восстановления m₁, m₂ соответственно (рис.2). Здесь 0 –исправное состояние, 1 и 2 – работоспособные состояния одиночного отказа, 3 – отказ системы.

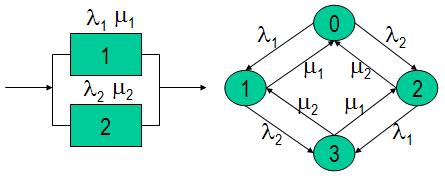
Рис.2. Марковский граф дублированной системы из разнонадежных элементов.

Система дифференциальных уравнений относительно состояний арковской процесса имеет вид

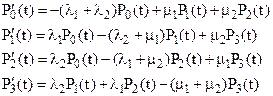. (1)

Начальные условия: P₀(0)=1; P₁(0)=P₂(0)=P₃(0)=0.

Прямое преобразование Лапласа от системы дифференциальных уравнений (1):

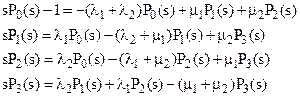(2)

Корни характеристического уравнения | Q-sE | =0, где Q – инфинитезимальная матрица, E- единичная матрица, равны:S₁= 0; S₂= - (l₁+m₁); S₃= - (l₂+m₂); S₄= - (l₁+m₁+l₂+m₂). Обозначим b=l₁+m₁, g=l₂+m₂, тогда S₁= 0; S₂= - b; S₃= - g; S₄= - (b +g).

Далее, разлагая выражения для Pi(s)на простые дроби и обращая их по стандартным формулам обратного преобразования Лапласа (см. лекцию 10), получаем ответ:

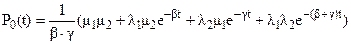
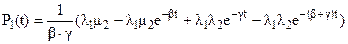(3)

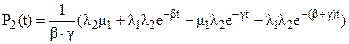
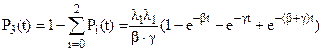
Из (3) получаем выражение для нестационарного коэффициента готовности дублированной системы с двумя разными элементами:

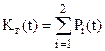(4)

Стационарные вероятности состояний равны:

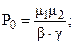
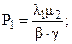
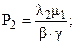
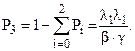(5)

Стационарный коэффициент готовности системы:

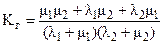(6)

Попробуем сократить пространство состояний модели, объединив два состояния 1 и 2 в одно. Это будет соответствовать ситуации, когда один элемент работает, а другой отказал и восстанавливается, то есть мы не будем различать какой из элементов работает, а какой отказал (рис.3). Но если интенсивности отказов и восстановлений каждого элемента разные, то свойство марковости будет при таком укрупнении нарушено! Если в обобщенное (укрупненное) состояние переход происходит при отказе элемента 1, то выход будет связан с отказом элемента 2 или с восстановлением элемента 1. В случае попадания в него при отказе элемента 2 – все наоборот. Для арковской же процесса неважно как система попадает в состояние, из которого в данный момент стартует! Налицо нарушение свойства отсутствия последействия – имеет значение прошлое и точно написать интенсивности выхода из укрупненного состояния нельзя. В этом случае можно построить приближенную укрупненную модель, показанную на рис.4. Эквивалентные интенсивности переходов λ_эи m_э приближенной модели рассчитываются по формулам

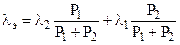(7)

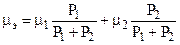(8)

Здесь P₁ и P₂ рассчитываются по формулам (5), 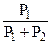- есть стационарная условная вероятность отказа первого элемента при условии, что откажет либо первый, либо второй, 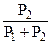- стационарная условная вероятность отказа второго элемента при условии, что откажет либо первый, либо второй. Точность приближения исходного (неукрупненного) процесса укрупненному зависит от соотношения интенсивностей отказов и восстановления. Чем большая разница между λ_i и m_I, тем точнее приближение.

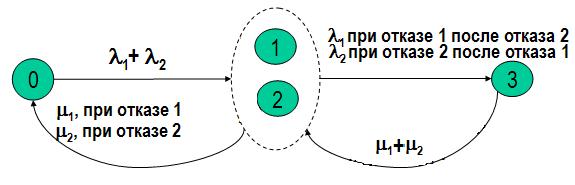
Рис.3. Попытка укрупнения состояний однократного отказа арковской модели дублированной системы из разных элементов.

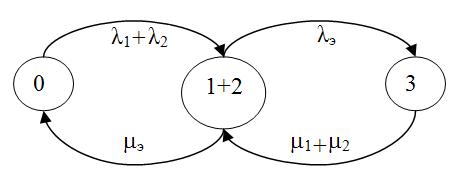
Рис.4. Приближенное укрупнение состояний однократного отказа арковской модели дублированной системы из разных элементов.

В подавляющем большинстве случаев резервированные системы формируются из одинаковых элементов. Рассмотрим дублированную систему с равнонадежными элементами (λ₁ = λ₂ и m₁ = m₂). Для модели этой системы (рис.5) интенсивности выхода из укрупненного состояния одинаковы и не зависят от того, каким образом мы в него попали. В этом случае укрупнение корректно и не нарушает свойство марковости.

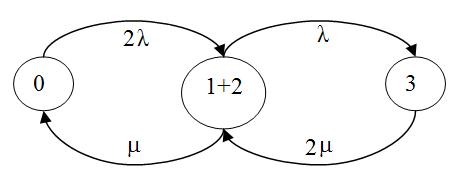
Рис.5. Точное укрупнение состояний однократного отказа арковской модели дублированной системы из одинаковых элементов.

Итак, точное укрупнение состояний арковской модели можно проводить при выполнении следующих условий:

1. Переходы из каждого из укрупняемых состояний возможны лишь в одни и те же состояния, т.е., если из одного из состояний, укрупняемых в одно, есть переходы в некоторое подмножество других состояний, то из других состояний, укрупняемых в одно, должны быть переходы в это же подмножество состояний.

2. Интенсивности выхода из состояний, укрупняемых в одно, должны быть одинаковыми

При соблюдении условий 1 и 2 необходимо руководствоваться следующими правилами:

Интенсивность перехода в укрупненное состояние равна сумме интенсивностей переходов в каждое из укрупняемых состояний.
Интенсивности выхода из укрупненного состояния равны интенсивностям выхода из одного из укрупняемых состояний.

II. Марковская модель надежности восстанавливаемой дублированной системы с облегченным резервом.

В соответствии с перечисленными правилами проведем укрупнение состояний арковской модели дублированной восстанавливаемой системы с резервным элементом, работающим в облегченном режиме (рис.6). Интенсивность отказов облегченного резерва = al (0£a£1).

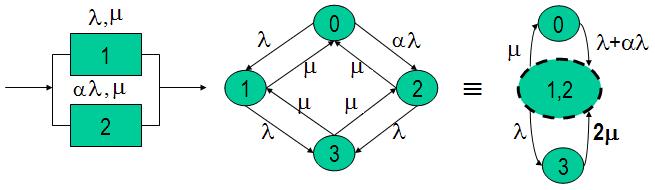
Рис.6. Марковская модель дублированной системы с облегченным резервом.

Система дифференциальных уравнений:

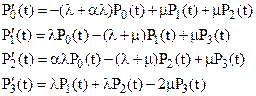(9)

В этой модели можно укрупнить состояния 1 и 2. Система дифференциальных уравнений после укрупнения имеет вид

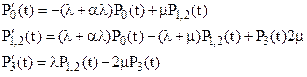(10)

Отметим, что система (10) могла быть получена формально в результате сложения уравнений относительно состояний 1 и 2 (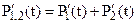). Система (10) полностью идентична (9) (в смысле одинаковости решений и определения всех показателей надежности), что подтверждает полную идентичность исходного и укрупненного графов переходов (рис.6).

III. Марковская модель надежности восстанавливаемой системы с гибридным резервированием и ограничением на число ремонтных бригад.

Достаточно часто повышение надежности обеспечивается комбинацией нагруженного и ненагруженного резерва. В этом случае говорят, что в системе реализовано гибридное резервирование. Построим арковской модель надежности системы с гибридным резервом, в которой имеется рабочий блок, состоящий из трех одинаковых параллельно работающих элементов. Кроме того, имеется два ненагруженных резервных элемента, подключаемых на место отказавших элементов рабочего блока (рис.7). Восстановление работоспособности отказавших элементов осуществляется двумя ремонтными бригадами. После попадания в отказовое состояние запуск системы в работу осуществляется только после того, как будет полностью восстановлен рабочий блок (отремонтированы все три элемента).

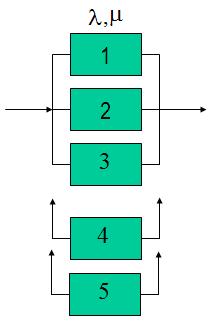
Рис. 7. Система с гибридным резервированием

Марковский граф системы показан на рис.8. Каждому состоянию (вершине графа) приписан код – N,K,W, где N – количество работоспособных элементов рабочего блока, K – количество работоспособных ненагруженных резервных элементов, W – количество элементов, ожидающих ремонта. Буква G означает исправное состояние, буква F – отказ.

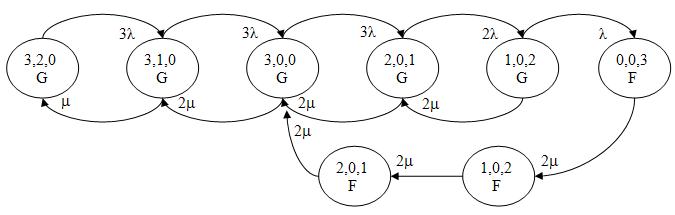
Рис.8. Марковский граф системы с гибридным резервированием.

В построенной арковской модели учтены следующие особенности:

· ненагруженное резервирование

· ограничение на число ремонтных бригад

· специальная стратегия восстановления системы

Ни одна из перечисленных особенностей не могла бы быть учтена в логико-вероятностных моделях. За счет укрупнения состояний одинаковой кратности отказов рабочего блока размерность модели снижена.

Литература к лекции 8.

1. Надежность технических систем: Справочник / Ю.К. Беляев, В.А.Богатырев, В.В. Болотин и др.; под ред. И.А.Ушакова. М.: Радио и связь, 1985.

2. Дружинин Г.В. Надежность автоматизированных производственных систем. М.: Энергоатомиздат, 1986.

3. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. М.: Наука, 1991.

4. Черкесов Г.Н. Надежность аппаратно-программных комплексов/Учебное пособие. – СПб,: “Питер”, 2005.

5. Половко А.М., Гуров С.М. Основы теории надежности. BHV- Санкт-Петербург, 2006.

Лекция 9. Исследование надежности сложных, восстанавливаемых систем на Марковских моделях.

Продолжим исследовать надежность систем, для корректного моделирования которых необходимо применять марковские процессы. Рассмотрим три примера

· расчет коэффициента готовности системы с зависимым функционированием элементов

· построение модели надежности системы с встроенным контролем и восстановлением, отложенным до окончания выполнения задания

· расчет стационарных показателей параметра потока отказов и среднего времени работы между отказами для резервированных структур с восстановлением элементов

I. Последовательная, восстанавливаемая система с зависимым функционированием элементов.

Рассмотрим систему, состоящую из n последовательно в смысле надежности соединенных элементов. Пусть при отказе любого одного элемента система отключается, т.е. функционирование прекращается для восстановления этого элемента. Это самое обычное условие эксплуатации. Например, телевизор состоит из модулей питания, строчной развертки, кадровой развертки, блока цвета, усилителя звука, высокочастотного усилителя сигнала….Отказ любого из модулей приводит к отказу телевизора, а для восстановления (ремонта) надо обязательно телевизор выключить. Это означает, что во время ремонта отказавшего модуля отказы других модулей или невозможны или их вероятностью можно пренебречь! Тогда число состояний марковской модели системы будет равно n+1, а не 2ⁿ(рис.1)^..

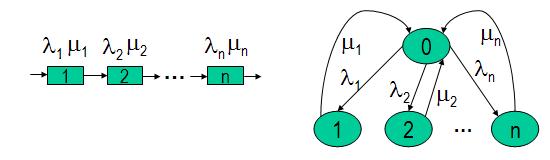
Рис.1. Марковская модель системы с зависимым функционированием элементов.

Выражение для стационарного коэффициента готовности находится из системы уравнений:

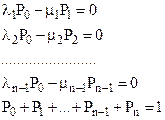. (1)

Решая(1),получаем

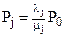. (2)

(2) позволяет выразить стационарную вероятность отказа i-го элемента (i=1, 2,…n) через вероятность исправного состояния P₀.

Подставив (2) в последнее уравнение системы (1), получаем выражение для стационарного коэффициента готовности системы

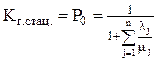(3)

Выразим стационарный коэффициент готовности системы K_г.стац.через коэффициенты готовности ее элементов K_j, где 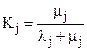. Тогда 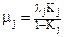, откуда получаем

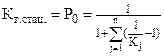(4)

Пусть n=3 K₁=0,61, K₂=0,72, K₃=0,63. Тогда из (4) K_г.стац.=0,38

Обычная ошибка состоит в вычислении коэффициента готовности такой системы умножением коэффициентов готовности элементов, т.е К_г.стац. = K₁ K₂ K₃ = 0,28, что дает неверный результат. Это объясняется тем, что перемножать коэффициенты готовности элементов для получения оценки показателя готовности системы можно лишь при независимости элементов! В данном случае имеется зависимость - при отказе одного из элементов другие не отказывают. Рассчитывать надо по (4)!

II. Система с встроенным контролем и восстановлением, отложенным до окончания выполнения задания.

Оперативный встроенный контроль (BIT – built-in-test) технического состояния элементов и систем, контроль правильности выполнения функций позволяет в полной мере реализовать возможности резервирования, своевременно принимать меры по реконфигурации систем и изменению режимов функционирования, обеспечивая, тем самым, свойство отказобезопасности системы в целом. Однако контроль не является идеальным – во-первых, он сам отказывает, а, во-вторых, не абсолютно все отказы им распознаются. Поэтому для обеспечения высоких показателей надежности и безопасности требуется проведение тщательного «надежностного» анализа систем с учетом характеристик контроля. Одной из важнейших таких характеристик является полнота контроля, характеризующая долю отказов объекта контроля, обнаруживаемых при контроле работоспособности. В общем случае качество контроля определяется перечнем элементов (модулей), отказы которых выявляются контролем. Поэтому одной из характеристик полноты контроля может быть отношение числа контролируемых элементов к общему числу элементов рассматриваемого объекта контроля (например, в процентах). Однако для совместного моделирования «надежностного поведения» объекта и средств контроля желательно задавать полноту контроля как некоторый вероятностный показатель или как отношение характеристик надежности (отказа) контролируемых элементов ко всем элементам. Целесообразность такого задания объясняется тем, что при моделировании «надежностного поведения» анализируемого объекта можно будет «разбить» общий поток отказов на две составляющие – выявляемые контролем отказы и скрытые отказы. Полноту контроля в этом случае можно определить как условную вероятностью контролируемого отказа, при условии, что отказ произошел:

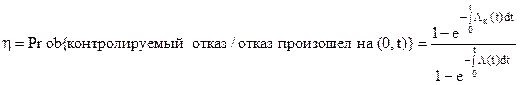’ (5)

где L – суммарная интенсивность отказов объекта контроля (контролируемые + неконтролируемые); L_к- суммарная интенсивность контролируемых отказов.

Проведя усреднение интенсивностей отказов на интервале (0,t), получаем:

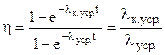’ (6)

где 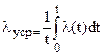и для реальных высоконадежных систем l_усрt << 1.

Общие выражения (5, 6) для полноты контроля при экспоненциальных распределениях наработки до отказа элементов наиболее удобно задавать как отношение суммарной интенсивности отказов контролируемых элементов к суммарной интенсивности отказов всех элементов, т.е.

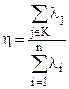, (7)

где h - полнота контроля; n –количество элементов объекта контроля; К - подмножество контролируемых элементов; λ_i – интенсивность отказа элемента. В этом случае определяемая полнота является условной стационарной вероятностью контролируемого отказа, при условии, что отказ произошел.

Построим модель надежности дублированной системы с встроенным контролем и восстановлением. Средства контроля будем считать абсолютно надежными, а его качество будем оценивать показателем полноты согласно (7). Восстановление работоспособности элементов происходит лишь при возникновении отказов, выявляемых BIT. Тогда дублированная система может быть представлена как параллельное соединение двух каналов, каждый из которых состоит из контролируемой и восстанавливаемой и неконтролируемой и невосстанавливаемой частей (рис.2). Интенсивности отказов контролируемой и неконтролируемой частей равны hl и (1-h)l соответственно.

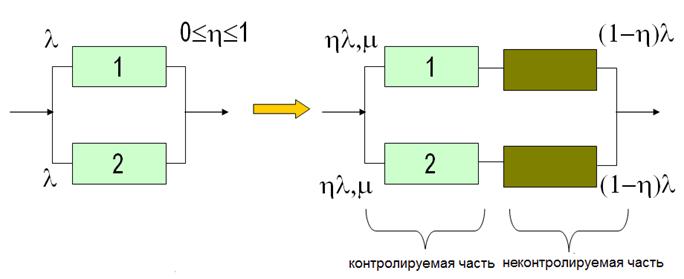
Рис.2. Дублированная система с восстановлением и неполным контролем

Отразим в модели циклический режим работы системы. Цикл состоит из выполнения задания и восстановительных работ, которые проводятся лишь после выполнения задания. Режим типичен для транспортных систем. Марковская модель надежности системы показана на рис.3.

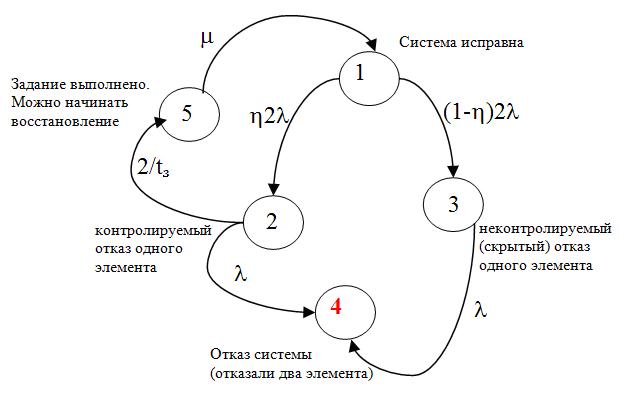
Рис.3. Марковская модель дублированной системы с восстановлением и неполным контролем. Циклический режим работы.

Для определения интенсивности перехода из состояния 2 в состояние 5 вычислим среднее время наступления отказа при условии, что отказ наступил на интервале времени выполнения задания (0,tз) T_ср/t_з:

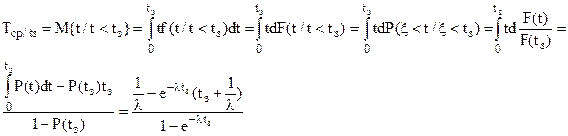, (8)

где M{t}, F(t), f(t) – есть соответственно математическое ожидание, функция распределения и плотность распределения случайного времени возникновения отказа.

Для значений интенсивности отказа l = 1e-3 на рис. 4 построен график, демонстрирующий тот факт, что если t_з << 1/l = T_c_р, то T_ср/t_з.» t_з/2. При t_з > T_c_р T_ср/t_з →T_ср. Поэтому для систем, время выполнения задания которых не превышает нескольких десятков часов, вполне корректным является допущение о том, что отказ происходит на середине интервала (0,t_з), а следовательно интенсивность перехода из 2 в 5 равна 2/t_з.

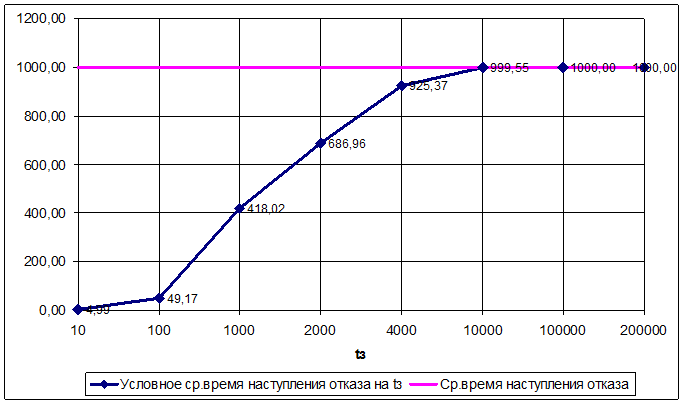
Рис.4. Условное среднее время возникновения отказа на интервале времени выполнения задания

III. Расчет стационарных показателей параметра потока отказов и среднего времени работы между отказами для резервированных схем с восстановлением элементов

Стационарный режим работы восстанавливаемой системы, моделируемой однородным марковским процессом без поглощающих состояний, может быть охарактеризован рядом специальных показателей. Два важнейших показателя - стационарный коэффициент готовности и стационарный коэффициент простоя были рассмотрены в V разделе 10 лекции. Здесь мы рассмотрим два других стационарных показателя – параметр потока отказов и средняя наработка между отказами и обсудим связь между этими показателями.

В марковских моделях надежности параметр потока отказов определяется из следующего выражения:

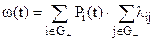. (9)

Для стационарного участка

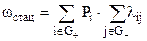, (10)

где G₊ - множество состояний работоспособности системы, G_- - множество состояний неработоспособности системы.

Параметр потока отказов является производной по времени от среднего числа отказов. Поэтому, зная параметр потока отказов, можно вычислить среднее число отказов на интервале времени (t₁,t₂):

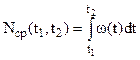(11)

Для стационарного участка

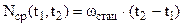(12)

Параметр потока отказов часто используется в моделях анализа безопасности, где необходимо оценить потери, связанные с переходами в состояния отказов.

Если рассматривать стационарный участок, то параметр потока отказов, характеризующий частоту возникновения событий отказа в восстанавливаемых системах, обратно пропорционален среднему времени между отказами (строгое доказательство этого положения приведено в теории восстановления). Поэтому

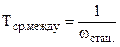(13)

Для обозначения показателя среднего времени между отказами в западной литературе используется аббревиатура MTBF (Mean Time Between Failures), которая в настоящее время стала применяться и отечественными специалистами. Здесь необходимо отметить, что в отечественной литературе присутствует показатель средней наработки между отказами (T_ср.) (рис.5). Связь между этими показателями следующая:

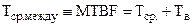, (14)

где T_в– среднее время восстановления.

Рис.5. Стационарный участок работы восстанавливаемой системы.

С учетом того, что 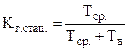и выражений (13, 14) получим

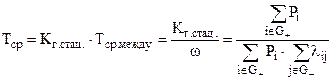. (15)

Для восстанавливаемого элемента параметр потока отказов равен

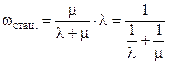(16)

Рассмотрим общую модель резервированных схем из идентичных элементов, показанную на рис.6. Модель пригодна для анализа надежности следующих схем:

дублированной схемы с нагруженным резервом
дублированной схемы с ненагруженным резервом
мажоритарной схемы

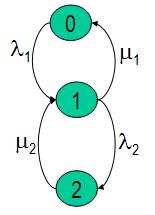
Рис.6. Общая модель резервированных схем.

Стационарные вероятности состояний определяются по формулам:

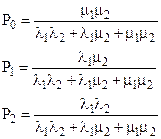(17)

Исходя из выражений (13)-(15) и учитывая, что 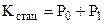, получены расчетные формулы для основных показателей надежности резервированных схем (см. таблицу 1). Вывод формул для показателя средней наработки до отказа осуществлялся методом, описанным в лекция 10 (23,24).

Таблица 1. Основные показатели надежности резервированных схем.

Схема	Стратегия восстановления	Параметры модели	Стационарный коэффициент готовности	Параметр потока отказов	Средняя наработка между отказами	Среднее время работы до отказа
Дублированная схема с нагруженным резервом	Неограниченное восстановление (две бригады)	l₁ = 2l, l₂ = l, m₁ = m, m₂ = 2m.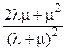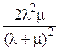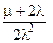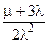
Дублированная схема с нагруженным резервом	Ограниченное восстановление (одна бригады)	l₁ = 2l, l₂ = l, m₁ = m, m₂ = m.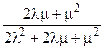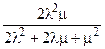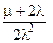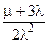
Дублированная схема с ненагруженным резервом	Неограниченное восстановление (две бригады)	l₁ = l, l₂ = l, m₁ = m, m₂ = 2m.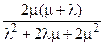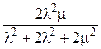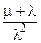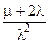
Мажоритарная структура “2 из 3”	Неограниченное восстановление (две бригады)	l₁ = 3l, l₂ = 2l, m₁ = m, m₂ = 2m.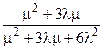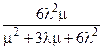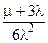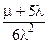

В таблице есть ошибки, о чем я Вам говорил!

Литература к лекции 9.

2. Дружинин Г.В. Надежность автоматизированных производственных систем. М.: Энергоатомиздат, 1986.

3. Ушаков И.А. Вероятностные модели надежности информационно-вычислительных систем. М.: Радио и Связь, 1991.

4. Кондратенков В.А., Котельников Г.Н., Мамченков В.Л. и др. Вопросы теории надежности технических систем. Смоленск, РУСИЧ, 1998.

5. Черкесов Г.Н. Надежность аппаратно-программных комплексов/Учебное пособие. - СПб,: “Питер”, 2005.

6. Половко А.М., Гуров С.М. Основы теории надежности. BHV- Санкт-Петербург, 2006.

Лекция 10. Исходные данные для расчетов надежности технических систем.

В предыдущих лекциях курса были рассмотрены модели и методы анализа надежности сложных технических систем с учетом резервирования, восстановления, характеристик средств встроенного контроля. Заключительная лекция курса будет посвящена обзору методов получения обоснованных исходных данных для работы с рассмотренными моделями надежности, включая:

· методы расчета интенсивностей отказов элементов по стандартизованным моделям

· методы расчета средних времен восстановления

· анализ видов и последствий отказов

I. Прогнозирование безотказности элементной базы

Вопросы расчета интенсивностей отказов (λ-характеристик) элементов технических систем решаются в специальном разделе теории надежности, называемом “прогнозирование безотказности”. Напомним, что интенсивность отказов λ(t) и вероятность безотказной работы P(t) связаны соотношением

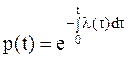, (1)

которое для экспоненциального распределения (l(τ)=l=const) преобразуется к виду .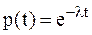

Предположение о постоянстве l-характеристик далеко не всегда справедливо и более правильно было бы использовать для описания случайных наработок до отказа элементов более общие законы, например, двухпараметрическое распределение Вейбулла. Однако, как это уже было продемонстрировано в предыдущих лекциях, экспоненциальное распределение широко используется т.к.:

· проведение расчетов надежности аналитическими методами возможно, в основном, толькодля экспоненциального распределения случайных наработок до отказа.

· определение параметров “стареющих” (“молодеющих”) многопараметрических распределений – сложная и трудоемкая задача.

В рамках прогнозирования безотказности решаются следующие задачи:

· создание моделей и определение расчетных соотношений для вычисления интенсивностей отказов элементов

· разработка методов корректировки расчетных интенсивностей по результатам испытаний и эксплуатации

· вычисление показателей безотказности последовательных систем

· создание, ведение, непрерывное периодическое обновление баз данных, хранящих статистически обработанную информацию по отказам элементной базы.

Модели, применяемые при расчете l-характеристик, ориентированы на определенную классификацию элементов. Согласно этой классификации все элементы и устройства делятся на классы электрические, электронные, механические, электро-механические. Каждый класс, в свою очередь, делится на категории и подкатегории. Например, у электронных компонентов есть категория – Интегральные Схемы, которая делится на подкатегории ОЗУ, микропроцессоры, программируемые логические матрицы, ППЗУ и пр., или категория Резисторы с подкатегориями – точные, переменные, проволочные, непроволочные, термо, пленочные…. В электромеханике есть категория Антенны с подкатегориями – радио, связь, микроволновые, радары, автомобильные и пр. У механических – Клапаны, делящиеся на подкатегории тарельчатые, игольчатые, шунты, задвижки, шаровые….

Принципы составления расчетных соотношений для определения l-характеристик следующие. Для каждого типа элемента с фиксированным значением категория/подкатегория, исходя из физики отказов и статистических данных, определяется т.н. базовая интенсивность (или интенсивности). Далее эти интенсивности корректируются набором коэффициентов (Pi Factors), значения которых вычисляются на основе задаваемых параметров (набор коэффициентов – уникален для данной категории/подкатегории). Коэффициенты могут учитывать: условия работы, качество изготовления и обслуживания, степень защиты, электрическую нагрузку, режимы (хранение, работа), температуру, технологию изготовления, конструкцию корпусов, степень интеграции, влияние вибраций и ударов, число включений/выключений.

Приведем примеры некоторых формул, с помощью которых определяются l-характеристики элементов заданной категории/подкатегории для электронного, механического, электромагнитного оборудования:

Пример 1. Интегральные схемы/Микропроцессоры.

Интенсивность отказов микропроцессоров рассчитывается по формуле

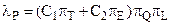, (2)

где C₁ – составляющая интенсивности, зависящая от сложности кристалла, p_T – температурный коэффициент, С₂ – интенсивность отказов корпуса, p_E – коэффициент окружающей среды (условий эксплуатации), p_Q – коэффициент качества, p_L – коэффициент приработки.

Наиболее существенное влияние на λ_р оказывает температура (рис.1).

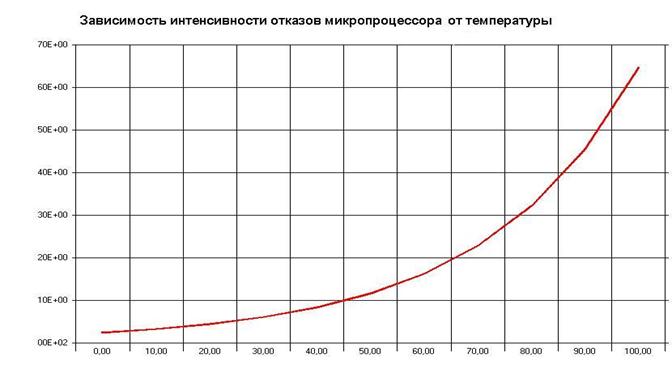
Рис.1. Зависимость интенсивности отказов микропроцессора (λ_р*10⁶) от температуры.

Пример 2. Трубопроводная арматура/Тарельчатый клапан.

l_PO = l_PO_,B(Q_a/Q_f), (3)

где l_PO_,B - базовая интенсивность отказов (1/млн.операций);

Q_a – интенсивность утечки (дюйм³/мин);

Q_f – допустимая по спецификациям интенсивность утечки (дюйм³/мин).

Q_a = (2*10⁴*D_MS*f³*(P₁²-P₂²))/(V_a*L_w*(S)^1.5), где D_MS – средний посадочный диаметр в дюймах; f – чистота поверхности в микродюймах; P₁,P₂ – давление до и после клапана в фунтах/кв.дюйм; V_a – абсолютная скорость жидкости ((фунт*мин)/кв.дюйм); L_w – ширина посадочного места (дюйм); S – посадочная нагрузка (фунт/кв.дюйм).

Пример 3. Индуктор/Трансформатор.

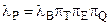, (4)

где l_B - базовая интенсивность отказов

При выполнении расчетов Pi коэффициенты и базовые интенсивности определяются из таблиц, приведенных в соответствующей нормативной литературе, с учетом спецификаций элементов и условий эксплуатации. Например, для определения С₂ (базовой интенсивности отказов корпуса микропроцессора) надо провести расчеты с использованием следующей таблицы:

Таблица 1. Базовая интенсивность отказов корпуса.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: