Необходимое условие экстремума

КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

ВЫСШАЯ МАТЕМАТИКА

ЧЕЛЯБИНСК

УДК 510(022)(075)

В152

Валеева З.С., Неупокоев В.А., Валеев Г.А.

Высшая математика. Учебное пособие. ЧИПС

Челябинск 2006.103с.

Пособие включает элементы линейной и векторной алгебры, аналитической геометрии и основы математического анализа (дифференцирование функций и их исследование), функцию нескольких переменных, неопределенные, определенные и несобственные интегралы, а также дифференциальные уравнения.

Предназначено для студентов очной, заочной форм обучения.

Рецензенты: В.Н. Ни, доктор физико - математических наук, профессор, академик РАЕН;

Г.В. Савельев, кандидат технических наук, профессор

Одобрено учебно – методическим советом Челябинского института путей

сообщения.

@ Филиал Уральского государственного университета путей сообщения.

Челябинский институт путей сообщения,2006

Введение

Курс «Высшая математика» является фундаментальным курсом необходимым как при изучении курсов математического цикла, так и при изучении специальных курсов основ железнодорожного транспорта, изучающих конкретные задачи прикладного характера, а также экономики, финансов и бизнеса.

Настоящее учебное пособие предназначено для студентов дневного, а также заочного обучения при их самостоятельном освоении курса “Высшая математика”.

Целью курса является формирование у студентов математического аппарата необходимого для решения теоретических и практических задач и умения самостоятельно изучать литературу по математическому анализу.

Задачи дисциплины:

1. Получение теоретических знаний по ряду разделов математики.

2. Практическое освоение приемов и методов решения математических задач, имеющих применение при рассмотрении вопросов в других дисциплинах учебного плана.

Краткая характеристика дисциплины

Курс включает элементы линейной и векторной алгебры, аналитической геометрии и основы математического анализа (дифференцирование функций и их исследование), функцию нескольких переменных, неопределенные, определенные и несобственные интегралы, а также дифференциальные уравнения.

Курс ориентирован на приобретение теоретических знаний и практических навыков в решении задач по математике.

Учебная программа по высшей математике ведется в форме лекций, практических занятий и самостоятельной работы студентов. Теоретические положения предмета даются на лекциях.

На практических занятиях студенты осваивают приемы решения задач. Каждое практическое занятие способствует развитию активного применения полученных на лекциях теоретических знаний. Это позволит эффективно закреплять теоретические знания и использовать их в практической работе и исследовательской деятельности студентов.

При изучении курса предусмотрена самостоятельная работа, которая включает: изучение основной и дополнительной литературы, учебных пособий, конспектов лекций и практических занятий, а также выполнение домашних заданий с решением примеров и задач по каждому разделу изучаемого курса.

Проверка знаний осуществляется в виде проверки выполнения домашних заданий, проведения контрольных работ, а также в ходе экзаменов, на которых определяется итоговый уровень знаний студентов по пройденным разделам курса.

Требования к экзаменам. К экзаменам допускаются студенты, отработавшие на практических занятиях или самостоятельно (для студентов заочного обучения) основные вопросы учебных тем программы и получившие положительные оценки по контрольным работам.

При подготовке к экзаменам студент должен:

1. Освоить основные понятия и определения линейной и векторной алгебры, аналитической геометрии и математического анализа; функции нескольких переменных, неопределенных, определенных и несобственных интегралов, а также дифференциальных уравнений

2. Научиться решать математические задачи по пройденным темам учебной программы и подтвердить свое умение самостоятельным их решением в присутствии преподавателя.

Студент должен знать:

1. Элементы линейной алгебры: линейные уравнения, системы линейных уравнений, матрицы и определители, их свойства и действия над ними, методы решения систем линейных уравнений.

2. Основные понятия векторной алгебры: векторы, проекции векторов на координатные оси, представления векторов в координатной форме, линейные операции над векторами геометрически и аналитически с помощью координат, скалярное и векторное произведения векторов и их свойства.

3. Основные понятия аналитической геометрии: координаты точек, координатная форма представления линий и поверхностей с помощью алгебраических уравнений, формы записи уравнений прямых линий и линий второго порядка на плоскости, а также уравнений прямой и плоскости в пространстве.

4. Основные понятия математического анализа: функция, аргумент, ее область определения, пределы функции в точке и на бесконечности, непрерывность функции, точки разрыва, производная функции, ее физический и геометрический смысл, основные правила дифференцирования, основные теоремы дифференциального исчисления, исследование функций и построение их графика.

5. Определение функции двух переменных. Понятие частных производных и способы нахождения локального экстремума и наибольшего значения функции двух переменных.

6. Определения первообразной, неопределенного, определенного и несобственного интегралов. Их основные свойства. Основные методы интегрирования: непосредственное интегрирование, метод подстановки или замены переменной, интегрирование по частям.

7. Формулу Ньютона-Лейбница. Геометрические и физические приложения определенного интеграла: вычисление площади плоской фигуры, определение работы переменной силы на прямолинейном отрезке.

8. Дифференциальные уравнения 1-го порядка. Задачу и теорему Коши о существовании и единственности решения дифференциальных уравнений.

9. Основные виды дифференциальных уравнений 1-го порядка: уравнения с разделяющимися переменными, однородные и линейные уравнения.

10. Дифференциальные уравнения 2-го порядка, его общее и частное решения. Дифференциальные уравнения, допускающие понижения порядка. Линейные дифференциальные уравнения 2-го порядка.

Студент должен уметь:

1. Вычислять определители матриц, выполнять различные действия с матрицами, решать системы линейных уравнений методами Крамера, Гаусса и матричным методом с помощью обратных матриц.

2. Выполнять линейные операции над векторами (находить сумму, разность векторов, произведение вектора на скаляр) как геометрическим построением, так и аналитически с помощью их координат, находить скалярное и векторное произведения векторов.

3. Составлять уравнения прямых линий и преобразовывать эти уравнения из одного вида в другой; находить точки пересечения линий, заданных уравнениями; определять параллельность и перпендикулярность прямых, а также находить угол между ними. Строить линии второго порядка – окружность, эллипс, параболу, гиперболу. Составлять уравнения прямых линий и плоскости в пространстве и строить их в прямоугольной системе координат.

4. Находить пределы функций в точке и на бесконечности. Вычислять производные различных функций; проводить исследование функций и строить их графики.

5. Выполнять дифференцирование функции двух переменных - находить частные производные и определять локальные экстремумы этих функций.

6. Вычислять неопределенные, определенные и несобственные интегралы. Решать геометрические и физические задачи по вычислению площади плоских фигур и определению работы переменной силы на прямолинейном отрезке.

7. Находить общее и частное решения основных видов дифференциальных уравнений 1-го порядка (уравнений с разделяющимися переменными, однородных и линейных уравнений), а также дифференциальных уравнений 2-го порядка (уравнений, допускающих понижения порядка, и линейных уравнений).

1. Элементы линейной алгебры

1.1. Решение системы линейных уравнений с двумя неизвестными методом Крамера

Система линейных уравнений с двумя неизвестными имеет вид:

(1),

где x, у - неизвестные, а_i,j - коэффициенты при неизвестных х,у; индексы: i=1,2 - определяет номер уравнения, j=1,2 - определяет номер неизвестного; b₁, b₂ - свободные члены уравнения.

Дадим ряд определений.

Определение: Решением системы линейных уравнений (1) называется пара чисел (х₀,у₀), при подстановке которой в эту систему все уравнения обращаются в верные числовые тождества.

Определение: Система уравнений называется совместной, если она имеет хотя бы одно решение. Система называется несовместной, если она не имеет решений.

Определение: Совместная система уравнений называется определенной, если она имеет единственное решение. Совместная система называется неопределенной, если она имеет несколько решений.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ

Геометрически система уравнений с двумя неизвестными задает две прямые на плоскости.

При этом возможны 3 случая:

1) прямые пересекаются в одной, единственной точке – в этом случае система имеет единственное решение, она совместна и определена;

2) прямые совпадают, имеется бесконечное множество совместных точек - в этом случае система совместна, но не определена;

3) прямые параллельны и общих точек пересечения нет - в этом случае система несовместна и решений не имеет.

Введем понятие матрицы и определителя второго порядка.

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ ВТОРОГО ПОРЯДКА

Определение: Квадратной матрицей 2-го порядка называется таблица чисел, которая состоит из 2-х строк и 2-х столбцов и обозначается:

А = ,

где а_i,j - называются элементами матрицы, индексы: i = 1, 2 - определяет номер строки, j = 1, 2 - номер столбца.

Элементы а₁₁а₂₂ образуют главную диагональ матрицы, а элементы а₁₂а₂₁ образуют побочную диагональ матрицы.

Каждая матрица характеризуется своим определителем.

Определение: Определителем матрицы 2-го порядка называется число, которое определяется по методу диагоналей - как разность произведений элементов главной и побочной диагоналей.

Определитель 2-го порядка обозначается и вычисляется по следующей схеме: .

Пример. Вычислить определитель матрицы A =

Решение: 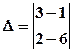= 3(-6) - (-1) 2 = -16.

ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ

1.Определитель не изменится, если его строки и столбцы поменять местами: .

2. При перестановке двух строк или столбцов определитель меняет знак на противоположный: .

3. Определитель с двумя одинаковыми строками или столбцами равен нулю:

.

4. Определитель равен нулю, если все элементы какой-нибудь строки или столбца равны нулю: .

5.Общий множитель всех элементов строки или столбца можно вынести за знак определителя: .

6. Если строка или столбец определителя состоит из двух слагаемых или разности, то определитель можно разложить на два определителя:

.

7. Определитель не изменится, если к элементам любой строки или столбца прибавить или отнять соответствующие элементы другой строки или

столбца, умноженные на одно и тоже число: .

Рассмотренные выше свойства определителей 2-го порядка распространяются на определители более высокого порядка.

Перейдем к решению системы линейных уравнений с двумя неизвестными методом Крамера.

Систему (1) путем последовательного исключения неизвестных х и у приведем к равносильной (эквивалентной) системе (2), имеющей одинаковые решения с исходной системой (1).

Действительно, если умножить 1-е уравнение системы (1) на коэффициент а₂₂, а 2-е уравнение на коэффициент а₁₂ и вычтем из 1-го, исключим тем самым неизвестную у. Аналогичным образом исключив из уравнений неизвестную х, получим равносильную системы (2): (2)

Перепишем эту систему через определители 2-го порядка в виде:

(2),

где - называется определителем системы;

- называется определителем неизвестного х;

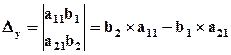- называется определителем неизвестного у.

Определители неизвестных получаются из определителя системы путем замены столбца коэффициентов при неизвестном на столбец свободных членов.

При решении системы (2) возможны 3 случая при выполнении следующих условий:

1. Если определитель системы (2) , то, поделив обе части уравнений системы на , получим единственное решение, которое находится по формулам Крамера: .

При первом условии система имеет единственное решение, она совместна и определена. Прямые пересекаются в одной точке с координатами М(х_0, у₀).

2. Если определитель системы и определители неизвестных также = 0, то система (2) имеет вид: и при любых значениях х и у имеем верные числовые тождества.

При втором условии система имеет бесконечное множество решений, она совместна, но не определена. Прямые совпадают друг с другом.

3. Если определитель системы , а хотя бы один из определителей неизвестных или или , то система (2) имеет вид: , что невозможно при любых значениях х и у.

При третьем условии система решения не имеет, она не совместна. Прямые параллельны друг другу и общих точек пересечения не имеют.

Метод решения системы линейных уравнений с помощью определителей называется методом Крамера.

Пример. Решить систему линейных уравнений методом Крамера:

Решение: 1) Вычислим определители системы и неизвестных D, D_х и D_у.

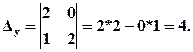
2) Найдем решение системы по формулам Крамера:

х₀ ; у₀ =

Проверка: (верно).

Ответ: (х₀=6, у₀=4) –координаты точки пересечения прямых.

1.2. Решение системы линейных уравнений с тремя неизвестными методом Крамера

Система трех линейных уравнений с тремя неизвестными имеет вид:

(3),

где a_ij - коэффициенты при неизвестных х, у и z, индексы: i = 1,2,3 - определяют номер уравнения и j = 1,2,3 - номер неизвестного.

Определение: Решением системы уравнений (3) называется тройка чисел (х₀,у₀,z₀), при подстановке которой в эту систему все уравнения обращаются в верные числовые тождества.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ РЕШЕНИЯ СИСТЕМЫ уравнений с тремя неизвестными

Геометрически система уравнений (3) задает 3 плоскости в пространстве.

При этом возможны 3 случая:

1) плоскости пересекаются в единой точке с координатами (x_0,y_0,z₀), система в этом случае имеет единственное решение - она совместна и определена;

2) плоскости совпадают друг с другом - система имеет бесконечное множество решений, т.е. она совместна, но не определена;

3) плоскости параллельны друг другу и общих точек пересечения не имеют - система несовместна и решений не имеет.

Данную систему (3) можно решить методом Крамера с помощью определителей третьего порядка.

Введем понятие матрицы и определителя третьего порядка.

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА

Определение: Квадратной матрицей 3 -го порядка называется таблица чисел, которая состоит из 3-х строк и 3-х столбцов и обозначается:

А = ,

где а_i,j - называются элементами матрицы, индексы: i = 1, 2, 3 - определяет номер; строки, j = 1, 2, 3 - номер столбца. Элементы а₁₁а₂₂а₃₃ образуют главную диагональ матрицы, а элементы а₁₃а₂₂а₃₁ образуют побочную диагональ матрицы.

Каждая матрица характеризуется своим определителем.

Определение: Определителем матрицы 3-го порядка называется число, которое вычисляется методом диагоналей – как разность суммы произведений элементов главных диагоналей и суммы произведений элементов побочных диагоналей.

Определитель 3-го порядка обозначается и вычисляется по следующей схеме:

Существует другой, универсальный способ вычисления определителей 3-го порядка, который называется методом разложения и реализуется по следующей схеме:

Данная формула называется формулой разложения по элементам 1-ой строки. Эта формула позволяет вычисление определителя 3-го порядка свести к вычислению определителей 2-го порядка.

Для раскрытия сущности этой формулы введем два понятия - минора и алгебраического дополнения.

Определение: Минором М_ij элемента a_ij определителя 3-го порядка называется определитель 2-го порядка, полученный путем вычеркивания i - строки и j - столбца, на пересечении которых стоит данный элемент.

Так, для a₁₁ соответствует минор M₁₁ = , для a₁₂ - минор M₁₂= , а для а₁₃- минор M₁₃ = .

Определение: Алгебраическим дополнением А_ij элемента a_ij называется его минор М_ij, взятый со знаком +, если сумма номеров строки и столбца, в которых стоит элемент, четная и со знаком -, если эта сумма нечетная, т.е.: A_ij = (-1)^i+j M_ij.

Например: A₁₁ = (-1)¹⁺¹ M₁₁ = M₁₁; A₁₂ = (-1)¹⁺² M₁₂ = -M₁₂; A₁₃ = (-1)¹⁺³ M₁₃ = M_13.

Схема чередования знаков миноров для соответствующих элементов матрицы: .

Исходя из этих понятий, формулу разложения по элементам 1-ой строки при вычислении определителя 3-го порядка можно записать так: .

Определитель может быть разложен по любой строке или столбцу и равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Этот способ вычисления определителей называется методом разложения. Он универсален и применим для определителей любого порядка.

Перейдем к решению системы линейных уравнений с тремя неизвестными методом Крамера.

Систему: (3) путем последовательного исключения неизвестных х, у и z можно привести к равносильной (эквивалентной) системе (4), имеющей одинаковые решения с исходной системой (3): (4), где - определитель системы, , , - определители неизвестных x, y, z, которые получаются из определителя системы путем замены столбца коэффициентов при неизвестном на столбец свободных членов.

При решении системы (4) возможны 3 случая при выполнении следующих условий:

Если определитель системы , то, поделив обе части уравнений системы на , найдем неизвестные по формулам Крамера:

При первом условии система имеет единственное решение, она совместна и определена. Три плоскости пересекаются в одной точке с координатами (х₀, у₀, z₀).

1. Если определитель системы и все определители неизвестных , то имеем 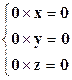и при любых значениях x, y и z имеем верное тождество.

При втором условии система имеет бесконечное множество решений, она совместна, но не определена. Плоскости совпадают друг с другом.

2. Если определитель системы , а определители неизвестных могут быть или или , то имеем: 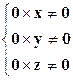, что невозможно при любых значениях х и у.

При третьем условии система решения не имеет, она не совместна. Плоскости параллельны друг другу и общих точек не имеют.

Метод решения системы линейных уравнений с помощью определителей называется методом Крамера.

Пример. Решить систему линейных уравнений методом Крамера:

1.

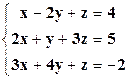
Решение:

1) Вычислим определители системы и неизвестных D, D_х, D_у и D_z.

а) методом разложения по 1-ой строке:

б) методом диагоналей:

2) Найдем решение системы по формулам Крамера:

х₀ ; у₀ = z₀ =

Проверка: Þ 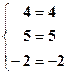(верно).

Ответ: (х₀=0, у₀= -1, z₀=2)-точка пересечения плоскостей.

1.3. Решение системы линейных уравнений с помощью матриц

Рассмотрим систему линейных уравнений с многими переменными:

, (5)

где a_ij - коэффициенты при неизвестных х_i; bi -свободные члены;

индексы: i = 1,2,3…m - определяют номер уравнения и j = 1,2,3...n - номер неизвестного.

Определение: Решением системы уравнений (5) называется совокупность n чисел (х₁₀, х₂₀,….х_n0), при подстановке которых в систему все уравнения обращаются в верные числовые тождества.

Определение: Система уравнений называется совместной, если она имеет хотя бы одно решение. Совместная система называется определенной, если она имеет единственное решение (х₁₀, х₂₀,….х_n0), и неопределенной, если таких решений несколько.

Определение: Система называется несовместной, если она не имеет решения.

Определение: Таблицы, составленные из числовых коэффициентов (a_ij) и свободных членов (bi) системы уравнений (5), называются матрицей системы (А) и расширенной матрицей (А₁), которые обозначаются в виде:

А= и А₁ = .

Определение: Матрица системы А, имеющая неравное число строк и столбцов (n≠m), называется прямоугольной. Если число строк и столбцов совпадает (n=m), то матрица называется квадратной.

Если в системе число неизвестных равно числу уравнений (n=m), то система имеет квадратную матрицу n-го порядка.

Выделим в матрице А k -произвольных строк и k -произвольных столбцов (k£m, k£n).

Определение: Определитель k- порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k- порядка матрицы А.

Рассмотрим всевозможные миноры матрицы А. Если все миноры (k+1)-порядка равны нулю, а хотя бы один из миноров k -порядка не равен нулю, то говорят, что матрица имеет ранг равный k.

Определение: Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Ранг матрицы обозначается через r(A).

Определение: Всякий отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным.

Определение: Если для двух матриц А и В их ранги совпадают r(A)= r(В), то эти матрицы называются эквивалентными и обозначаются А ~ В.

Ранг матрицы не изменится от элементарных, эквивалентных преобразований, которые включают:

1. Замену строк столбцами, а столбцов - соответствующими строками;

2. Перестановку строк или столбцов местами;

3. Вычеркивание строк или столбцов, все элементы которых равны нулю;

4. Умножение или деление строки или столбца на число, отличное от нуля;

5. Прибавление или вычитание элементов одной строки или столбца из другой, умноженной на любое число.

При определении ранга матрицы используют эквивалентные преобразования, с помощью которых исходную матрицу приводят к ступенчатой (треугольной) матрице.

В ступенчатой матрице под главной диагональю располагаются нулевые элементы, причем первый ненулевой элемент каждой её строки, начиная со второй, расположен правее первого неравного нулю элемента предыдущей строки.

Отметим, что ранг матрицы равен числу ненулевых строк ступенчатой матрицы.

Например, матрица А= ~ - ступенчатого вида и её ранг равен числу ненулевых строк матрицы r(A)=3. Действительно, все миноры 4-го порядка с нулевыми элементами 4-ой строки равны нулю, а миноры 3-го порядка отличны от нуля. Для проверки вычислим определитель минора первых 3-х строк и3-х столбцов:

М=

Любую матрицу можно привести к ступенчатой путем обнуления элементов матрицы под главной диагональю с помощью элементарных действий.

Вернемся к исследованию и решению системы линейных уравнений (5).

Важную роль в исследовании систем линейных уравнений играет Теорема Кронекера-Капели. Сформулируем эту теорему.

Теорема Кронекера-Капели: Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы А₁, т.е. r(A)=r(A₁). В случае совместности система является определенной, если ранг матрицы системы равен числу неизвестных, т.е. r(A)=r(A₁)=n и неопределенной, если этот ранг меньше числа неизвестных, т.е. r(A)= r(A₁)<n.

Пример. Исследовать систему линейных уравнений:

Решение:

Определим ранги матрицы системы А и расширенной матрицы А₁. Для этого составим расширенную матрицу А₁ и приведем её к ступенчатому виду.

При приведении матрицы выполним следующие действия:

1) вычтем из 2-ой строки 1-ю строку;

2) вычтем из 3 и 4 строк 1-ю строку, умноженную на 4;

3) умножим 4-ю строку на (-1) и поменяем местами со 2-ой строкой;

4) сложим 3 и 4 строки со 2-й строкой, умноженной соответственно на 5 и 4;

5) вычитаем из 4-ой строки 3-ю и вычеркиваем 4-ю строку с нулевыми элементами.

А₁= ~ ~ ~

~ ~ ~

В результате выполненных действий получили ступенчатую матрицу с тремя ненулевыми строками как в матрице системы (до черты), так и в расширенной матрице. Откуда видно, что ранг матрицы системы равен рангу расширенной матрицы и равен 3, но меньше числа неизвестных (n=4).

Ответ: т.к. r(A)=r(A₁)=3<n=4, то согласно теореме Кронекера-Капели система совместна, но не определена, имеет бесконечное множество решений.

В связи с тем, что ранг матриц удобно определять путем приведения их к ступенчатому виду, рассмотрим способ решения системы линейных уравнений методом Гаусса.

метод Гаусса

Сущность метода Гаусса заключается в последовательном исключении неизвестных путем приведения к ступенчатому виду расширенной матрицы А₁, которая включает до черты матрицу системы А. При этом одновременно определяются ранги матриц А, А₁ и проводится исследование системы по теореме Кронекера-Капели. На последнем этапе решают систему уравнений ступенчатого вида, делая подстановки снизу вверх найденных значений неизвестных.

Рассмотрим применение метода Гаусса и теоремы Кронекера-Капели на примере.

Пример. Решить систему методом Гаусса:

Решение:

Определим ранги матрицы системы А и расширенной матрицы А₁. Для этого составим расширенную матрицу А₁ и приведем её к ступенчатому виду. При приведении выполним следующие действия:

1) вычтем из 2-ой строки 1-ю строку;

2) вычтем из 3-ей строки 1-ю строку, умноженную на 2;

3) разделим 2-ю строку на (-2),а 3-ю строки умножим на (-1) и поменяем их местами.

А₁= ~ ~ ~

Получили ступенчатую матрицу, у которой число строк равно 3, причем у матрицы системы (до черты) также нет нулевых сток. Следовательно, ранги матрицы системы и расширенной матрицы равны 3 и равны числу неизвестных, т.е. r(A)=r(A₁)=n=3.. Согласно теореме Кронекера-Капели система совместна и определена, имеет единственное решение.

В результате преобразования матрицы А₁, обнуляя коэффициенты при неизвестных, последовательно исключили их из уравнений и получили ступенчатую (треугольную) систему уравнений:

↔ ↔

Двигаясь последовательно снизу вверх, подставляя решение (х₃=1) из третьего уравнения во второе, а решения (х₂=1, х₃=1) из второго и третьего уравнений в первое, получим решение системы уравнений: х₁=1,х₂=1, х₃=1.

Проверка: ↔ (!) Ответ: (х₁=1,х₂=1, х₃=1).

метод Жордано-Гаусса

Данную систему можно решить усовершенствованным методом Жордано-Гаусса, который заключается в том, что матрицу системы А в расширенной матрице (до черты) приводят к единичной матрице: Е= с единичными диагональными и нулевыми недиагональными элементами и получают сразу решение системы без дополнительных подстановок.

Решим рассмотренную выше систему методом Жордано-Гаусса. Для этого преобразуем полученную ступенчатую матрицу в единичную, выполнив следующие действия:

1) вычтем из 1-ой строки 2-ю строку;

2) сложим с 1-ой строкой 3-ю строку, умноженную на 3;

3) вычтем из 2-ой строки 3-ю строку, умноженную на 4.

А₁₌ ~ ~

Исходная система уравнений свелась к системе: , которая и определяет решение.

основные действия с матрицами

Пусть даны две матрицы: А= B= .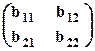

1. Матрицы равны А=В, если равны их одноименные элементы: a_ij=b_ij

2. Суммой (разностью) матриц (А ± В) называется матрица, определяемая равенством: А±В= ± = .

При суммировании (вычитании) матриц складываются (вычитаются) их одноименные элементы.

3. Произведением числа k на матрицу A называется матрица, определяемая равенством: kA=k = .

При умножении матрицы на число умножаются на это число все элементы матрицы.

4. Произведением матриц АВ называется матрица, определяемая равенством:

АВ= * = .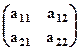

При умножении матриц элементы строк первой матрицы умножаются на элементы столбцов второй матрицы и суммируются, причем элемент матрицы-произведения, стоящий в i- й строке и j- м столбце, равен сумме произведений соответственных элементов i- й строки первой матрицы и j- м столбца второй матрицы.

При умножении матриц в общем случае переместительный закон не действует, т.е. АВ≠ВА.

5. Транспонированием матрицы А называется действие, приводящее к замене строк столбцами, а столбцов - соответствующими строками.

Матрица А^Т = называется транспонированной матрицей для матрицы А= .

Если определитель матрицы А не равен нулю (Δ≠0), то такую матрицу называют невырожденной. Для всякой невырожденной матрицы А существует обратная матрица А^-1, для которой выполняется равенство: А^-1 А= А А^-1=Е, где Е= - единичная матрица.

6. Обращением матрицы А называется такие действия, при которых получается обратная матрица А^-1

При обращении матрицы А выполняются следующие действия:

1. Вычисляется определитель матрицы Δ≠0;

2. Для каждого элемента a_ij путем вычеркивания i-строки и j-столбца определяются миноры Mij и вычисляются их алгебраические дополнения Aij==(-1)^I+j Mij

3. Cоставляется матрица из алгебраических дополнений (Aij) и транспонируется (Aij)^Т.

4. Составляется обратная матрица по формуле:

А^-1= =

матричный метод решения системы линейных уравнений с использованием обратной матрицы

Рассмотрим систему линейных уравнений c n неизвестными, имеющей вид:

(6)

Составим квадратную матрицу системы: А= .

Таблица чисел, состоящая только из одного столбца называется матрицей-столбцом или вектором-столбцом.

Введем матрицы-столбцы для неизвестных и свободных членов:

Х= .

Используя основные действия над матрицами, систему линейных уравнений (6) можно представить в матричном виде: А*Х = В (7).

Так, для системы с двумя неизвестными матричный вид будет:

А*Х=В Þ * Þ

Матричное представление системы позволяет непосредственно получить её решение с использованием обратной матрицы.

Действительно, умножим обе части матричного уравнения (7) на обратную матрицу А^-1, получим: А^-1АХ= А^-1В. Учитывая, что А^-1А=Е - единичная матрица и Е*Х=Х, окончательно получим решение системы линейных уравнений в матричном виде: Х=А^-1*В – это формула решения системы линейных уравнений матричным методом с помощью обратной матрицы.

Пример: Решить систему уравнений матричным методом:

Решение: 1)Составим матрицу системы: А= ;

2)Вычислим определитель системы D:

3) Вычислим алгебраические дополнения матрицы системы:

А₁₁=(-1)² =1-12= -11; А₁₂=(-1)³ =-2+9=7 А₁₃=(-1)⁴ =8-3=5

А₂₁=(-1)³ =2+4=6 А₂₂=(-1)⁴ =1-3=-2 А₂₃=(-1)⁵ =-4-6=-10

А₃₁=(-1)⁴ =-6-1=-7 А₃₂=(-1)⁵ =-3+2=-1 А₃₃=(-1)⁶ =1+4=5

4) Составим обратную матрицу:

А^-1= = =

5) Находим матрицу-столбец решений по формуле: Х=А^-1В

= * =

6) Выписываем решение системы: х₀=0; у₀=-1;z₀=2

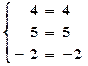Проверка: (верно).

Ответ: (х₀=0; у₀=-1;z₀=2) – координаты точки пересечения плоскостей

2. элементы Векторной алгебры

2.1. векторные и скалярные величиы

Величины бывают скалярные и векторные.

Скалярные величины задаются только их численным значением. К скалярным величинам относят такие величины как: температура, работа, длина, площадь, объем и т. д. Скаляр – это число.

Векторные величины характеризуются как численным значением (длиной), так и направлением в пространстве. К векторным величинам относят: силу, скорость, ускорение и т.д.

Дадим ряд определений.

Определение: Вектором называется направленный отрезок в пространстве, имеющий начало и конец.

Вектор обозначается = , где А – начало или точка приложения вектора, В - конец вектора. Вектор показывается отрезком со стрелкой на конце:

B

A

Вектор характеризуется длиной и направлением в пространстве.

Определение: Длина вектора называется модулем вектора и обозначается: .

Определение: Векторы и называются коллинеарными (), если они лежат на одной или параллельных прямых.

Определение: Векторы и называются равными ( = ), если выполняются три условия:

1) они коллинеарны;

2) имеют равные модули; =

3) сонаправлены.

Определение: Векторы и 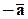называются противоположными, если выполняются три условия:

1) они коллинеарны;

2) имеют равные модули;

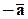
3) противоположно направлены.

Определение: Векторы называются свободными, если их можно перемещать в пространстве параллельно самим себе.

Далее рассматриваем свободные векторы.

Определение: Векторы называются компланарными, если они лежат в одной или параллельных плоскостях. Компланарные векторы всегда можно свести в одну плоскость.

Определение: Векторы называются ортогональными, если они взаимно перпендикулярны друг другу.

2.2. геометрические методы линейных операций над векторами

К линейным операциям над векторами относятся: сложение, вычитание векторов и умножение их на число (на скаляр). Линейные операции над векторами могут выполняться геометрическими методами и аналитическим способом с помощью координат векторов.

Рассмотрим геометрические методы.

СЛОЖЕНИЕ ВЕКТОРОВ

Определение: Суммой двух векторов и называется вектор , идущий из начала первого в конец второго , при условии, что второй вектор приложен к концу первого.

Метод сложения векторов, данный в определении называется методом треугольника.

Сложения векторов можно выполнять также методом параллелограмма, в котором слагаемые векторы прикладывают в одну точку. По этим векторам, как по сторонам строят параллелограмм и их суммой является вектор, идущий по диагонали из общей точки в противоположную вершину.

При сложении нескольких векторов используется метод многоугольника, который заключается в последовательном применении метода треугольника и сумма векторов представляет собой вектор, идущий из начала первого в конец последнего, когда каждый следующий вектор прикладывается к концу предыдущего. Например, сумма представляет собой вектор, идущий из начала в конец вектора _.

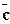
Свойства суммы векторов:

1. Переместительное свойство: ;

2. Сочетательное свойство: .

ВЫЧИТАНИЕ ВЕКТОРОВ

Определение: Разностью двух векторов и называется вектор , который в сумме с вектором дает вектор , т.е. .

Геометрически разность векторов это вектор, идущий из конца вычитаемого вектора в конец уменьшаемого вектора , если эти векторы приложены к одной точке. При чем вектор является второй диагональю в параллелограмме.

Часто вычитание векторов заменяется на сложение с использованием противоположного вектора (), при этом применяется метод треугольника.

УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (СКАЛЯР)

Определение: Произведением вектора на число k называется вектор , который

1) коллинеарен вектору , т.е. ║ ;

2) имеет длину ;

3) сонаправлен вектору , если k>0 или противоположно направлен, если k<0.

Геометрически операция умножения вектора на число приводит либо к удлинению (при k>1), либо к укорочению (при 0<k<1), либо к изменению направления на противоположное (при k<0). При этом результирующий вектор всегда коллинеарен вектору , т.е. ║ . Исходя из последнего вытекает условие коллинеарности векторов.

Условие коллинеарности векторов: два вектора коллинеарны , если они пропорциональны друг другу, т.е. выполняется условие: .

Пример: Дан вектор . Построить вектора 1,5 и -1/3 .

1,5 -1/3

Свойства операции умножения вектора на число

1. Распределительное свойство относительно суммы (разности) векторов:

;

2. Распределительное свойство относительно числовых множителей:

;

3. Сочетательное свойство относительно числовых множителей:

.

Линейные операции над вектором можно выполнять аналитическим способом с помощью координат векторов, не прибегая к геометрическим построениям.

Перейдем к координатной форме векторов.

2.3. Координатная форма векторов

Введем понятия компоненты и проекции вектора на координатную ось Ох.

Пусть координатная ось Ох задана началом координат (точкой О), положительным направлением оси Ох и единичным масштабным отрезком. Масштаб и положительное направление оси зададим в виде единичного вектора-орта , имеющего единичную длину и направленного вдоль положительного направления координатной оси.

Из начала и конца вектора опустим на ось Ох перпендикуляры. Координаты х_н, х_к - являются координатами проекций Ах и Bx начала и конца вектора.

B

A

х_Н х_К

O x

Определение: Компонентой (или составляющей) вектора на координатную ось Ох называется вектор: