Множественная регрессия представлена в виде:
+— 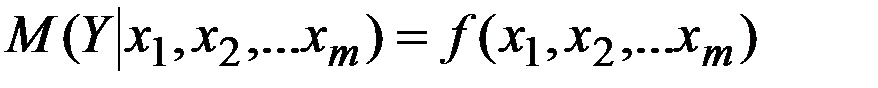
— 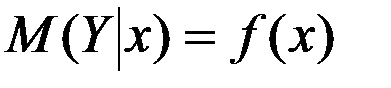
— 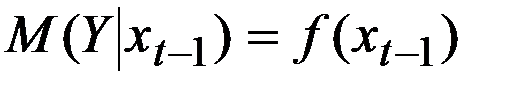
— 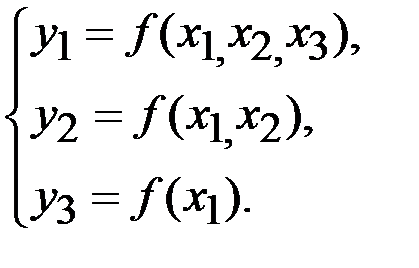
Статистическая надежность оценки коэффициентов регрессии увеличивается:
+— с увеличением числа степеней свободы;
— с уменьшением числа степеней свободы;
— не зависит от числа степеней свободы.
Добавление новой объясняющей переменной:
+— никогда не уменьшает значение коэффициента детерминации;
— иногда уменьшает значение коэффициента детерминации;
— не оказывает влияния на значение коэффициента детерминации;
Проверка статистического качества уравнения регрессии включает:
+— проверку статистической значимости коэффициентов уравнения, общего качества уравнения, выполнимости предпосылок МНК;
— проверку статистической значимости коэффициентов уравнения и выполнимости предпосылок МНК;
— вычисление доверительных интервалов зависимой переменной и проверку общего качества уравнения.
Укажите верное утверждение о скорректированном коэффициенте детерминации:
+— скорректированный коэффициент детерминации меньше обычного коэффициента детерминации для m > 1;
— скорректированный коэффициент детерминации больше обычного коэффициента детерминации для m > 1;
— скорректированный коэффициент детерминации меньше или равен обычному коэффициенту детерминации для m > 1.
С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
+— растет медленнее, чем обычный коэффициент детерминации;
— не изменяется;
— превышает значение обычного коэффициента детерминации.
Скорректированный коэффициент детерминации увеличивается при добавлении новой объясняющей переменной тогда и только тогда:
+— когда t-статистика для этой переменной по модулю больше единицы;
— когда t-статистика для этой переменной по модулю больше своего критического значения;
— когда t-статистика для этой переменной по модулю больше трех.
Если коэффициент детерминации равен нулю, то:
+— величина зависимой переменной Y линейно не зависит от независимых переменных Xi;
— величина зависимой переменной Y линейно зависит от независимых переменных Xi;
— нельзя сделать вывод о линейной зависимости Y от независимых переменных Xif.
При добавлении существенной объясняющей переменной Х в линейную модель множественной регрессии скорректированный коэффициент детерминации:
+— увеличивается;
— уменьшается;
— не изменяется.
Укажите истинное утверждение:
+— скорректированный и обычный коэффициенты детерминации совпадают только в тех случаях, когда обычный коэффициент детерминации равен единице или нулю;
— стандартные ошибки коэффициентов регрессии определяются значениями всех коэффициентов регрессии;
— при наличии гетероскедастичности оценки коэффициентов регрессии становятся смещенными.
Если коэффициент детерминации равен нулю, то критерий Фишера равен:
+— нулю;
— единице;
— больше или равен единице.
Коэффициент детерминации является мерой сравнения качества:
+— регрессионных моделей с одинаковой спецификацией и одинаковым числом наблюдений n;
— любых регрессионных моделей;
— регрессионных моделей с одинаковым числом наблюдений.
Число степеней свободы для остаточной суммы квадратов отклонений в линейной модели множественной регрессии равно:
+— n-m-1;
— n-1;
— m.
Число степеней свободы для регрессионной суммы квадратов отклонений в линейной модели множественной регрессии равно:
+— m;
— n-m-1;
— n-1.
Уравнение регрессии является качественным, если:
+— t-статистики, F-статистика больше критических значений, предпосылки МНК соблюдены;
— t-статистики, F-статистика, DW-статистика высокие;
— коэффициент детерминации больше 0,8.
Известно, что при фиксированном значении переменной x2 между переменными y и х1 существует положительная связь. Какое значение может принять частный коэффициент корреляции Rух1/x2?
+— 0,4;
— 0;
— -0,8;
— 1,3.
Множественный коэффициент корреляции Rух1x2 = 0,8. Определите, какой процент дисперсии зависимой переменной у объясняется влиянием х1 и x2:
— 80%;
— 28%;
— 32%;
+— 64%.
По результатам 20 наблюдений найден множественный коэффициент корреляции Rух1x2 = 0,8. Проверьте значимость Rух1x2 при уровне значимости 0,05 и определите разность между наблюдаемым и критическим значениями критерия Фишера:
+— 11.5;
— 2.8;
— 13.6;
— 9.4.
Какое значение может принимать коэффициент детерминации:
+— 0.4;
— - 0,5;
— - 0,2;
— 1,2.
Какое значение не может принять множественный коэффициент корреляции:
+— 1,2;
— -1;
— -0.5;
— 0.
Известно, что х2 усиливает связь между у и х1. По результатам наблюдений получен частный коэффициент корреляции Rух1/x2 = -0,45. Какое значение может принять парный коэффициент корреляции rух1?
+— -0.3;
— 0.4;
— 0.2;
— 1.2.
По результатам наблюдений получен парный коэффициент корреляции rух1 = 0.6. Известно, что х2 занижает связь между у и х1. Какое значение может принять частный коэффициент корреляции?
— 0.8;
+— 0.5;
— -0.5;
— -0.6.
Какие требования в линейной модели множественной регрессии предъявляются к математическому ожиданию и дисперсии случайных отклонений:
+— 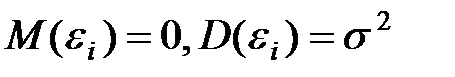
— 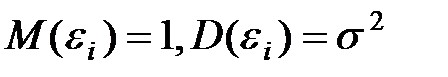
— 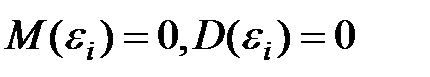
— 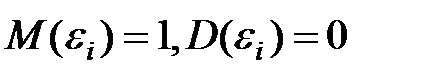
Что минимизируется согласно методу наименьших квадратов?
+— 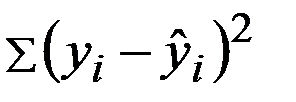
— 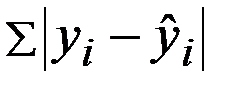
— 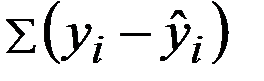
— 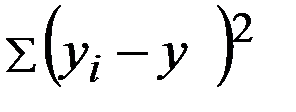
Если эффективность производства растет по мере его укрупнения и оно описывается производственной функцией Кобба-Дугласа, то параметры модели удовлетворяют соотношению:
+— 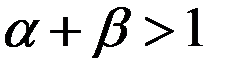
— 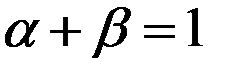
— 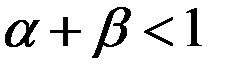
— 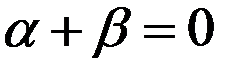
Получена производственная функция Y = 2.7*K 0.8*L 0.2, если объем капитала К увеличить на 1%, то объем производства в среднем изменится (в %) на:
+— 0.8;
— 2.7;
— 0.2;
— -0.8.
Получены две производственные функции Кобба-Дугласа, имеющие равные значения параметров «альфа» и «бета», но различающиеся по параметру А. В каком случае первое производство более эффективно, чем второе?
+— А1 > А2;
— A1 < A2;
— A1 = A2.
По 26 наблюдениям получена модель производственной функции:
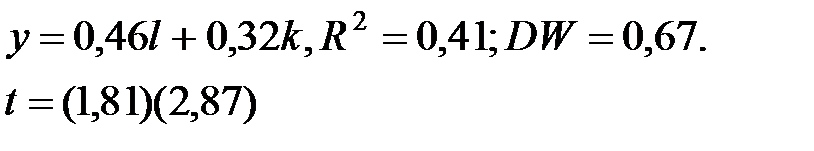 y, l, k - темпы прироста объема выпуска, затрат труда и капитал. Какой вывод является верным:
y, l, k - темпы прироста объема выпуска, затрат труда и капитал. Какой вывод является верным:
+— надо исключить фактор l, так как он оказался статистически незначим;
— надо исключить фактор k, так как он оказался статистически незначим;
— модель имеет удовлетворительные статистики, поэтому нет смысла ее совершенствовать.
В чем состоит условие гомоскедастичности в регрессионной модели:
— 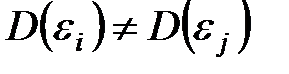
— 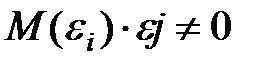
+— 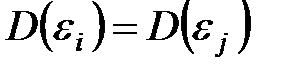
— 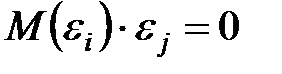
На практике гетероскедастичность имеет место, если есть основания считать, что:
+— вероятностные распределения случайных отклонений при различных наблюдениях будут различны;
— вероятностные распределения случайных отклонений при различных наблюдениях будут одинаковы;
— дисперсии случайных отклонений постоянны.
При гетероскедастичности случайных отклонений оценки коэффициентов регрессии становятся:
+— неэффективными;
— смещенными;
— нелинейными.
При гетероскедастичности, вероятнее всего, что t-статистики коэффициентов регрессии и F-статистика будут:
+— завышенные;
— заниженные;
— точные.
В координатной плоскости при гомоскедастичности случайных отклонений:
+— квадраты случайных отклонений находятся внутри полуплоскости, параллельной оси абсцисс;
— квадраты случайных отклонений находятся в первой четверти системы координат;
— наблюдаются систематические изменения в соотношениях между квадратами случайных отклонений и переменной Х.
Какое из утверждений верно:
+— не существует общего теста для анализа гетероскедастичности;
— тест ранговой корреляции Спирмена основан на использовании статистики Фишера;
— тест Глейзера является частным случаем теста Голдфелда-Квандта.
В условиях автокорреляции t-статистики коэффициентов регрессии будут:
+— завышены;
— занижены;
— точные.
Если график наблюдений переменной Y и график регрессионных значений переменной Y пересекаются редко, то можно предположить наличие:
+— положительной автокорреляции остатков;
— отрицательной автокорреляции остатков;
— отсутствие автокорреляции остатков.
Преобразование соответствует: 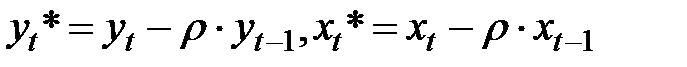
+— авторегрессионной схеме 1 порядка;
— методу взвешенных наименьших квадратов;
— косвенному методу наименьших квадратов.
Для обнаружения автокорреляции применяют:
+— критерий DW;
— тест Голдфелда-Квандта;
— тест Спирмена;
— тест Глейзера.
Статистика DW изменяется в пределах:
+— от нуля до четырех;
— от нуля до двух;
— меньше или равна двум.
Коэффициент автокорреляции «ро» в авторегрессионной схеме 1 порядка на основе статистики DW определяется:
+— 1-DW/2;
— DW/2;
— 1+DW/2.
Метод первых разностей применяется для определения коэффициента автокорреляции «ро» тогда, когда:
+— 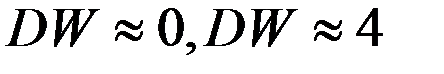
— 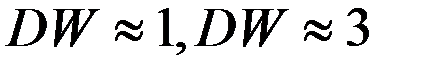
— 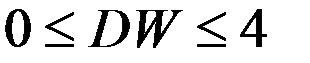
Укажите ложное утверждение:
+— при наличии автокорреляции значение коэффициента детерминации всегда будет существенно ниже единицы;
— статистика DW лежит в пределах от 0 до 4;
— статистика DW не используется в авторегрессионных моделях.
Мультиколлинеарность – это:
+— линейная взаимосвязь двух или нескольких объясняющих переменных;
— взаимосвязь между случайными отклонениями;
— постоянство дисперсии случайных отклонений.
Признаком мультиколлинеарности является:
+— высокие коэффициент детерминации и частные коэффициенты корреляции;
— высокий DW;
— высокое значение F-статистики.
Для оценки коррелированности между двумя объясняющими переменными рассчитывают:
+— коэффициент парной линейной корреляции;
— частные коэффициенты корреляции;
— коэффициент детерминации.
Укажите ложное утверждение:
+— мультиколлинеарность не ухудшает качество модели;
— мультиколлинеарность не приводит к получению смещенных оценок коэффициентов, но ведет к получению смещенных оценок для дисперсии коэффициентов;
— при наличии мультиколлинеарности оценки коэффициентов остаются несмещенными, но их t-статистики будут занижены.
Какое из утверждений верно (применительно к гетероскедастичности):
— оценки вследствие гетероскедастичности перестают быть состоятельными;
— оценки и дисперсии оценок остаются несмещенными;
+— выводы по статистикам являются ненадежными (применительно к гетероскедастичности);
— гетероскедастичность проявляется через низкое значение статистики DW.
Что такое автокорреляция остатков?
+— взаимная зависимость остатков регрессии;
— равенство остатков регрессии;
— непостоянство дисперсии остатков;
— все перечисленное.
Критерий Дарбина-Уотсона применяется для:
+— проверки модели на автокорреляцию остатков;
— определения экономической значимости модели в целом;
— определения статистической значимости модели в целом;
— сравнения двух альтернативных вариантов модели;
— отбора факторов в модель.
Для модели, связывающей количество вакансий Wt и уровень безработицы Ut:
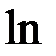 Wt = 2,3-0,78 lnUt, статистика Дарбина-Уотсона составила 0,7. О чем говорит ее значения?
Wt = 2,3-0,78 lnUt, статистика Дарбина-Уотсона составила 0,7. О чем говорит ее значения?
+— свидетельствует о наличии положительной автокорреляции первого порядка ошибок регрессии;
— свидетельствует о тесной связи между количеством вакансий и уровнем безработицы;
— свидетельствует о значимости коэффициентов регрессии;
— подтверждает наличие гетероскедастичности.
В чем суть гетероскедастичности?
+— дисперсии случайных отклонений изменяются;
— дисперсии случайных отклонений постоянны;
— случайные отклонения взаимно коррелированы;
— случайные отклонения равны для всех наблюдений.
Какое из утверждений о гетероскедастичности не верно:
— проблема гетероскедастичности обычно характерна для перекрестных данных;
— выводы по t–статистикам и F-статистике при гетероскедастичности являются ненадежными;
— не существует общего теста для анализа гетероскедастичности;
+— гетероскедастичность проявляется через низкое значение статистики Дарбина – Уотсона.
Когда дисперсии отклонений неизвестны, то для устранения гетероскедастичности применяют:
— коэффициент пропорциональности 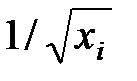 , или
, или 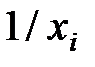
— коэффициент пропорциональности 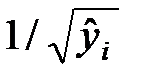
+— коэффициент пропорциональности 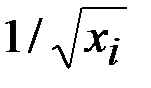 , или
, или 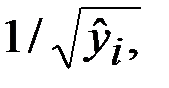 или
или 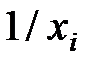
Тест Голдфелда – Кванта основан на использовании:
— t – статистики распределения Стьюдента;
+— F – статистики распределения Фишера;
— статистики Дарбина – Уотсона;
— коэффициента ранговой корреляции Спирмена.
Для регрессии: 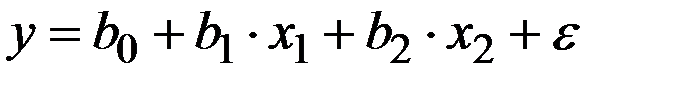 за период 1971-1998 гг. получены следующие результаты
за период 1971-1998 гг. получены следующие результаты 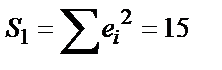 (для данных 1971-1980 гг.),
(для данных 1971-1980 гг.), 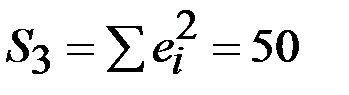 (для данных 1989-1998 гг.). Сделайте вывод о постоянстве дисперсии отклонений:
(для данных 1989-1998 гг.). Сделайте вывод о постоянстве дисперсии отклонений:
+— дисперсия отклонений непостоянна;
— дисперсия отклонений постоянна;
— дисперсия отклонений составляет 35;
— дисперсия отклонений не влияет на качество регрессии.
Укажите неверное применительно к автокорреляции выражение:
— оценки коэффициентов перестают быть эффективными;
— выводы по t- и F – статистикам могут быть неверными;
— дисперсия регрессии является смещенной оценкой истинного значения;
+— дисперсии оценок коэффициентов остаются несмещенными.
Чем скорректированный R2 отличается от обычного?
+— скорректированный R2 содержит поправку на число степеней свободы для получения несмещенных оценок дисперсии;
— скорректированный R2 всегда меньше обычного R2;
— скоректированный R2 больше, чем обычный R2;
— скорректированный R2 вычисляется намного проще, чем обычный R2.
Когда целесообразно добавление новой объясняющей переменной в модель?
— при росте R2;
+— при росте скорректированного R2;
— в любом случае;
— если модель не соответствует экономической теории.
По результатам бюджетного обследования пяти семей записано следующее уравнение регрессии накоплений (регрессоры – доход и имущество, тыс. руб.) y = 0,279 + 0,123x1-0,029x2
Спрогнозируйте накопление семьи, имеющей доход 40 тыс. руб. и имущество стоимостью 25 тыс. руб:
+— 4,47;
— 3,78;
— 5,06;
— 5,47.
По результатам бюджетного обследования пяти семей записано следующее уравнение регрессии накоплений (регрессоры – доход и имущество, тыс. руб.) y = 0,279 + 0,123x1-0,029x2
Оцените, как возрастут накопления семьи, если ее доход вырос на 10 тыс. руб.,а стоимость имущества не изменилась?
— 10,123;
+— 1,23;
— 0,123;
— 10,0.
По результатам бюджетного обследования пяти семей записано следующее уравнение регрессии накоплений (регрессоры – доход и имущество, тыс. руб.) y = 0,279 + 0,123x1-0,029x2
Оцените, как возрастут накопления семьи, если ее доход вырос на 5 тыс. руб., а стоимость имущества увеличилась на 15 тыс. руб:
— 0,20;
— 0,35;
— 0,15;
+— 0,18.
По 40 точкам оценена следующая модель производственной функции:
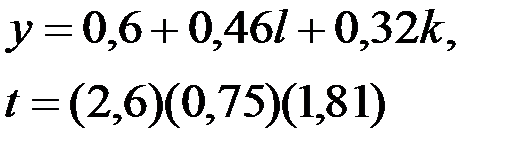
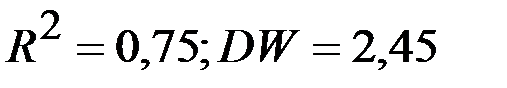
y, l, k - темпы прироста объема выпуска, затрат труда и затрат капитала. Укажите неверный вывод:
— имеет место автокорреляция остатков первого порядка, поэтому надо изменить форму зависимости;
+— надо исключить фактор l, так как он оказался статистически незначим;
— модель имеет удовлетворительные статистики, поэтому нет смысла ее совершенствовать.
Дополнительные вопросы
Замена 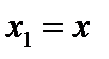 ,
, 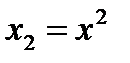 подходит для уравнения:
подходит для уравнения:
- 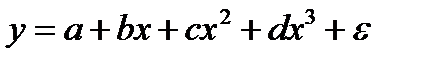 ;
;
- 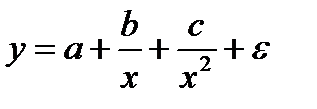 ;
;
- 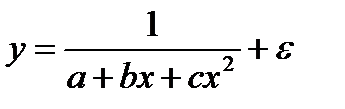 ;
;
+ 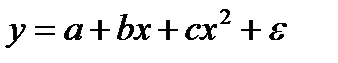 .
.
Величина остаточной дисперсии при включении существенного фактора в модель:
- не изменится;
- будет увеличиваться;
- будет равно нулю;
-+ будет уменьшаться.
Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать.
Для исследования данной зависимости можно использовать спецификацию уравнения регрессии:
- 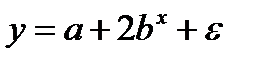 ;
;
- 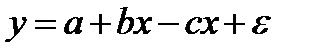 ;
;
- 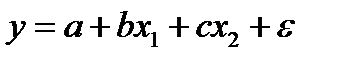 ;
;
+ 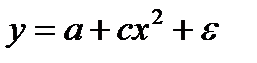 .
.
Фиктивные переменные включаются в уравнения регрессии:
- случайной;
- парной;
- косвенной;
+- множественной
Обобщенный метод наименьших квадратов не используется для моделей с остатками:
- автокоррелированными и гетероскедастичными;
+- гомоскедастичными;
- автокоррелированными.
Из пары коллинеарных факторов в эконометрическую модель включается тот фактор:
- который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами;
- который при отсутствии связи с результатом имеет максимальную связь с другими факторами;
- который при отсутствии связи с результатом имеет наименьшую связь с другими факторами;
+- который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами.
Линеаризация подразумевает процедуру:
- приведения уравнения множественной регрессии к парной;
+ приведения нелинейного уравнения к линейному виду;
- приведения линейного уравнения к нелинейному виду;
- приведения нелинейного уравнения относительно параметров к уравнению, линейному относительно результата.
После применения обобщенного метода наименьших квадратов удается избежать остатков:
+- гетероскедастичности;
- нормального распределения;
- равенства нулю суммы;
- случайного характера.
Результатом линеаризации полиномиальных уравнений является:
- нелинейные уравнения парной регрессии;
- линейные уравнения парной регрессии;
- нелинейные уравнения множественной регрессии;
+- линейные уравнения множественной регрессии.
Множественная регрессия не является результатом преобразования уравнения:
+- 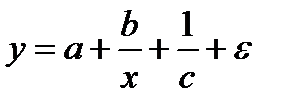 ;
;
- 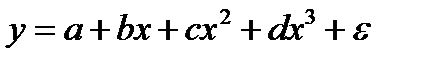 ;
;
- 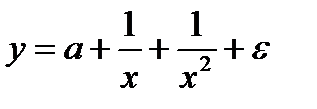 ;
;
- 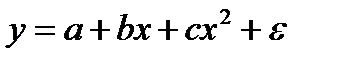 .
.
Обобщенный метод наименьших квадратов отличается от обычного МНК тем, что при применении ОМНК:
+- преобразуются исходные уровни переменных;
- остатки не изменяются;
- остатки приравниваются к нулю;
- уменьшается количество наблюдений
Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений:
- общей дисперсии до и после включения фактора в модель;
- остаточной дисперсии до и после включения случайных факторов в модель;
- дисперсии до и после включения результата в модель;
+- остаточной дисперсии до и после включения фактора модель.
В стандартизованном уравнении множественной регрессии переменными являются:
- исходные переменные;
- стандартизованные параметры;
- средние значения исходных переменных;
+- стандартизованные переменные.
Одним из методов присвоения числовых значений фиктивным переменным является:
+– ранжирование;
- выравнивание числовых значений по возрастанию;
- выравнивание числовых значений по убыванию;
- нахождение среднего значения.
Метод оценки параметров моделей с гетероскедастичными остатками называется методом наименьших квадратов:
- обычным;
- косвенным;
+- обобщенным;
- минимальным.
Дано уравнение регрессии 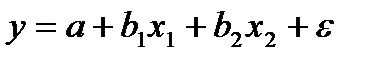 .
.
Определите спецификацию модели:
- полиномиальное уравнение парной регрессии;
- линейное уравнение простой регрессии;
- полиномиальное уравнение множественной регрессии;
+- линейное уравнение множественной регрессии.
В стандартизованном уравнении свободный член:
- равен 1;
- равен коэффициенту множественной детерминации;
- равен коэффициенту множественной корреляции;
+- отсутствует.
В матрице парных коэффициентов корреляции отображены значения парных коэффициентов линейной корреляции между:
- переменными;
- параметрами;
+- параметрами и переменными;
- переменными и случайными факторами.
В качестве фиктивных переменных в модель множественной регрессии включаются факторы:
- имеющие вероятностные значения;
- имеющие количественные значения;
- не имеющие качественных значений;
+- не имеющие количественных значений.
Факторы эконометрической модели являются коллинеарными, если коэффициент:
+- корреляции между ними по модулю больше 0,7;
- детерминации между ними по модулю больше 0,7;
- детерминации между ними по модулю меньше 0,7;
Обобщенный метод наименьших квадратов отличается от обычного МНК тем, что при применении ОМНК:
+- преобразуются исходные уровни переменных;
- остатки не изменяются;
- остатки приравниваются к нулю;
- уменьшается количество наблюдений.
Объем выборки определяется:
- числовыми значением переменных, отбираемых в выборку;
+- объемом генеральной совокупности;
- числом параметров при независимых переменных;
- числом результативных переменных.
Множественная регрессия не является результатом преобразования уравнения:
+- 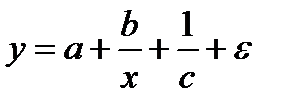 ;
;
- 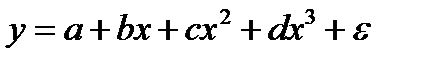 ;
;
- 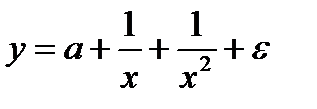 ;
;
- 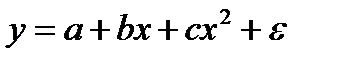 .
.
Исходные значения фиктивных переменных предполагают значения:
+- качественные;
- количественно измеримые;
- одинаковые;
- значения.
Обобщенный метод наименьших квадратов подразумевает:
+- преобразование переменных;
- переход от множественной регрессии к парной;
- линеаризацию уравнения регрессии;
- двухэтапное применение метода наименьших квадратов.
Линейное уравнение множественной регрессии имеет вид: 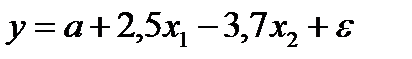 . Определите какой из факторов
. Определите какой из факторов 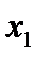 или
или 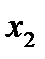 оказывает более сильное влияние на
оказывает более сильное влияние на 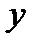 :
:
+- 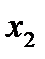 , так как 3,7 > 2,5;
, так как 3,7 > 2,5;
- оказывают одинаковое влияние;
- 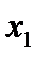 , так как 2,5 > -3,7;
, так как 2,5 > -3,7;
- по этому уравнению нельзя ответить на поставленный вопрос, так как коэффициенты регрессии несравнимы между собой.
Включение фактора в модель целесообразно, если коэффициент регрессии при этом факторе является:
- нулевым;
- незначимым;
+- существенным;
- несущественным.
Что преобразуется при применении обобщенного метода наименьших квадратов?
- стандартизованные коэффициенты регрессии;
- дисперсия результативного признака;
+- исходные уровни переменных;
- дисперсия факторного признака.
Проводится исследование зависимости выработки работника предприятия от ряда факторов.
Примером фиктивной переменной в данной модели будет являться работника:
- возраст;
- стаж;
- заработная плата.
Переход от точечного оценивания к интервальному возможен, если оценки являются:
- эффективными и несостоятельными;
- неэффективными и состоятельными;
+- эффективными и несмещенными;
- состоятельными и смещенными.
Матрица парных коэффициентов корреляции строится для выявления коллинеарных и мультиколлинеарных:
+- параметров;
- случайных факторов;
- существенных факторов;
- результатов.
На основании преобразования переменных при помощи обобщенного метода наименьших квадратов получаем новое уравнение регрессии, которое представляет собой:
- взвешенную регрессию, в которой переменные взяты с весами 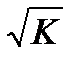 ;
;
- нелинейную регрессию, в которой переменные взяты с весами 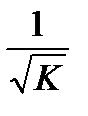 ;
;
- нелинейную регрессию, в которой переменные взяты с весами 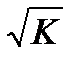 ;
;
+- взвешенную регрессию, в которой переменные взяты с весами 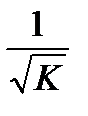 .
.
Если расчетное значение критерия Фишера меньше табличного значения, то гипотеза о статистической незначимости уравнения:
- отвергается;
- незначима;
+- принимается;
- несущественна.
Если факторы входят в модель как произведение, то модель называется:
- суммарной;
- производной;
- аддитивной;
+- мультипликативной.
Уравнение регрессии, которое связывает результирующий признак с одним из факторов при зафиксированных на среднем уровне значении других переменных, называется:
- множественным;
- существенным;
+- частным;
- несущественным.
Относительно количества факторов, включенных в уравнение регрессии, различают:
- линейную и нелинейную регрессии;
- непосредственную и косвенную регрессии;
+- простую и множественную регрессию;
- множественную и многофакторную регрессию.
Требованием к уравнениям регрессии, параметры которых можно найти при помощи МНК является:
- равенство нулю значений факторного признака4
-нелинейность параметров;
- равенство нулю средних значений результативной переменной;
- линейность параметров.
Метод наименьших квадратов не применим для:
- линейных уравнений парной регрессии;
- полиномиальных уравнений множественной регрессии;
+- уравнений, нелинейных по оцениваемым параметрам;
- линейных уравнений множественной регрессии.
При включении фиктивных переменных в модель им присваиваются:
- нулевые значения;
+- числовые метки;
- одинаковые значения;
- качественные метки.
Если между экономическими показателями существует нелинейная связь, то:
- нецелесообразно использовать спецификацию нелинейного уравнения регрессии;
- целесообразно использовать спецификацию нелинейного уравнения регрессии;
- целесообразно использовать спецификацию линейного уравнение парной регрессии;
+- необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии.
Результатом линеаризации полиномиальных уравнений является:
- нелинейные уравнения парной регрессии;
- линейные уравнения парной регрессии;
- нелинейные уравнения множественной регрессии;
+- линейные уравнения множественной регрессии.
В стандартизованном уравнении множественной регрессии 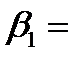 0,3;
0,3; 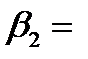 -2,1. Определите, какой из факторов
-2,1. Определите, какой из факторов 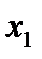 или
или 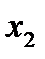 оказывает более сильное влияние на
оказывает более сильное влияние на 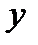 :
:
+- 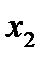 , так как 2,1 > 0,3;
, так как 2,1 > 0,3;
- по этому уравнению нельзя ответить на поставленный вопрос, так как неизвестны значения «чистых» коэффициентов регрессии;
- 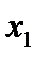 , так как 0,3 > -2,1;
, так как 0,3 > -2,1;
- по этому уравнению нельзя ответить на поставленный вопрос, так как стандартизированные коэффициенты несравнимы между собой.
Факторные переменные уравнения множественной регрессии, преобразованные из качественных в количественные называются:
- аномальными;
- множественными;
- парными;
+- фиктивными.
Оценки параметров линейного уравнения множественной регрессии можно найти при помощи метода:
- средних квадратов;
- наибольших квадратов;
- нормальных квадратов;
+- наименьших квадратов.
Основным требованием к факторам, включаемым в модель множественной регрессии, является:
- отсутствие взаимосвязи между результатом и фактором;
- отсутствие взаимосвязи между факторами;
+- отсутствие линейной взаимосвязи между факторами;
- наличие тесной взаимосвязи между факторами.
Фиктивные переменные включаются в уравнение множественной регрессии для учета действия на результат признаков:
+- качественного характера;
- количественного характера;
- несущественного характера;
- случайного характера.
Из пары коллинеарных факторов в эконометрическую модель включается тот фактор:
- который при достаточно тесной связи с результатом имеет наибольшую связь с другими факторами;
- который при отсутствии связи с результатом имеет максимальную связь с другими факторами;
- который при отсутствии связи с результатом имеет наименьшую связь с другими факторами;
+- который при достаточно тесной связи с результатом имеет меньшую связь с другими факторами.
Гетероскедастичность подразумевает:
- постоянство дисперсии остатков независимо от значения фактора;
- зависимость математического ожидания остатков от значения фактора;
+- зависимость дисперсии остатков от значения фактора;
- независимость математического ожидания остатков от значения фактора.
Величина остаточной дисперсии при включении существенного фактора в модель:
- не изменится;
- будет увеличиваться;
- будет равно нулю;
-+ будет уменьшаться.
Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение:
+- регрессии;
- детерминации;
- корреляции;
- аппроксимации.
Исследуется зависимость, которая характеризуется линейным уравнением множественной регрессии. Для уравнения рассчитано значение тесноты связи результативной переменной с набором факторов.
В качестве этого показателя был использован множественный коэффициент:
- корреляции;
- эластичности;
- регрессии;
+- детерминации.
Строится модель зависимости спроса от ряда факторов. Фиктивной переменной в данном уравнении множественной регрессии не является потребителя.
+- доход;
- семейное положение;
- пол.
Для существенного параметра расчетное значение критерия Стьюдента:
+- больше табличного значения критерия;
- равно нулю;
- не больше табличного значения критерия Стьюдента;
- меньше табличного значения критерия.
Систему МНК, построенную для оценки параметров линейного уравнения множественной регрессии можно решить:
- методом скользящего среднего;
+- методом определителей;
- методом первых разностей;
- симплекс-методом.
Показатель, характеризующий на сколько сигм изменится в среднем результат при изменении соответствующего фактора на одну сигму, при неизменном уровне других факторов, называется коэффициентом регрессии:
+- стандартизованным;
- нормализованным;
- выровненным;
- центрированным.
Мультиколлинеарность факторов эконометрической модели подразумевает:
- наличие нелинейной зависимости между двумя факторами;
- наличие линейной зависимости между более чем двумя факторами;
- отсутствие зависимости между факторами;
+- наличие линейной зависимости между двумя факторами.
Обобщенный метод наименьших квадратов не используется для моделей с остатками:
- автокоррелированными и гетероскедастичными;
+- гомоскедастичными;
- гетероскедастичными;
- автокоррелированными.
Методом присвоения числовых значений фиктивным переменным не является:
- ранжирование;
- присвоение цифровых меток;
- нахождения среднего значения;
+- присвоение количественных значений.
Обобщенный метод наименьших квадратов рекомендуется применять в случае:
- нормально распределенных остатков;
- гомоскедастичных остатков;
+- автокорреляции остатков;
- автокорреляции результативного признака.
Отбор факторов в модель множественной регрессии при помощи метода включения основан на сравнении значений:
- общей дисперсии до и после включения фактора в модель;
- остаточной дисперсии до и после включения случайных факторов в модель;
- дисперсии до и после включения результата в модель;
+- остаточной дисперсии до и после включения фактора модель.
Обобщенный метод наименьших квадратов используется для корректировки:
- параметров нелинейного уравнения регрессии;
- точности определения коэффициента множественной корреляции;
- автокорреляции между независимыми переменными;
+- гетероскедастичности остатков в уравнении регрессии.
После применения обобщенного метода наименьших квадратов удается избежать остатков:
+- гетероскедастичности;
- нормального распределения;
- равенства нулю суммы;
- случайного характера.
Фиктивные переменные включаются в уравнения регрессии:
- случайной;
- парной;
- косвенной;
+- множественной.
Взаимодействие факторов эконометрической модели означает, что:
- влияние факторов на результирующий признак зависит от значений другого неколлинеарного им фактора;
- влияние факторов на результирующий признак усиливается, начиная с определенного уровня значений факторов;
- факторы дублируют влияние друг друга на результат;
+- влияние одного из факторов на результирующий признак не зависит от значений другого фактора.
Одним из признаков мультиколлинеарности, использующий понятие Д-определителя матрицы межфакторной корреляции является выражение:
Д =< 1;
д = > 0;
Д примерно = 1;
д примерно = 0.
О присутствии мультиколлинеарности свидетельствуют величины недиагональных элементов матрицы межфакторной корреляции:
- близкие к нулю равные между собой
- по абсолютной величине превышающие значения 0.75-0.8 не превышающие по абсолютной величине 0.5
При вычислении множественного коэффициента линейной корреляции требуется:
- определить частные коэффициенты корреляции первого и второго порядков
- определить индекс корреляции по обратному уравнению связи рассматривать один из признаков в качестве результата, а другие- в качестве факторов
- рассматривать один из признаков в качестве фактора, а другие в качестве результатов
Нелинейным уравнением множественной регрессии является:
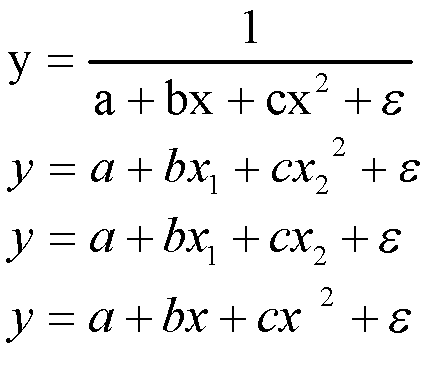
Коэффициент множественной корреляции R и любой из коэффициентов парной корреляции г находятся в следующих отношениях:
R < г;
R = г;
г > > R;
R > г.
Для вычисления коэффициента множественной корреляции требуется выявить наличие мультиколлинеарности определить ранг корреляционной матрицы из совокупности признаков выделить признак-результат и признаки-факторы, вычислить все парные коэффициенты корреляции вычислить корреляционное отношение
Оценки параметров регрессии ненадежны, имеют большие стандартные ошибки и меняются с изменением объема наблюдений, не только по величине, но и по знаку.
Это характерно для линейной модели множественной регрессии:
- при гетероскедастичности;
- при автокорреляция остатков этой модели;
- при неслучайном характере результатирующей переменной;
- при наличии в ней мультиколлинеарных факторов.
Проявление гетероскедастичности в остатках удаляется при помощи метода обобщенного метода наименьших квадратов путем (2 варианта ответа):
- расчета критерия Дарбина-Уотсона гомоскедастичных остатков;
- преобразования переменных;
- введения в модель фиктивных переменных;
- введения в выражение для дисперсии остатков коэффициента пропорциональности.
Тест Голдфелда-Квандта, используемый для обнаружения гетероскедастичности остатков основан на:
С помощью теста Гольдфельда - Квандта проверяется:
- наличие мультиколлинеарности в модели;
- наличие гетероскедостичности в остатках модели;
- наличие автокорреляции в остатках модели;
- наличие зависимости между исследуемыми переменными.
Тест Спирмена, используемый для обнаружения гетероскедастичности остатков, основан на:
- минимизации остатков;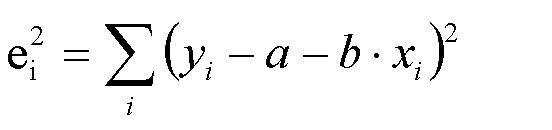
- сравнении рангов значений независимой переменной x. и остатков модели;
- предположении пропорциональности между дисперсией остатков и независимой переменной с коэффициентом;
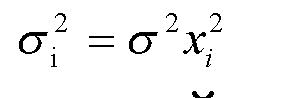
- сравнении рангов значений зависимой переменной y; и остатков модели e-
Уравнение регрессии, построенное по 15 наблюдениям, имеет вид:
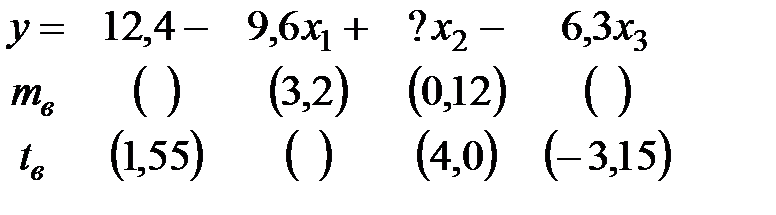
Пропущенные значения, а также доверительный интервал для
 с вероятностью 0,99 равны:
с вероятностью 0,99 равны:
+— 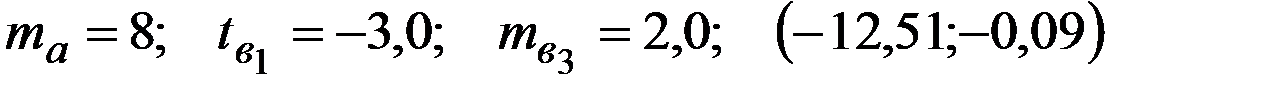
— 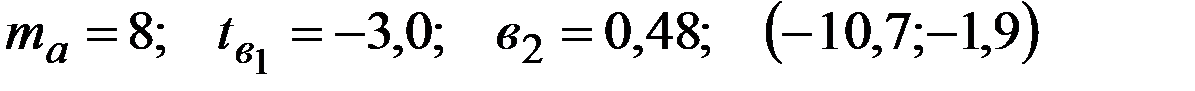
— 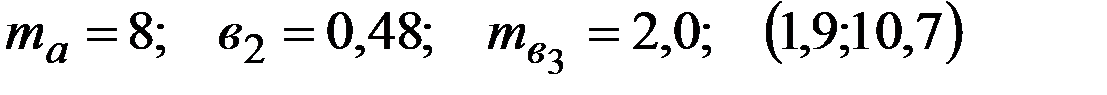
— 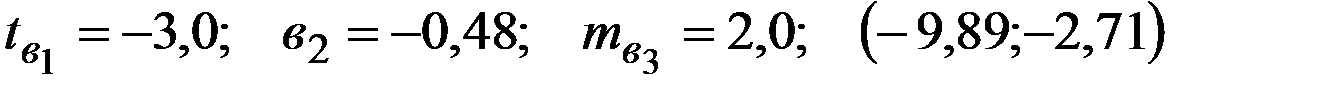
Уравнение регрессии, построенное по 20 наблюдениям, имеет вид:
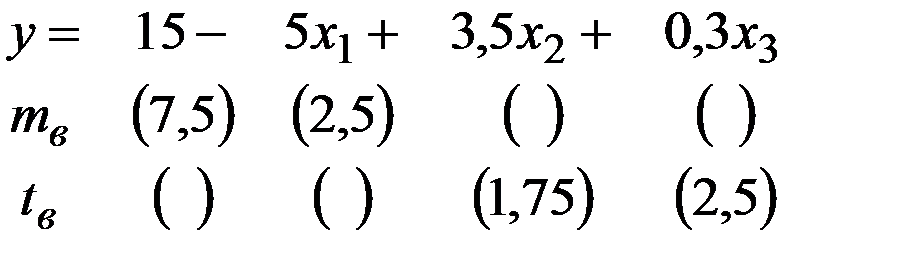
Пропущенные значения, а также доверительный интервал для 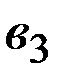 с вероятностью 0,9 равны:
с вероятностью 0,9 равны:
+— 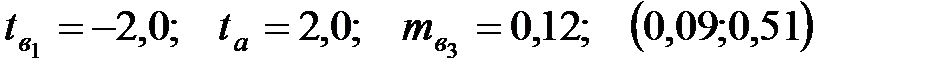
— 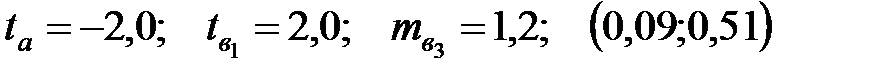
— 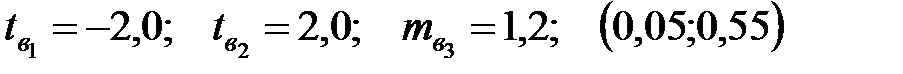
— 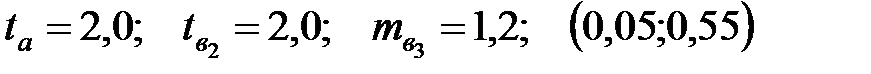
Уравнение регрессии, построенное по 16 наблюдениям, имеет вид:
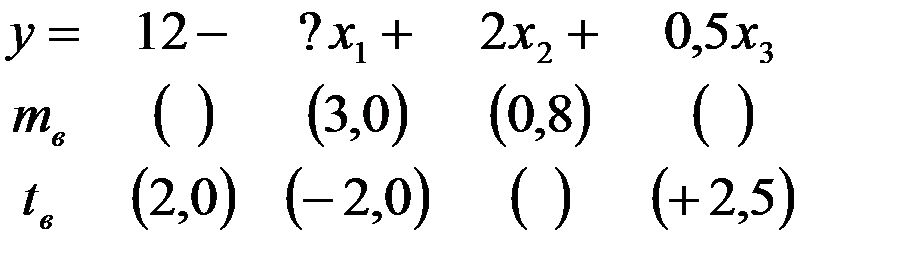
Пропущенные значения, а также доверительный интервал для 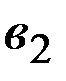 с вероятностью 0,99 равны:
с вероятностью 0,99 равны:
+— 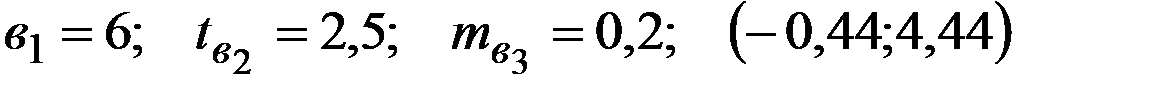
— 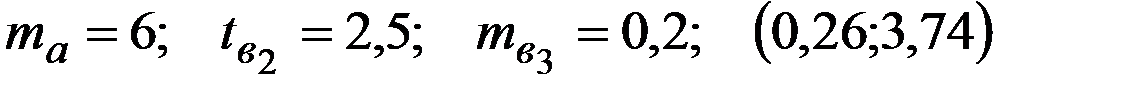
— 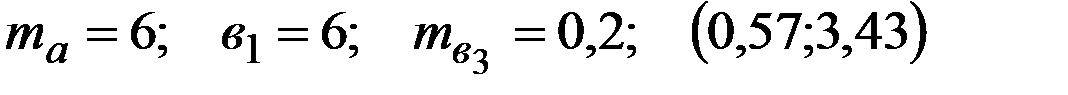
— 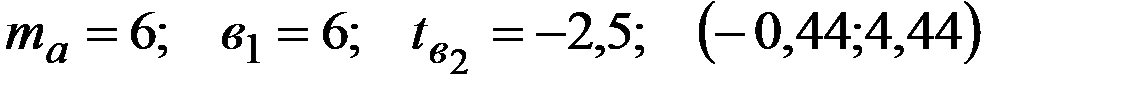
Уравнение регрессии в стандартизированном виде имеет вид:
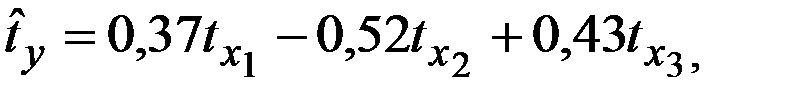
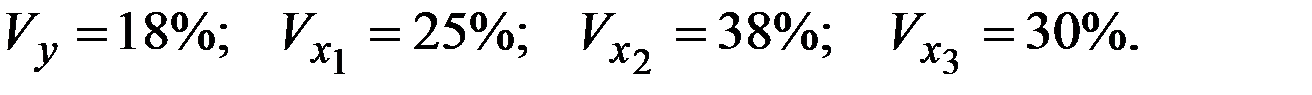
Частные коэффициенты эластичности равны:
| + |
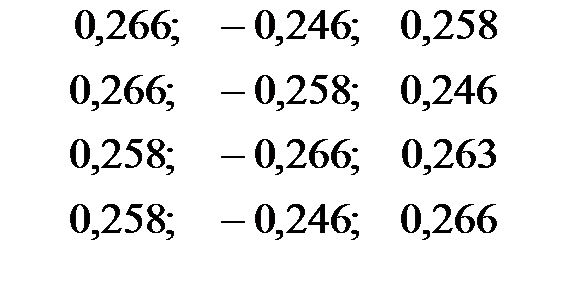
Уравнение регрессии в стандартизированном виде имеет вид:
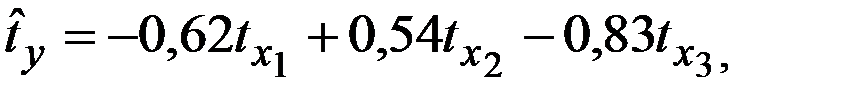
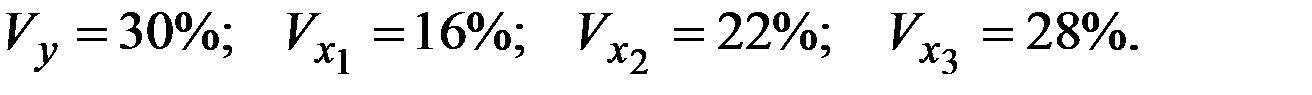
| + |
Частные коэффициенты эластичности равны:

Стандартизованное уравнение регрессии имеет вид:
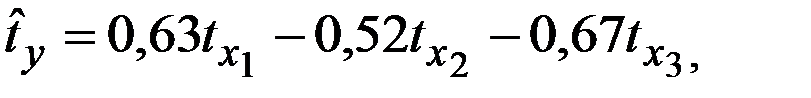
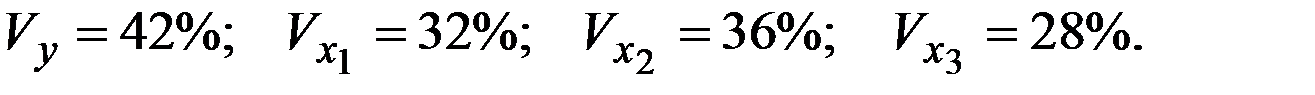
Частные коэффициенты эластичности равны:
| + |
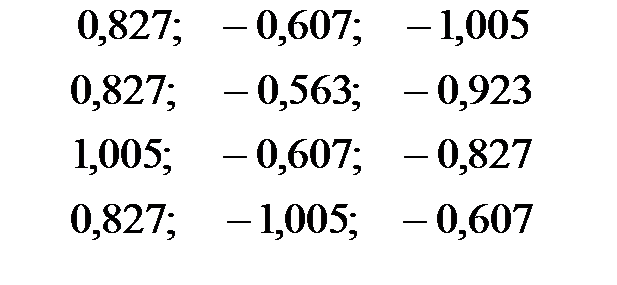
Стандартизованное уравнение регрессии имеет вид:
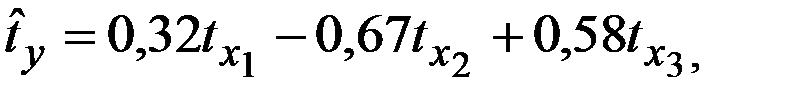
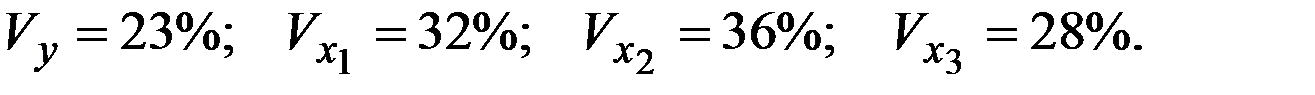
| + |
Частные коэффициенты эластичности равны:
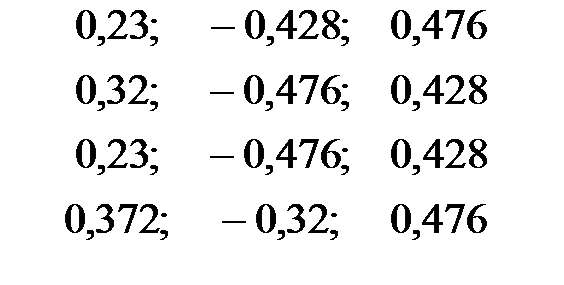
Стандартизованное уравнение регрессии имеет вид:
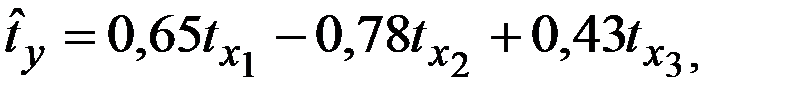
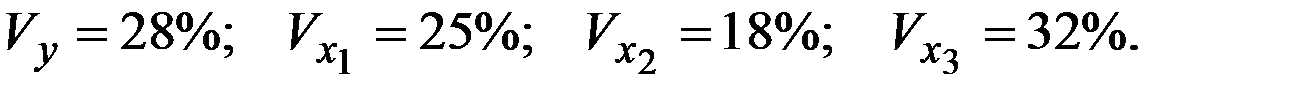
| + |
Частные коэффициенты эластичности равны:
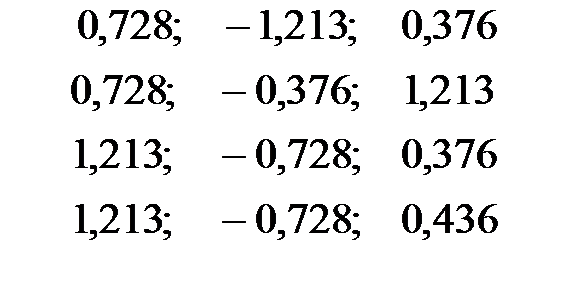
Стандартизованное уравнение регрессии имеет вид:
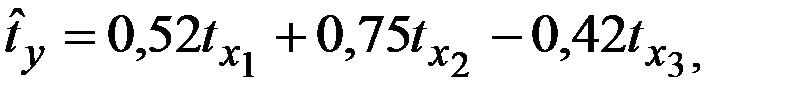
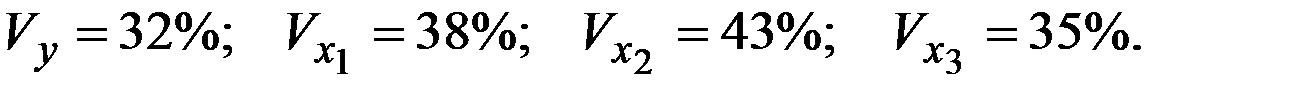
| + |
Частные коэффициенты эластичности равны:
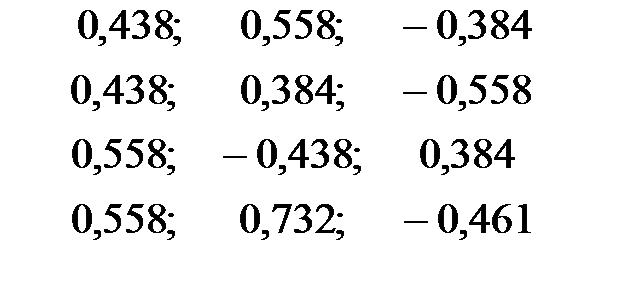
Стандартизованное уравнение регрессии имеет вид:
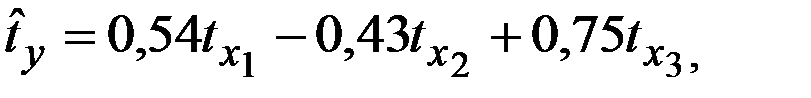
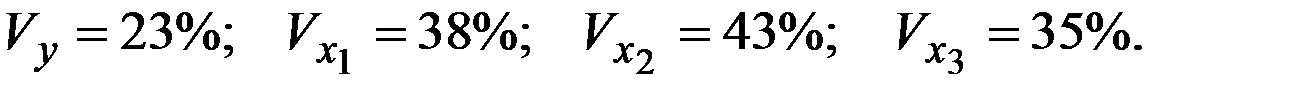
Частные коэффициенты эластичности равны:
| + |
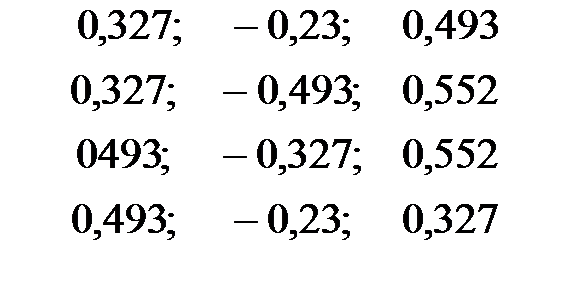
По 18 наблюдениям получены следующие данные:
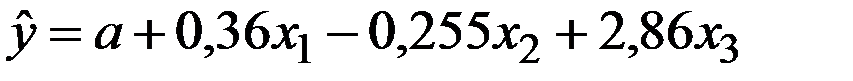
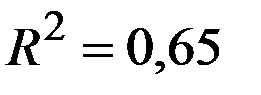 ;
; 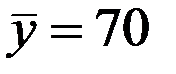 ;
; 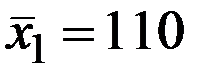 ;
; 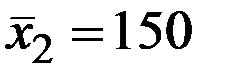 ;
; 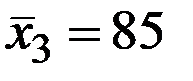
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 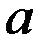 равны:
равны:
+— 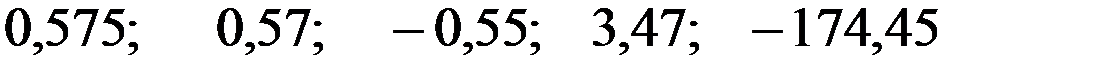
— 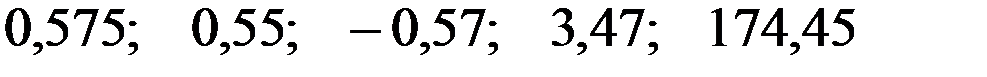
— 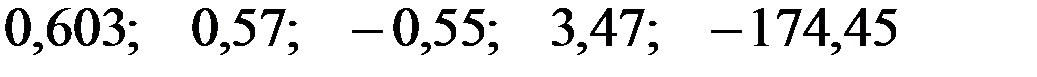
— 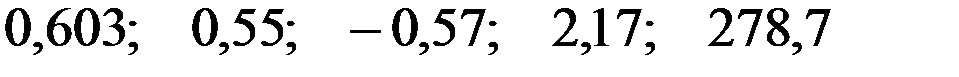
По 17 наблюдениям получены следующие данные:
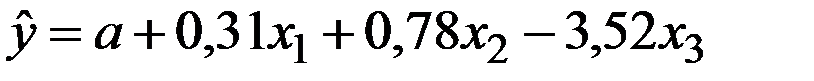
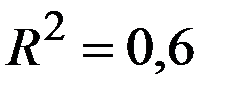 ;
; 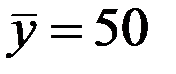 ;
;  ;
; 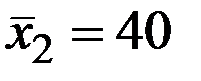 ;
; 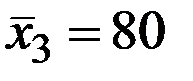
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 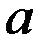 равны:
равны:
+— 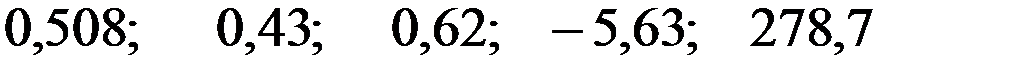
— 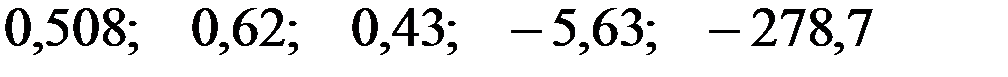
— 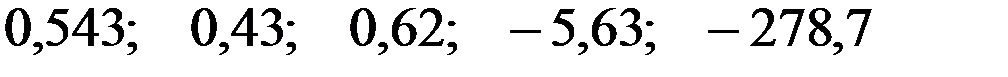
— 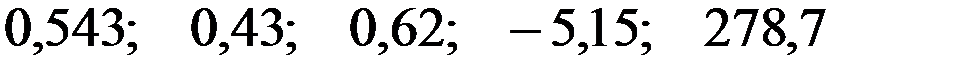
По 22 наблюдениям получены следующие данные:
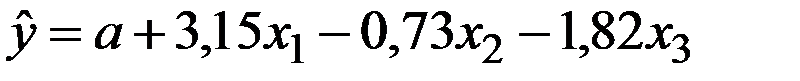
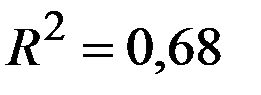 ;
; 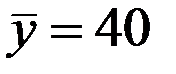 ;
; 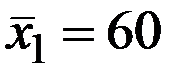 ;
; 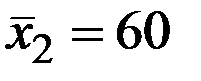 ;
; 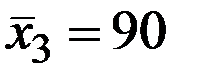
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 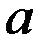 равны:
равны:
+— 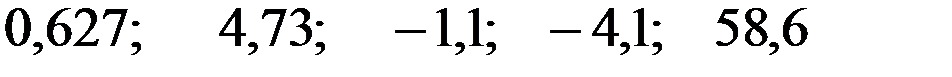
— 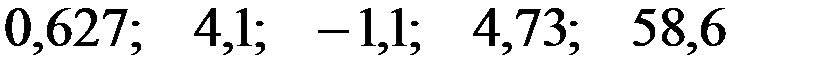
— 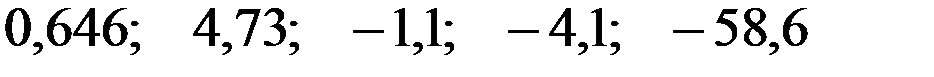
— 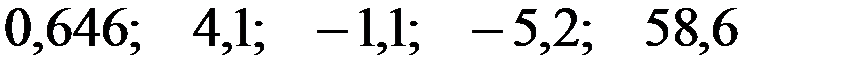
По 25 наблюдениям получены следующие данные:
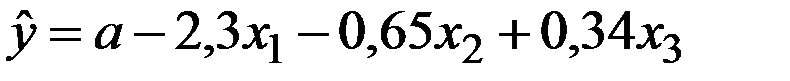
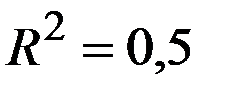 ;
; 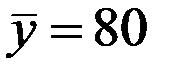 ;
; 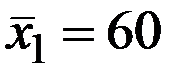 ;
; 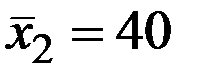 ;
; 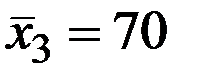
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 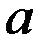 равны:
равны:
+— 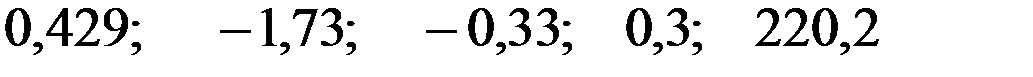
— 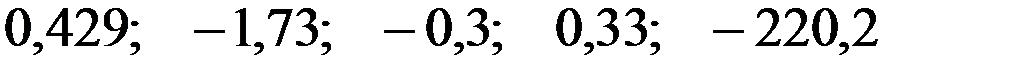
— 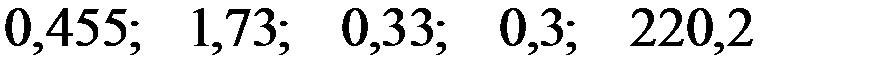
— 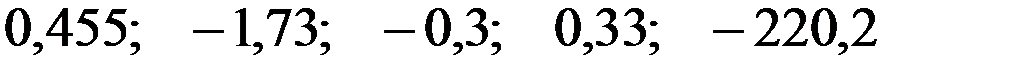
По 24 наблюдениям получены следующие данные:
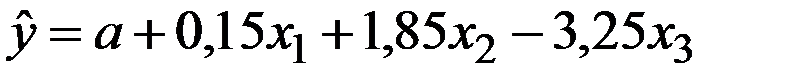
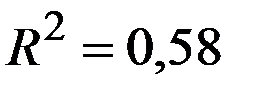 ;
; 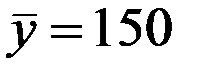 ;
; 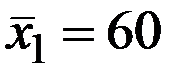 ;
; 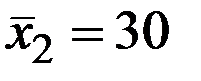 ;
; 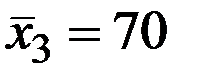
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 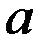 равны:
равны:
+— 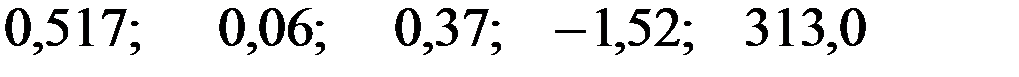
— 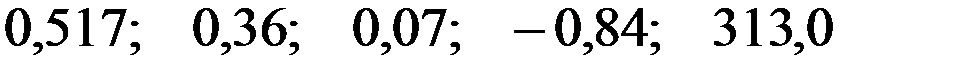
— 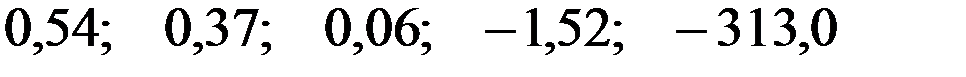
— 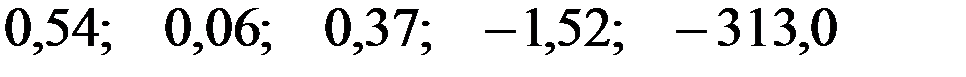
По 28 наблюдениям получены следующие данные:
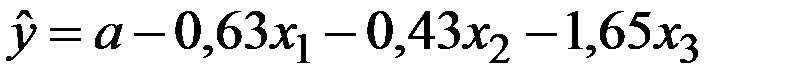
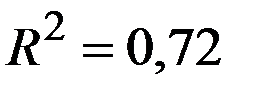 ;
; 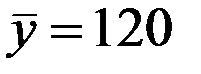 ;
; 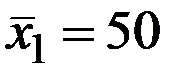 ;
; 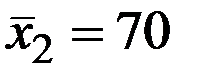 ;
; 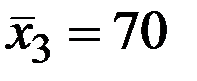
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 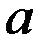 равны:
равны:
+— 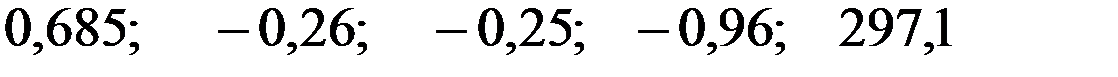
— 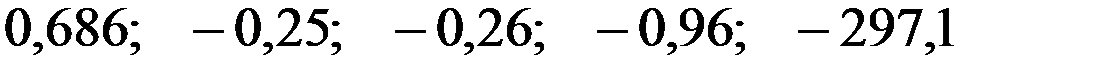
— 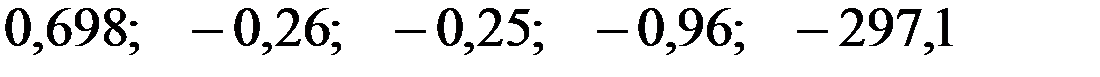
— 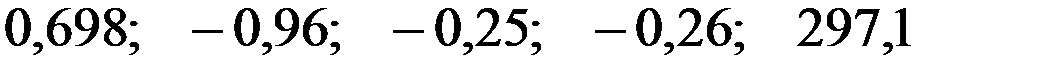
По 26 наблюдениям получены следующие данные:
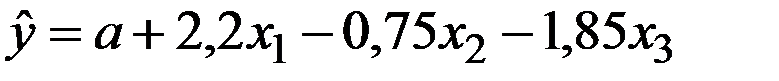
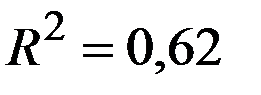 ;
; 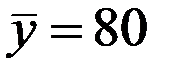 ;
; 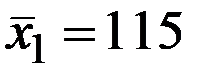 ;
; 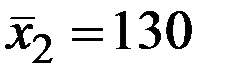 ;
; 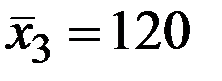
Значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра 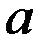 равны:
равны:
+— 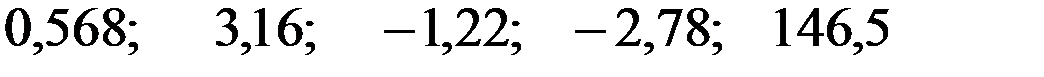
— 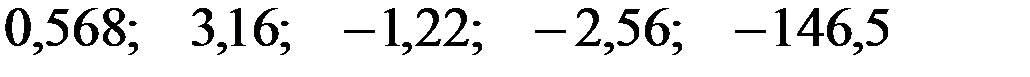
— 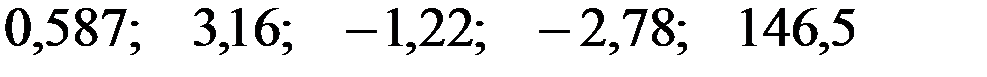
— 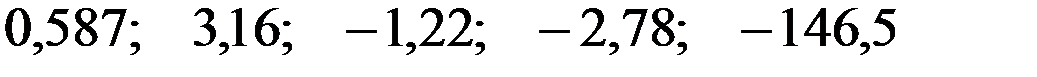
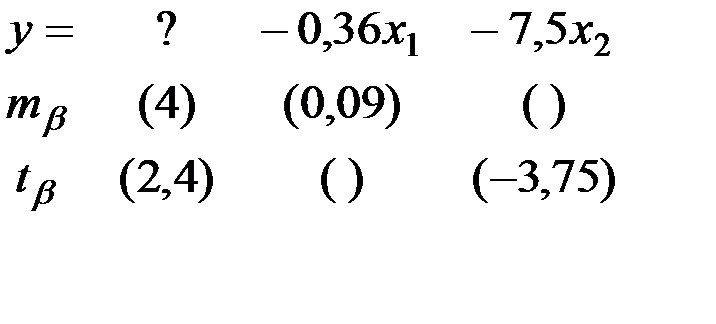
Восстановить пропущенные характеристики; построить доверительный интервал для 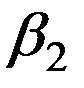 с вероятностью 0,95, если n=12
с вероятностью 0,95, если n=12
+— 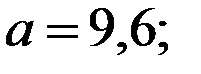
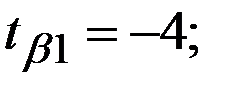
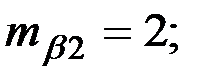 (-12,02;-2,98)
(-12,02;-2,98)
— 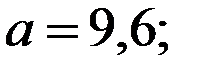
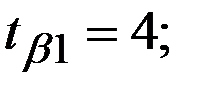
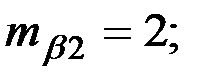 (-12,02;-2,98)
(-12,02;-2,98)
— 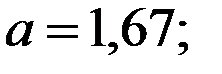
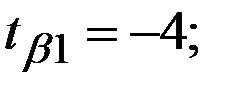
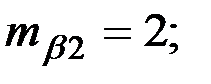 (-11,12;-3,88)
(-11,12;-3,88)
— 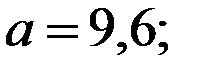
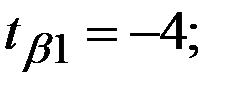
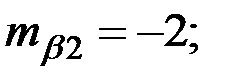 (-11,12;-3,88)
(-11,12;-3,88)
Уравнение регрессии в стандартизованном виде имеет вид:
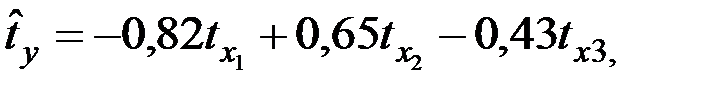
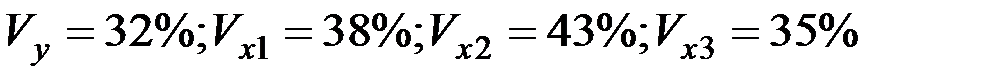
Как влияют факторы на результат и каковы значения частных коэффициентов эластичности?
+— Наибольшее влияние на результат оказывает фактор 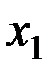 , наименьшее
, наименьшее 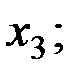
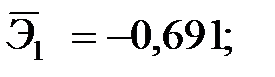
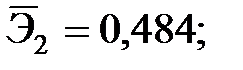
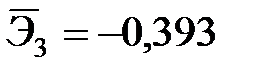
— Наибольшее влияние на результат оказывает фактор 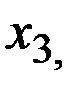 наименьшее -
наименьшее - 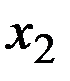 ;
; 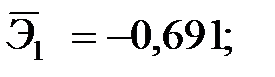
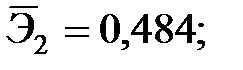
|
|
 2015-05-18
2015-05-18 47666
47666
