2015-06-16
2829
1.3.1. Абсолютные и относительные показатели
Абсолютные и относительные величины являются обобщающими показателями, характеризующими количественную сторону общественных явлений.
Абсолютные величины — именованные числа, имеющие опреде-
ленную размерность и единицы измерения. Они характеризуют по-
казатели на момент времени или за период. В зависимости от раз-
личных причин и целей анализа применяются натуральные, услов-
но-натуральные, денежные и трудовые единицы измерения.
Относительные величины характеризуют количественное соотношение сравниваемых абсолютных величин.
Числитель - сравниваемая величина, знаменатель называют базой сравнения или основанием сравнения. Как правило, базу сравнения принимают равной 1, 100, 1000, 10 000. Если основание равно 1, то относительная величина показывает, во сколько раз текущая величина больше базисной или какую долю от базисной она составляет, и выражается в коэффициентах. Если база сравнения равна 100, то относительная величина выражена в процентах (%), если база сравнения равна 1000 — в промилле (%о), 10 000 — в продецимилле (%оо).
Относительные показатели планового задания (ОППЗ) — отношение уровня, запланированного на предстоящий период (П), к уровню показателя, достигнутого в предыдущем периоде (Фо).
Относительный показатель выполнения плана (ОПВП) — отношение фактически достигнутого уровня в текущем периоде (Ф к) к уровню планируемого показателя на этот же период (П).
Относительные показатели динамики характеризуют изменение уровня развития какого-либо явления во времени.
Относительные показатели структуры характеризуют состав изучаемой совокупности, доли, удельные веса элементов совокупности в общем итоге и представляют собой отношение части единиц совокупности ко всему объему совокупности.
Относительные показатели интенсивности характеризуют сте-
пень насыщенности или развития данного явления в определенной
среде, являются именованными показателями и могут выражаться в
кратных отношениях.
Относительные показатели сравнения (ОПС) характеризуют отношения одноименных абсолютных показателей, соответствующих одному и тому же периоду или моменту времени, но к различным объектам или территориям.
1.3.2. Методы расчета средних величин и показателей вариации.
Средняя величина – это обобщающая характеристика однородной совокупности явлений по определенному признаку. Все многообразие средних величин и способы их расчета можно представить в виде схемы (рис.2).
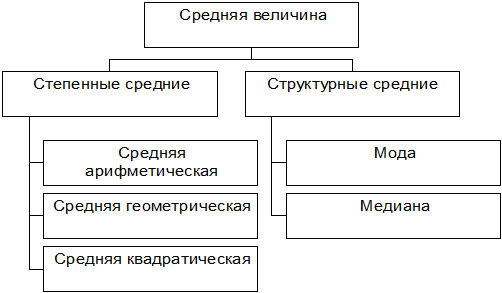
Рис.2. Виды средних величин
Средняя арифметическая простая и взвешенная применяется, если имеется несколько различных индивидуальных значений одного и того же признака.
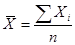(1) или 
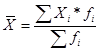(2)
Формула (1) применяется для несгруппированных данных, формула (2) для сгруппированных.
Средняя геометрическая применяется, если необходимо определить среднее значение коэффициентов (темпов) роста, если данные представлены в виде геометрической прогрессии.
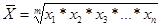, где
х I – коэффициенты (темпы) роста.
Средняя квадратическая рассчитывается в случаях, когда осреднению подлежат величины, выраженные в виде квадратных функций.
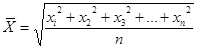
Мода – значение признака, наиболее часто встречающегося в исследуемой совокупности. Для интервальных вариационных рядов мода определяется в 2 этапа:
1) определение модального интервала – интервала с наибольшей частотой;
2) определение моды по формуле:
Мо = Хмо + iмо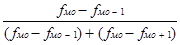 
, где
Хмо - нижняя граница модального интервала;
iмо – величина модального интервала;
fмо – частота модального интервала;
fмо-1 – частота интервала, предшествующего модальному;
fмо+1 – частота интервала, следующего за модальным.
Медиана – значение признака, приходящееся на середину ранжированной совокупности.
Определение медианы осуществляется в 2 этапа:
1) Нахождение медианного интервала. Для определения медианного интервала необходимо подсчитать накопленные частоты ряда. Медианным является интервал, которому соответствует накопленная частота, превышающая полусумму частот ряда, а предыдущая накопленная частота должна быть меньше полусуммы частот ряда.
2) Медиана интервального ряда распределения определяется по формуле:
Ме = Хме + iм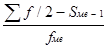е 
, где
Хме – нижняя граница значения интервала, содержащего медиану;
iме – величина медианного интервала;
Σf – сумма частот ряда распределения;
Sме-1 – сумма накопленных частот, предшествующих медианному интервалу;
ƒме - частота медианного интервала.
Вариация – это изменение значений какого-либо признака у отдельных единиц статистической совокупности в один и тот же момент времени.
Величина вариации признака в статистической совокупности характеризует ее однородность.
В статистической практике для изучения и измерения вариации используются следующие показатели:
· размах вариации (R)
R = Xmax – Xmin,
где Xmax – наибольшее значение варьирующего признака;
Xmin – наименьшее значение признака.
· среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признака от их средней.
= 
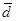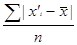, - если данные представлены в виде отдельных
значений признака (несгруппированы).
= 
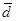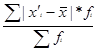, в случае наличия частот в ряду распределения,
где n – число единиц наблюдения
fi – частота интервала
x`i – среднее значение в интервале вариационного ряда
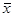- общая средняя ряда
· дисперсия (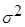
) - представляет собой средний квадрат отклонений индивидуальный значений признака от их средней величины.
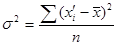- в случае отсутствия частот
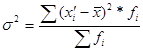- в случае наличия частот
· среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от из средней:
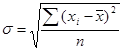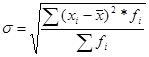или 
или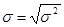 
· коэффициент осцилляции
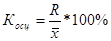, характеризует отклонение крайних значений признака от среднего значения.
· относительное линейное отклонение
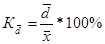, характеризует отклонение среднего линейного отклонения от средней.
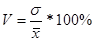, если V>33 %, статистическая совокупность является неоднородной, т. е. средняя нетипична и необъективна.
Контрольные вопросы:
1. Относительные показатели, их виды. Примеры расчета.
2. Виды средних величин. Способы их расчета.
3. Вариация массовых явлений. Показатели вариации.
1.3.3. Выявление трендов и циклов. Моделирование и прогнозирование развития социально-экономических процессов.
Ряд динамики – это данные, расположенные в хронологической последовательности. Ряд динамики состоит из двух элементов:
2 моменты или периоды времени, к которым относятся приводимые статистические данные;
3 статистический показатель, характеризующий изучаемый объект (уровень ряда).
Для характеристики особенностей и закономерностей развития изучаемого объекта рассчитывается система показателей:
· базисные и цепные показатели;
· абсолютные, относительные и средние показатели динамики.
Базисные показатели характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i - го) периода.
Цепные показатели характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
Абсолютные показатели ряда динамики:
· абсолютный прирост (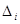
) - определяется как разность между двумя уровнями динамического ряда и показывает на сколько данный уровень ряда превышает уровень, принятый за базу сравнения:
а) базисный абсолютный прирост:
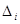= yi – y0; где
yi – уровень сравниваемого периода,
y0 – уровень базисного периода
б) цепной абсолютный прирост:
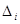= yi – yi-1; где
yi -1 – уровень непосредственно предшествующего периода.
Относительные показатели:
· темп роста – определяется как отношение двух сравниваемых уровней, выражается в процентах.
а) базисный темп роста
Тр =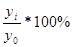 
б) цепной темп роста
Тр =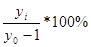 
· темп прироста – показывает на сколько процентов уровень данного периода больше (меньше) базисного уровня.
Рассчитывается двояко:
1) как отношение абсолютного прироста к уровню, принятому за базу сравнения.
Тn =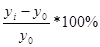 
или Тn =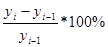 
2) как разность между темпом роста (в %) и 100%
Тn = Тр – 100%
· абсолютное значение 1 % прироста – рассчитывается как отношение абсолютного прироста к темпу прироста (в %) за тот же период времени
Ai =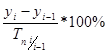 
или Ai =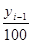 
Средние показатели:
· средний уровень ряда (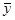
)
Метод расчета среднего уровня ряда динамики зависит от вида временного ряда.
Для интервального ряда динамики:
,
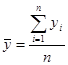где n – число уровней ряда.
Для моментного ряда динамики:
а) моментный ряд с равными промежутками времени
,
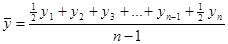где n – число дат (моментов времени)
б) моментный ряд с неравными промежутками времени
,
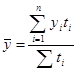где ti – количество дней (месяцев) между смежными датами.
· Средний абсолютный прирост (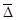
) – рассчитывается как средняя арифметическая абсолютных приростов за отдельные промежутки времени
,
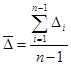где n – число уровней ряда
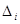- абсолютные изменения по сравнению с предшествующим уровнем.
· средний темп роста (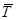
р) – вычисляется по формуле средней геометрической из показателей темпов роста за отдельные периоды
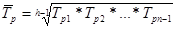или 
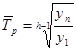, где
Тр1,… Трn-1 – темпы роста по сравнению с уровнем предшествующего периода;
n – число уровней ряда.
· Средний темп прироста (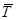 пр) – определяется как разность между средним темпом роста и 100 % и показывает на сколько процентов в среднем изменяются уровни рассматриваемого ряда динамики
·
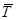пр = 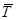р – 100 %
Основная тенденция ряда динамики называется трендом. Выявление основной тенденции ряда динамики или выравнивание ряда динамики осуществляется следующими способами:
Для определения скользящей средней формируют укрупненные интервалы, состоящие из одинакового числа уровней ряда. Каждый последующий интервал получают, постепенно двигаясь от начального уровня ряда динамики на один уровень. Тогда первый интервал будет включать уровни у1, у2, …, уm; второй – уровни у3, у4, …, уm+1 и т.д. По сформированным укрупненным интервалам определяют сумму значений уровней, на основе которых рассчитывают скользящие средние. Полученная средняя относится к середине укрупненного интервала. Поэтому при сглаживании скользящей средней удобнее укрупненный интервал составлять из нечетного числа уровней ряда (3, 5, 7 уровней).
б) Метод аналитического выравнивания.
Метод используется для того, чтобы представить количественную модель, выражающую общую тенденцию изменений уровней ряда динамики во времени. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной кривой, уровень изучаемого показателя оценивается как функция времени yt = ƒ(t), где yt - уровни ряда динамики, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Наиболее часто используемые трендовые модели для аналитического выравнивания:
Линейная уt = в0 + в1t
Парабола 2-го порядка уt = в0 + в1t + в 2t2
Кубическая парабола уt = в0 + в1t + в 2t2 + в 3t3
Показательная уt = в0 в1 t
Экспоненциальная уt = в0 l в1 t
Гипербола уt = в0 + в1 
Выбор формы кривой во многом определяет результаты экстраполяции тренда. Основанием для выбора вида кривой может использоваться содержательный анализ сущности развития данного явления, а также анализ графического изображения уровней ряда динамики, либо его сглаженных уровней (метод скользящей средней), в которых случайные и волнообразные колебания в некоторой степени оказываются погашенными.
При выборе вида кривой для выражения ряда динамики возможно также использование метода конечных разностей, заключающегося в следующем:
· если общая тенденция выражается линейным уравнением, то постоянными являются первые разности ∆`i = yi – yi-1, и нулевыми вторыми разностями ∆``i = ∆`i – ∆`i-1;
· если тенденция выражается параболой 2-го порядка, то постоянными являются вторые разности и нулевыми – третьи разности.
В общем виде правило можно сформулировать следующими образом: порядок разностей, остающихся примерно равными друг другу, принимается за степень выравнивания многочлена.
Параметры уравнения рассчитываются по методу наименьших квадратов (МНК). Для прямой система нормальных уравнений имеет вид:
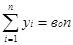
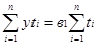, откуда
во =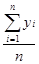 
; в1 =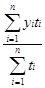 
Для параболы второго порядка:
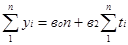
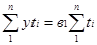
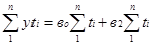
При условии, что ∑ti = 0. Для выполнения этого условия необходимо:
a) в случае нечетного числа уровней ряда. За условно начало отчета (t=0) принимается уровень, находящейся в середине ряда. Даты времени, стоящие выше этого уровня, обозначаются t = -1, -2, -3 и т. д., а ниже -t = +1, +2, +3 и т. д.
b) в случае четного числа уровней ряда. Периоды времени верхней половины ряда (до середины) нумеруются t = -1, -3, -5 и т. д., а нижней - t = +1, +3, +5 и т. д.
Используя полученное уравнение можно строить прогнозы на будущее в развитии изучаемого явления. Продление в будущее тенденции, наблюдавшейся в прошлом, носит название экстраполяции.
Контрольные вопросы:
1. Понятие о рядах динамики, их виды
2. Методы расчета показателей ряда динамики
3. Методы анализа основной тенденции развития в рядах динамики и прогнозирование
1.3.4. Индексы в экономическом анализе
Индекс – это относительная величина, которая характеризует изменение во времени или в пространстве уровня изучаемого явления.
Классификация индексов может быть представлена в виде схемы (рис.3).
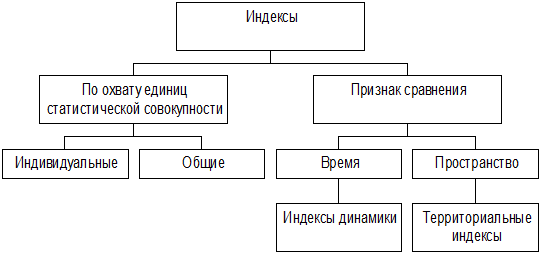
Рис.3. Классификация индексов
Индивидуальные индексы выражают соотношение отдельных элементов совокупности.
Например, индекс физического объема продукции:
iq = q1 / q 0,
где q0 и q1 – количество произведенной продукции в базисном и отчетном периодах.
Общие индексы показывают соотношение совокупности явлений, состоящих из разнородных, непосредственно несоизмеримых элементов.
Общий индекс состоит из двух элементов – индексируемой (изменяемой) величины и веса - соизмерителя (от влияния которой абстрагируемся).
Наиболее распространенной формой экономических индексов является агрегатная форма индекса, т.е. когда числители и знаменатели представляют собой суммы произведений уровней изучаемого явления.
Общий индекс физического объема продукции рассчитывается по формуле:
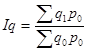(формула Ласпейреса);
Общий индекс цены рассчитывается по формуле:
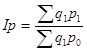(формула Пааше).
Общий стоимостной индекс рассчитывается по формуле:
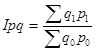
Основное правило индексного анализа:
1. Если оценивается изменение количественных показателей, необходимо использовать для расчетов формулу Ласпейреса (вес – соизмеритель фиксируется на уровне базисного периода).
2. Если оценивается изменение качественных показателей, необходимо использовать формулу Пааше (вес-соизмеритель фиксируется на уровне отчетного периода).
Агрегатные индексы цен, физического объема продукции и товарооборота могут быть вычислены при условии, если известны индексируемые величины и веса. Но в ряде случаев не располагают необходимыми данными, поэтому используют среднеарифметический и среднегармонический индексы.
Среднеарифметический индекс физического объема:
;
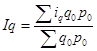Среднегармонический индекс цены:
.
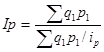В ряде случаев приходится изучать динамику общественных явлений, уровни которых выражены средними величинами (средней ценой, средней себестоимостью и т.д). Динамика средних показателей зависит от одновременного изменения вариантов, из которых формируются средние, и изменения удельных весов этих вариантов, т.е. от структуры изучаемого явления. Изучение совместного действия указанных факторов на общее изменение динамики среднего уровня явления, а также роли влияния каждого фактора в отдельности в общей динамике средней проводится в статистике с помощью индекса фиксированного состава, индекса переменного состава и индекса структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующее изменение индексируемого (осредняемого) показателя. Индекс переменного состава имеет следующий вид:
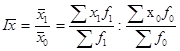
Величина этого индекса характеризует изменение средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного (фиксированного) состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя (х) у единиц совокупности. В общем виде он может быть записан следующим образом:
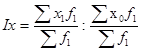
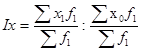
Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:
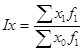
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:
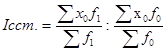
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d). Система взаимосвязанных индексов при анализе динамики среднего уровня качественного показателя имеет вид:
Ixср=Iх * Iстр
В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности (d = f/Sf), которые отражают изменения в структуре изучаемой совокупности.
Аналогично приведенным формулам строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производительности труда, оплаты труда и т.д.
Контрольные вопросы:
1. Общее понятие об индексах, их классификация.
2. Общие индексы количественных и качественных показателей
4. Территориальные индексы
1.4. Корреляционная связь и ее статистическое изучение
1.4.1. Парная корреляция и регрессия
Основоположником теории корреляции считаются английские ученые Ф.Гальтон и К.Пирсон. Термин «корреляция» означает соотношение, соответствие. В корреляционных связях между изменением экзогенной (фактора) и эндогенной (результатом) переменными нет полного соответствия, воздействие отдельных факторов проявляется лишь в среднем при массовом наблюдении фактических данных.
Различают парную и множественную корреляцию. В случае парной корреляции на результативный показатель оказывает влияние один фактор, в случае множественной – несколько факторов.
Зависимость между результативным и факторным показателями может носить как линейный, так и нелинейный характер. Этапами корреляционного анализа в случае линейной зависимости являются:
1. На основе законов экономической теории выдвигается гипотеза о наличии связи между показателями.
2. Сбор статистической информации. На данном этапе должны соблюдаться следующие требования:
1 Массовость данных – единиц наблюдения должно быть как минимум в 10 раз больше числа факторов.
2 Однородность статистической информации (исходная совокупность должна быть «очищена» от резко выделяющихся наблюдений) – коэффициент вариации меньше 33 %.
3. Дается оценка степени тесноты связи между результативным и факторным показателем. Для этих целей используется линейный коэффициент корреляции.
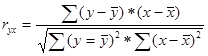
Коэффициент изменяется от 0 до 1. Знак коэффициента свидетельствует о направлении связи.
Для оценки результата можно использовать качественную оценку тесноты связи величин X и Y с помощью шкалы Чеддока:
| Значение коэффициента корреляции при наличии: | ||
| прямой связи | обратной связи | |
| Слабая | 0,1-0,3 | (-0,1)-(-0,3) |
| Умеренная | 0,3-0,5 | (-0,3)-(-0,5) |
| Заметная | 0,5-0,7 | (-0,5)-(-0,7) |
| Высокая | 0,7-0,9 | (-0,7)-(-0,9) |
| Весьма высокая | 0,9-0,99 | (-0,9)-(-0,99) |
4. Строится математическая модель зависимости между результативным и факторным признаками (уравнение регрессии).
Уравнение линейной регрессии имеет вид:
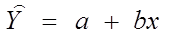
Параметры а и b уравнения определяются методом наименьших квадратов. После решения системы нормальных уравнений получим формулы для определения этих параметров:
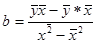(1)
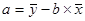(2)
5. Дается оценка значимости (адекватности) полученного уравнения. Для этой цели рассчитываются и оцениваются следующие параметры:
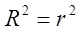(3)
Он показывает, какая доля вариации результата объясняется вариацией фактора. Модель может считаться значимой, если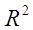 
> 0,5.
2 F- критерий Фишера. Расчетное значение критерия определяется по формуле:
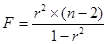(4)
Уравнение считается значимым, если выполняется неравенство:
Fрасч > F табл (для α = 0,05 k1 = m, k2 = n – m – 1). Fтабл определяется по таблицам Фишера, где m – число факторов в уравнении регрессии (в случае парной корреляции m = 1), n – число единиц наблюдений.
· Средняя относительная ошибка (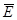
), характеризующая насколько расчетные значения отличаются от фактических, полученных в результате наблюдения.
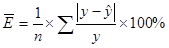(5)
Модель считается значимой, если относительная ошибка меньше 20%.
Особенностью исследования в случае нелинейной зависимости является порядок следования этапов.
Этап 3. Построение модели нелинейной зависимости. Для построения моделей используется следующий прием – производят линеаризацию моделей с помощью логарифмирования обеих частей уравнения.
Рассмотрим пример построения моделей нелинейной регрессии.
1. Построение степенной модели парной регрессии
Уравнение степенной модели имеет вид:
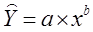
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
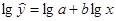
Обозначим Y = lgy, X = lgx, A= lga.
Тогда уравнение примет вид: Y= А + b X – линейное уравнение регрессии. Параметры уравнения А и b определяются по формулам (1) и (2).
Переход к исходным переменным х и у осуществляется потенцированием полученного уравнения. Например, уравнение регрессии будет иметь вид: Y = -0.548 + 1.254 X, тогда исходное уравнение:
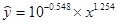
2. Построение показательной функции
Уравнение показательной кривой:
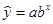
После логарифмирования имеем:
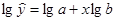
Обозначим Y = lgy, В = lgb, A= lga.
Тогда уравнение примет вид: Y= А + B x – линейное уравнение регрессии.
3. Построение гиперболической функции
Уравнение гиперболической функции: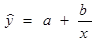 
Произведем линеаризацию модели путем замены Х = 1/х.
В результате получим линейное уравнение у = а + bХ. Для перехода к исходным параметрам необходимо произвести обратную замену Х = 1/х.
Этап 4. Определение степени тесноты связи между У и Х. Для этих целей в случае нелинейных зависимостей используется индекс корреляции:
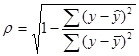(6)
Данный показатель изменяется от 0 до 1 (всегда положительный, не характеризует направление связи), для качественной оценки степени тесноты связи может применяться шкала Чеддока.
Параметры значимости нелинейных моделей (этап 5) те же самые, что и в случае линейной регрессии.
1.4.2.. Прогнозирование с применением уравнения регрессии
Регрессионные модели могут быть использованы для прогнозирования возможных ожидаемых значений зависимой переменной.
Прогнозируемое значение переменной У получается при подстановке в уравнение регрессии ожидаемой величины фактора Х, например, для линейной модели:
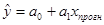
Данный прогноз называется точечным. Вероятность реализации точечного прогноза практически равна нулю. Поэтому рассчитывается средняя ошибка прогноза или доверительный интервал прогноза с достаточно большой надежностью.
Доверительные интервалы зависят от стандартной ошибки удаления Хпрогн от своего среднего значения Х, количества наблюдений n и уровня значимости прогноза α.
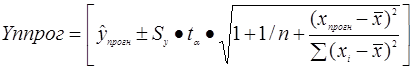(7)
Величину отклонения от линии регрессии вычисляют по формуле:
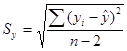(8)
1.4.3.. Непараметрические методы оценки степени тесноты связи
Для оценки степени тесноты связи между количественными признаками, форма распределения которых отличается от нормальной, а также между качественными признаками прибегают к непараметрическим методам. В основу непараметрических методов положен принцип нумерации значений статистического ряда. Каждой единице совокупности присваивается порядковый номер в ряду, который будет упорядочен по уровню признака. Таким образом, ряд значений признака ранжируется, а номер каждой отдельной единицы будет ее рангом.
Можно получить предварительное представление о наличии или отсутствии связи между признаками, если сопоставить последовательность взаимного расположения рангов факторного и результативного признаков. Для этого ранги индивидуальных значений факторного признака располагают в порядке возрастания, и если ранги результативного признака обнаруживают тенденцию к увеличению, можно предполагать наличие прямой связи; если же с увеличением рангов факторного признака ранги результативного признака уменьшаются, то это свидетельствует о возможном наличии между изучаемыми признаками обратной связи.
Коэффициенты корреляции, основанные на использовании рангов, были предложены К. Спирмэном и М.Кендэлом.
Коэффициент корреляции рангов Спирмэна (был использован им вначале XX в.) основан на рассмотрении разности рангов значений факторного и результативного признаков.
Формула для расчета выглядит следующим образом:
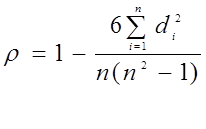(9)
Поскольку коэффициенты корреляции рангов могут изменяться в пределах от -1 до +1 (как и линейный коэффициент корреляции), по результатам расчетов коэффициента Спирмэна можно предположить наличие достаточно тесной прямой зависимости меду оценками экспертов на стадии предвыборной компании и результатами выборов. Однако нельзя не учесть то обстоятельство, что ранговый коэффициент был рассчитан по небольшому объему исходной информации (п=10). Не является ли отличие рангового коэффициента от нуля лишь результатом случайных совпадений оценок экспертов с результатами выборов по данным малого числа отобранных депутатов, можно ли распространить полученные выводы на генеральную совокупность?
Для совокупностей небольшого объема (л <30) распределение рангового коэффициента корреляции не является нормальным и нецелесообразно использовать значения t по нормированной функции Лапласа для проверки гипотезы о величине рангового коэффициента корреляции. В Приложении
приводится таблица предельных значений коэффициентов корреляции рангов Спирмэна при условии верности нулевой гипотезы об отсутствии корреляционной связи при заданном уровне значимости и определенном объеме выборочных данных.
М.Кендэл предложил еще одну меру связи между переменными х и у - коэффициент корреляции рангов Кендэла–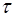 
.
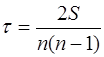(10)
где S = P+Q.
Для вычисления т надо упорядочить ряд рангов переменной х, приведя его к ряду натуральных чисел. Затем рассматривают последовательность рангов переменной у.
Для нахождения суммы S (формула 10) находят два слагаемых Р и О. При определении слагаемого Р нужно установить, сколько чисел, находящихся справа от каждого из элементов последовательности рангов переменной у, имеют величину ранга, превышающую ранг рассматриваемого элемента.
Второе слагаемое О характеризует степень несоответствия последовательности рангов переменной у последовательности рангов переменной х
Коэффициент Кендэла также изменяется в пределах от -1 до + 1 и равен нулю при отсутствии связи между рядами рангов.
При достаточно большом числе наблюдений между коэффициентами корреляции рангов Спирмэна и коэффициентом корреляции рангов Кендэла существует следующее соотношение:
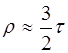. (11)
Существенность коэффициента корреляции рангов Кендэла проверяется при уровне значимости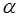 
по формуле
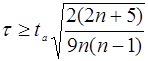(12)
Для оценки степени тесноты связи между несколькими признаками при использовании ранговой корреляции применяется коэффициент конкордации, который вычисляется по формуле:
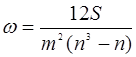(13)
где т - число факторов;
п - число ранжируемых единиц;
S - сумма квадратов отклонений рангов.
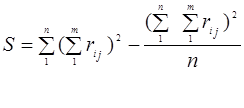(14)
При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативного признака, используют коэффициент ассоциации или коэффициент контингенции
Коэффициент ассоциации (КА) определяется по формуле
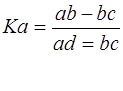(15)
В тех случаях, когда хотя бы один из четырех показателей в таблице «четырех полей» отсутствует, величина коэффициента ассоциации будет равна единице, что дает преувеличенную оценку степени тесноты связи между признаками, и предпочтение следует отдать коэффициенту контингенции (Кк):
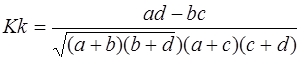(16)
1.4.4. Множественная регрессия и корреляция.
Линейная модель множественной регрессии имеет вид:
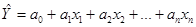
Коэффициент регрессии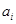 
показывает, на какую величину в среднем измениться результативный признак У, если переменную 
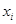увеличить на единицу измерения, т.е. 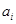является нормативным коэффициентом.
Рассмотрим этапы построения модели множественной регрессии с помощью пакета EXCEL (пункт меню СЕРВИС – АНАЛИЗ ДАННЫХ).
1. Анализ степени тесноты связи между У и каждым из 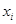, а также между факторами :
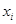· Режим КОРРЕЛЯЦИЯ позволяет получить матрицу парных коэффициентов корреляции. Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных (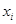). Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели. Считают явление мультиколллинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.
2. Построение модели множественной регрессии режим РЕГРЕССИЯ:
1 В поле Входной интервал У введите адрес одного диапазона ячеек, котрый представляет зависимую переменную. В поле Входной интервал Х введите адреса одного или нескольких диапазонов, котрые содержат значения независимых переменных;
2 Если выделены и заголовки столбцов, то установите флажок Метки в первой строке;
3 Выберите параметры выводы (например, Новая рабочая книга);
4 В поле Остатки поставьте необходимые флажки.
3. Результат регрессионного анализа представляется в виде:
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика Таблица 1 | ||||||
| Множественный R | 0,827970491 | |||||
| R-квадрат | 0,685535134 | |||||
| Нормированный R-квадрат | 0,595688029 | |||||
| Стандартная ошибка | 12,03169377 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | Таблица 2 | |||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 2209,068415 | 1104,534207 | 7,630019198 | 0,017438232 | ||
| Остаток | 1013,331585 | 144,7616551 | ||||
| Итого | 3222,4 | |||||
| Таблица 3 | ||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | -18,165 | 20,0982 | -0,9038 | 0,3961 | -65,689 | 29,35978 |
| Переменная X 1 | 0,6392 | 0,47613 | 1,3426 | 0,2212 | -0,4866 | 1,765174 |
| Переменная X 3 | 0,6706 | 0,38549 | 1,7397 | 0,1254 | -0,2408 | 1,582205 |
Пояснения результатов:
| № | Наименование в EXCEL | Наименование | Комментарий |
| Множественный R | Коэффициент множественной корреляции | Характеризует степень тесноты связи между У и факторами Хi | |
| R-квадрат | Коэффициент детерминации | Показывает какая доля вариации результативного показателя объясняется вариацией факторов, включенных в модель. Чем ближе к 1, тем лучше качество модели | |
| Нормированный R-квадрат | Скорректированный R2 | Коэффициент детерминации, скорректированный с учетом числа независимых переменных | |
| Стандартная ошибка | Стандартная ошибка оценки | Средний квадрат отклонений фактических значений У от расчетных значений, полученных по уравнению регрессии | |
| Наблюдения | Количество наблюдений, n | Количество единиц наблюдения | |
| df | Число степеней свободы, k | Число факторов в модели | |
| SS | Сумма квадратов | Сумма квадратов отклонений расчетных значений от средних фактических | |
| MS | Среднее значение | Среднее значение п.7 | |
| F | F- критерий Фишера (расчетное значение) | Используется для оценки значимости полученного уравнения |
Во втором столбце последней таблицы результатов (табл.3) представлены коэффициенты уравнения регрессии а0, а1 и т.д. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии, а в четвертом – t- статистика (табличное значение), используемая для проверки значимости коэффициентов уравнения регрессии.
4. Оценка качества модели
Оценка качества модели производится с помощью следующих критериев:
1 Коэффициент детерминации;
2 F- критерий Фишера. Табличное значение F-критерия при заданном уровне значимости α и v 1 = k – число факторов в модели; и v2 = n – k – 1 находится по таблице Фишера. Если Fрасч >F табл, делается вывод о значимости полученного уравнения.
3 t- критерий Стьюдента. Позволяет оценить значимость коэффициентов уравнения множественной регрессии. Табличное значение критерия находится по таблицам Стьюдента для заданного α и v = n – k – 1 степеней свободы. Если tрасч >t табл, коэффициент регрессии является значимым. В противном случае незначимый фактор должен быть исключен из модели и построение модели повторяется с п. 2. В случае незначимости нескольких факторов процедура исключения повторяется в пошаговом режиме (все факторы сразу не удаляются). Значимой считается модель со значимыми факторами.
15. Статистическая методология национального счетоводства и макроэкономических расчетов.
Система национальных счетов – современная система информации, используемая для описания развития экономики страны на макроуровне. Наиболее важные макроэкономические показатели:
1 валовой внутренний продукт (ВВП);
2 валовой национальный доход (ВНД);
3 валовой национальный располагаемый доход (ВНРД);
4 валовое накопление;
5 валовое сбережение.
Валовой внутренний продукт (ВВП) – стоимость товаров и услуг, произведенных резидентами страны за тот или иной период. ВВП исчисляется в рыночных ценах конечного потребления. ВВП на стадии производства рассчитывается как сумма валовой добавленной стоимости всех отраслей и секторов экономики.
ВВП = SВДС,
В рыночных ценах:
ВВП = SВДС + ЧНП + ЧНИ,
Где ВДС – валовая добавленная стоимость;
ЧНП – чистые налоги на продукты;
ЧНИ – чистые налоги на импорт.
ВВП на стадии образования доходов рассчитывается:
ВВП = ОТ + ЧНП + ЧНИ + ДНП + ВПЭ, где
От – оплата труда наемных работников;
ДНП – другие налоги на производство;
ВПЭ – валовая прибыль экономики.
Валовая прибыль экономики – характеризует превышение доходов над расходами, которые предприятия имеют в результате производства до вычета явных или скрытых процентных издержек, арендной платы или других доходов от собственности.
ВПЭ = ВДС – ОТ – ДНП
Чистая прибыль экономики – рассчитывается путем вычитания потребления основного капитала (ПОК) из валовой прибыли экономики:
ЧПЭ = ВПЭ – ПОК.
Потребление основного капитала представляет собой уменьшение стоимости основного капитала в течение отчетного периода в результате его физического и морального износа, случайных повреждений.
Валовой внутренний продукт на стадии конечного использования рассчитывается как сумма конечного потребления материальных благ и услуг (КПМБ), валового накопления (ВН) и чистого (за вычетом импорта) экспорта товаров и услуг плюс статистическое расхождение:
ВВП = КПМБ + ВН + ЧЭ + СР, где
ЧЭ – чистый экспорт (за вычетом импорта);
СР – статистическое расхождение между произведенным и использованным ВВП.
Валовой национальный доход (ВНД) -рассчитывается как сумма ВВП в рыночных ценах плюс доходы от собственности, полученные от «остального мира», минус соответствующие им потоки, переданные «остальному миру».
ВНД = ВВП - SПД
Располагаемый доход образуется в результате распределения и перераспределения доходов и предназначен для конечного потребления и сбережения.
Располагаемый национальный доход (РНД) в рыночных ценах представляет собой чистый национальный доход плюс чистые текущие трансферты из-за границы (дарения, пожертвования, гуманитарная помощь, а также аналогичные перераспределительные поступления из-за границы за вычетом аналогичных трансфертов, переданных за границу).
Валовой располагаемый доход (ВРД) равен ВНД в рыночных ценах плюс (минус) текущие трансферты, полученные от «остального мира» и переданные «остальному» миру.
Чистый располагаемый доход (ЧРД) представляет собой разность между ВРД и потреблением основного капитала.
Валовое сбережение - сбережение до вычета потребления основного капитала, равное сумме валовых сбережений всех секторов экономики.
Валовое накопление -валовое накопление основного капитала, изменение запасов материальных оборотных средств и чистое приобретение ценностей.
Контрольные вопросы:
1. Понятие о системе национальных счетов.
2. Основные макроэкономические показатели СНС, способы их расчета.
1.6. Статистический анализ эффективности функционирования предприятий разных форм собственности, качества продуктов и услуг.
Эффективность функционирования предприятия может быть охарактеризована следующими показателями:
2 оборачиваемости активов;
3 прибыльность.
Ликвидность предприятия определяется системой показателей:
Коэффициент абсолютной ликвидности определяют как отношение наиболее ликвидных активов (денежные средства и краткосрочные финансовые вложения) к краткосрочным обязательствам предприятия (краткосрочные ссуды, кредиторская задолженность). Нормативное значение – >0,2.
Коэффициент быстрой ликвидности определяют как отношение быстрореализуемых активов (денежные средства, отгруженные товары, дебиторская задолженность) к краткосрочным обязательствам. Нормативное значение – 0.7-1.0
Коэффициент текущей ликвидности (покрытия) определяется как отношение всех ликвидных активов к краткосрочным обязательствам. Нормативное значение >=2.
Оборачиваемость активов может быть охарактеризована с помощью следующих показателей:
Коэффициент оборачиваемости всех активов:
Ка = О / А, где
О – объем реализации продукции;
А – среднегодовая стоимость активов.
Коэффициент оборачиваемости оборотных активов:
Ко = О / Ао, где
Ао – среднегодовая стоимость оборотных активов;
Продолжительность 1 оборота в днях:
Об = Ао х Д / О, где
Д – количество дней в периоде.
Размер высвобождения (дополнительной загрузки) оборотных средств в результате ускорения (или замедления) оборачиваемости оборотных средств:
Ао высв = Ао – Т0 х Оф /Д, где
Т0 –продолжительность одного оборота средств в базисном периоде;
Оф – объем реализации в отчетном периоде;
Фондоотдача:
ФО = О / ОФ, где
ОФ – среднегодовая стоимость основных средств.
Фондоотдача характеризует эффективность использования основных фондов предприятия и показывает, какой объем продукции приходится на 1 рубль основных фондов.
Прибыль от реализации продукции определяется как разница между выручкой от реализации продукции и затратами на ее производство.
Пр = S(p – z) х q, где
p – цена единицы продукции;
z – затраты на производство единицы продукции;
q – объем продукции.
